Исленное моделирование электродинамических устройств на базе пакета Ansoft HFSS. Метод конечных элементов в решении задач прикладной электродинамики

Метод конечных элементов в решении задач прикладной электродинамики

Решение трехмерных и двумерных задач электродинамики в пакете  HFSS базируется на методе конечных элементов (Finite Element Method) (МКЭ). Метод предусматривает разбиение исследуемой области на систему  объемных элементов, имеющих форму тетраэдров. Размер тетраэдра должен быть достаточно мал для того, чтобы поле в его пределах можно было описать простой функцией или набором функций с неизвестными коэффициентами. Эти коэффициенты ищутся из сиcтемы уравнений Максвелла и соответствующих решаемой задаче граничных условий. В результате электродинамическая задача сводится к системе линейных алгебраических уравнений (СЛАУ) относительно этих коэффициентов. Сильная разреженность СЛАУ позволяет использовать для их решения эффективные численные методы.

Пример декомпозиции отрезка прямоугольного волновода на  систему тетраэдров показан на рис. 1.

При решении двумерных задач, в качестве элемента декомпозиции используется двумерный аналог тетраэдра – треугольник, как показано на рис. 2.

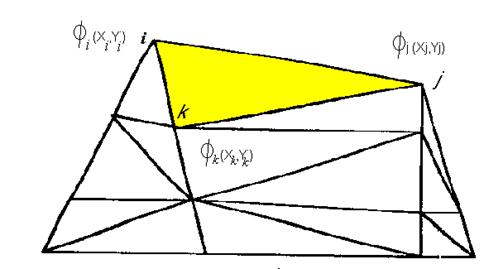
Рис. 2. Разбиение области на систему двумерных элементов.

Для простоты рассмотрим особенности алгоритма, реализующего метод конечных элементов, на примере двумерной электростатической задачи.

Пусть требуется найти потенциал электростатического поля в области, показанной на рис. 3.

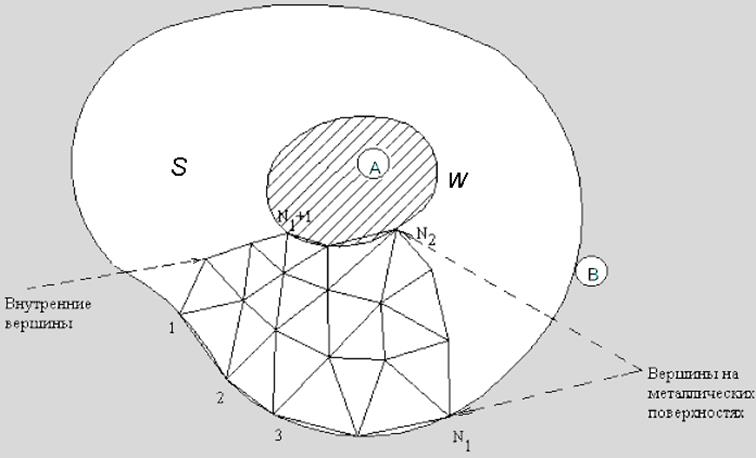
Рис. 3. Исследуемая структура.

Анализируемая структура состоит из двух металлических проводников: внешнего и внутреннего (А и В). Пространство между проводниками заполнено воздухом. Такая структура может служить моделью коаксиальной линии с проводниками со сложным поперечным сечением. Поле в поперечном сечении коаксиальной линии подчиняется уравнению Лапласа 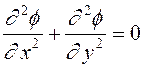. В электростатике принято выражать поле через электростатический потенциал , являющийся функцией двух координат х и у. Известно, что потенциал поля на поверхности проводника является постоянной величиной. Поэтому можно положить, что потенциал внешнего проводника равен нулю, а внутреннего некоторой величине W.

На рис. 3 показана часть разбиения внутреннего пространства между проводниками на элементарные ячейки – треугольники. Пусть вершины треугольников пронумерованы так, что первые N₁ вершин лежат на внешнем проводнике, вершины с номерами от N₁+1 до N₂ лежат на внутреннем проводнике, а всего разбиение содержит M вершин.

Задача определения потенциала  в каждой точке пространства может быть сведена к задаче минимизации следующего функционала :

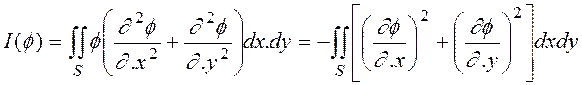(1),      где S – область, в которой ищется потенциал, то есть область, заключенная между внешним и внутренним проводниками (рис. 3).

Под минимизацией функционала понимается поиск такой функции , на которой интеграл в (1) достигает своего минимального значения. Из теории уравнения Лапласа известно, что функция, для которой функционал (1) достигает своего минимума, одновременно является решением уравнения Лапласа в той же области S.

Ключевым моментом метода конечных элементов является представление неизвестной функции (x,y) в виде разложения по известным базисным функциям с неизвестными коэффициентами в пределах каждой элементарной ячейки. Это разложение имеет следующий вид:

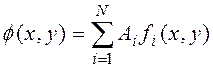,                                                             (2)

где - неизвестные коэффициенты,  - базисные функции. Коэффициенты  ищутся из условия минимума функционала (1), приме-ненного к каждому элементарному треугольнику разбиения. Совокупность этих условий, записанных для всех элементарных ячеек, позволяет записать искомую СЛАУ относительно неизвестных коэффициентов .

Особенностью МКЭ является то, что в качестве неизвестных коэф-фициентов  берутся значения неизвестной функции  в вершинах треугольников для самой простой аппроксимации потенциала (конкретный ее вид мы рассмотрим ниже). Если речь идет о более сложных функциях, аппроксимирующих потенциал в пределах элементарной ячейки, то в до-полнение к значениям  в вершинах добавляются значения потенциала в других характерных точках. Таким образом, в МКЭ используется сле-дующее представление неизвестной функции:

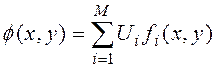,                                                              (3)

где  - значения потенциалов в характерных точках,  M – количество