Приведение квадратной матрицы к диагональному виду. Критерии приводимости квадратной матрицы к диагональному виду

§ 2. Приведение квадратной матрицы к диагональному виду

Говорят, что квадратная матрица А с элементами из поля P приводится к диагональному виду над P, если существует невырожденная квадратная матрица Т с элементами из P такая, что матрица  – диагональная.

Критерии приводимости квадратной матрицы к диагональному виду. 1. Если А – квадратная матрица -го порядка с элементами из поля P,  – линейное пространство над Р,  – тот линейный оператор, матрица которого в некотором базисе пространства  совпадает с А, то для приводимости матрицы А к диагональному виду над полем Р необходимо и достаточно, чтобы в  существовал базис, состоящий из собственных векторов оператора f.

2. Для того чтобы квадратная матрица А n-го порядка приводилась к диагональному виду над полем Р необходимо и достаточно, чтобы все корни  ее характеристического уравнения принадлежали этому полю и для каждого из них выполнялось условие

,                                                (7)

где  – кратность корня  характеристического уравнения матрицы А.

При решении задач первый критерий, пожалуй, проще в применении, хотя студенты обычно предпочитают второй.

В том случае, когда все характеристические числа матрицы А различны и принадлежат полю Р, эта матрица приводится к диагональному виду над Р. Если матрица А приводится к диагональному виду – матрице , то диагональными элементами последней являются собственные значения матрицы А, а матрица Т, приводящая А к диагональному виду, есть не что иное, как матрица перехода от исходного базиса к базису из собственных векторов.

Из всего вышесказанного вытекает, что для приведения квадратной матрицы к диагональному виду над полем Р следует:

1) составить характеристический многочлен матрицы А и найти его корни. Если какой-либо из них не принадлежит полю Р, то А к диагональному виду не приводится;

2) если все корни характеристического уравнения принадлежат полю Р, то для кратных корней проверить условие (7) (для однократных оно выполняется всегда). Если для какого-то из корней (7) не выполняется, то А к диагональному виду не приводится;

3) если для каждого из собственных значений условие (7) выполняется, то А к диагональному виду приводится. Записываем этот диагональный вид – матрицу , располагая на ее главной диагонали собственные значения  в произвольном порядке, причем каждое из значений повторяется столько раз, какова его кратность;

4) для каждого из найденных собственных значений находим собственные векторы и составляем из них базис;

5) записываем матрицу Т, приводящую А к диагональному виду, – матрицу перехода от исходного базиса к базису из собственных векторов, сохраняя порядок, установленный матрицей .

Пример 1. Найти диагональный вид матрицы А над полем действительных чисел и невырожденную матрицу Т, приводящую к этому диагональному виду, если

.

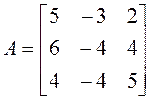►Проводим решение по намеченному плану.

                                      +

.

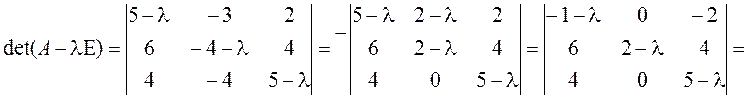2.Все корни действительны и однократны, поэтому матрица А приводится к диагональному виду.

3. .

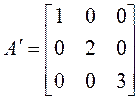4. Все собственные векторы можно найти с помощью алгебраических дополнений. Кроме того, вспомним, что, если мы нашли один собственный вектор, то любой вектор, ему коллинеарный, также является собственным с тем же самым собственным значением.

:   ;  , 

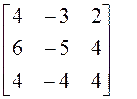(алгебраические дополнения к элементам первой строки);

:     ;     =

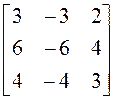(алгебраические дополнения к элементам второй строки);

:     ; ,

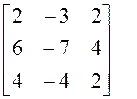(алгебраические дополнения к элементам первой строки).

5. Составляем матрицу  перехода от исходного базиса к, построенному базису , записывая в столбцы матрицы  координатные столбцы векторов ,  и  соответственно:

.◄

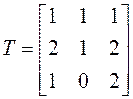Пример 2. Проверить, приводится ли матрица А к диагональному виду. Если приводится, найти этот диагональный вид и невырожденную матрицу Т, приводящую нему.

.

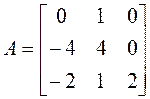►Составляем и решаем характеристическое уравнение:

.

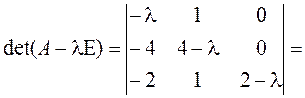
Матрица имеет только одно собственное значение , но его кратность равна трем. Проверяем выполнение условия (4.58):

.

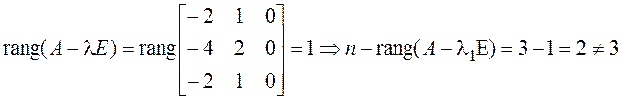Условие не выполняется, значит, матрица к диагональному виду не приводится.◄

Пример 3. Проверить, приводится ли матрица А к диагональному виду. Если приводится, найти этот диагональный вид и невырожденную матрицу Т, приводящую нему.

.

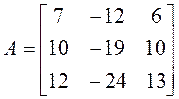► Решение опять проводим по намеченному плану.

1.

                                             –

.

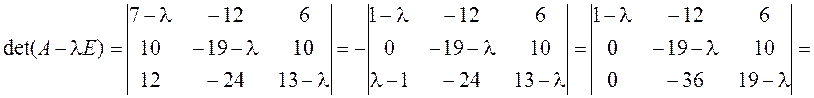2. Проверяем выполнение условия (7) для кратного корня:

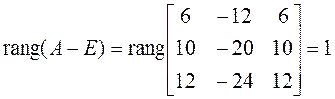.                                    (8)

Таким образом, , условие выполняется, матрица к диагональному виду приводится.

3. .

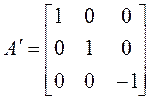4. Так как , то , т. е для первого собственного значения можно найти два линейно независимых собственных вектора. По одной из строк матрицы (8), разделив все ее элементы на общий множитель, выписываем единственное уравнение для отыскания координат собственных векторов и решаем его: , . В качестве двух линейно независимых решений можно взять, например