Свободные колебания. Бегущие и стоячие волны

I семестр         ЛЕКЦИЯ 9

2.5.6  Свободные колебания. Бегущие и стоячие волны.

Итак, получено частное решение уравнения свободных колебаний в виде

,

где

•  - собственная форма (нормированная тем или иным способом), соответствующая собственной частоте ω_к,
•  - функция времени,
• А_к и φ_к- постоянные интегрирования, определяемые из начальных условий,.которым должно удовлетворять общее решение.

Общее решение однородного дифференциального уравнения представляют собой сумму (суперпозицию) частных решений. На языке механики это звучит так: в общем случае свободные колебания представляют собой сумму собственных колебаний

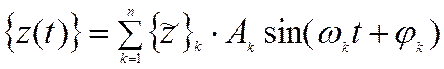
или

,

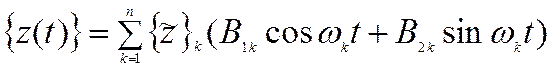где и  или и  - определяются начальными условиями.

Решение 

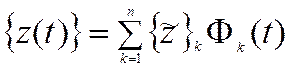
или в матричном виде

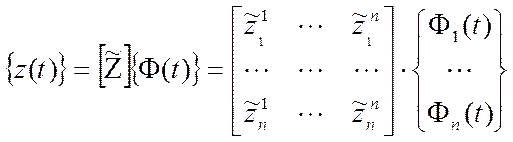
называется разложением по собственным формам.

Таким образом, частное решение представляет собой движение с сохранением формы (смещения масс пропорциональны одному параметру). Движение с сохранением формы называют стоячей волной. Для реализации такого движения необходимо специальным образом задать начальные условия, а именно начальное возмущение задать в виде собственной формы.

Сумма стоячих волн представляет собой бегущую волну:

2.5.7   Функции времени при учете сил сопротивления

Выше отмечалось, что учет сил диссипации, в общем случае, значительно усложняет решение системы уравнений движения, делая невозможным, в общем случае, разложение решения по собственным формам. Были перечислены случаи, в которых учет диссипации не обременителен. К таким случаям относится так называемое внешнее демпфирование, когда матрица диссипативных коэффициентов пропорциональна матрице жесткости.

Уравнения свободных колебаний при наличии диссипации:

 или .

В случае внешнего демпфирования принимают вид

 и ,

 который можно преобразовать

 и .

Для полученных уравнений функция времени в решении разложением по собственным формам имеет вид:

,

где  .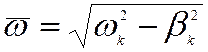

2.6   Вынужденные колебания систе м с конечным числом степеней свободы

2.6.1      Вводные замечания

Решение системы дифференциальных уравнений – вектор, матрица-столбец – есть сумма общего решения однородного уравнения и частного решения:

начальные условия

1.   Гармоническое возбуждение колебаний 2.    Произвольная нагрузка         решение численными методами         разложение решения по собственным          формам.

2.6.2   Вибрационная нагрузка (гармоническое возмущение) при отсутствии вязкого сопротивления.

I.    Система уравнений и ее решение.

,

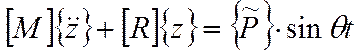где  - столбец амплитудных значений нагрузки;

θ- частота возмущения.

Частное решение неоднородного дифференциального уравнения  ищут в виде: ,

где - матрица - столбец амплитудных значений перемещений по направлениям степеней свободы.

Тогда     .

Подстановка решения в уравнение в прямой форме приводит уравнение к виду

.

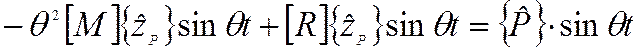Так как t-произвольный момент времени, этой записи эквивалентно алгебраическое матричное неоднородное уравнение

.

Если матрица - имеет обратную, то

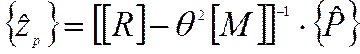
Матрица  может быть названа матрицей жесткости при гармонической нагрузке.  Обозначим ее  . Тогда

.

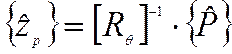Таким образом, эпюра перемещений зависит

• от эпюры нагрузки
• от частоты возмущающей силы,

но не зависит от времени – установившиеся вынужденные колебания.

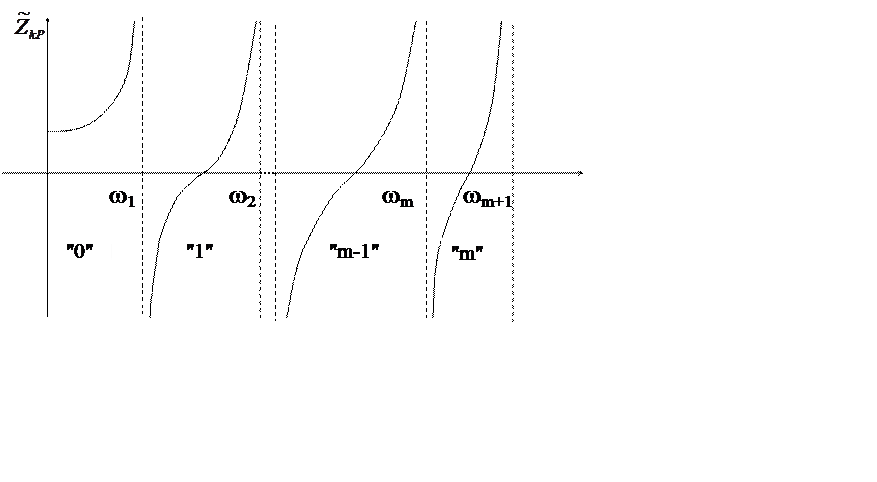
II.     Амплитудно-частотная характеристика – график зависимости амплитудного значения характерного перемещения от частоты возмущения.

1.  Меняем значение θ,

2.  Вычисляем матрицу

3.  Вычисляем обратную ей матрицу

4.  Умножаем обратную матрицу на столбец амплитудных значений приложенных сил

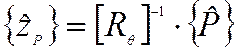
5.  Получаем матрицу-столбец (вектор) амплитудных значений перемещений

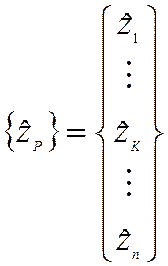
6.  Значение перемещения, выбранного в качестве характерного, определит точку графика.

Заметим, что

• при совпадении частоты возмущения с любой из спектра собственных частот матрица становится вырожденной, т.к. ее определитель равен нулю, и, значит, не имеет обратной. В этих местах график имеет разрывы при   и пики при  .
• вид графика зависит от выбора характерной точки в сочетании с эпюрой нагрузки.