4П. Приложение: Двойственные задачи
1. Двойственные задачи линейного программирования
2. Связь между решениями исходной и двойственной задач
3. Симплексный метод
4. Метод одновременного решения пары двойственных задач
1. Двойственные задачи линейного программирования
Каждой задаче линейного программирования можно поставить в соответствие задачу, называемую двойственной к исходной.
Предположим, что в производстве используется m различных видов ресурсов, объем которых ограничен величинами b1, b2,.., bm. И производится n различных видов продукции, величина выпуска которых определяется переменными х1, х2,…, хn. Известны нормы затрат каждого ресурса на единицу каждого вида продукции – в виде матрицы
![]()
![]() а11 а12
...
а1n
а21
а22 ...
а2n
...
... ... ... m1 m2 ...
аmn.
а11 а12
...
а1n
а21
а22 ...
а2n
...
... ... ... m1 m2 ...
аmn.
а
Известна также стоимостная оценка (цена) единицы продукции каждого вида с1, с2,…, сn.
Задача сводится к следующему: найти такие значения переменных х1, х2,…, хn, при которых расход ресурсов не превышает заданного их количества, а стоимость всей продукции достигает максимума. Математически задача записывается следующим образом: максимизировать
L = c1x1+c2x2+…+cnxn (1)
а11х1 а12х2 ... а1пхп b1
а21х1 а22х2 ... а2пхп b2 .....................................
 при условиях ат1х1 ат2х2 ...
атпхп bт
(2) х j 0 (j=1, 2,.., n).
при условиях ат1х1 ат2х2 ...
атпхп bт
(2) х j 0 (j=1, 2,.., n).
На базе тех же исходных данных можно поставить еще одну задачу, в которой переменные величины суть оценки у1,у2,…,уm, приписываемые каждому виду ресурсов. Они должны быть такими, чтобы общая оценка всего наличного количества ресурсов была минимальной, но при условии, что суммарная оценка ресурсов, расходуемых на единицу любого вида продукции, будет не меньше, чем цена за эту единицу.
Математически задача записывается следующим образом: минимизировать
L = b1y1+b2y2+…+bmym (3)
а11у1 а21у2 ... ат1ут с1
а12у1 а22у2 ... ат2ут с2
...........................................
а1п у1 а2п у2 ... атп ут сп
 при
условиях уi 0
(i 1,2,...,m) (4)
при
условиях уi 0
(i 1,2,...,m) (4)
Задачи (1) – (2) и (3) – (4) образуют пару взаимодвойственных задач, и любая из них может рассматриваться как исходная.
Сосредотачивая внимание на экономическом содержании и размерности постоянных и переменных величин рассматриваемых задач, можно записать соотношения. Для прямой (исходной) задачи: максимизируемая функция
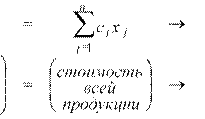
![]() с
j x
jmax
с
j x
jmax
стоимостьразмеры
единицывыпускаmax
продукциипродукции
ограничивающие условия
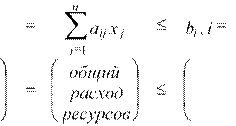
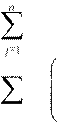
![]()
![]() аij x
j1,2,...,m
аij x
j1,2,...,m
нормы расходаразмеры объем ресурсов навыпуска имеющихся единицу продукциипродукции ресурсов
.
Для двойственной задачи: минимизируемая функция

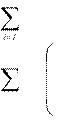
![]() т
т
bi yimin
объемоценки
имеющихсяединицыmin
ресурсовресурсов
ограничивающие условия
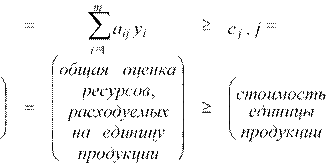
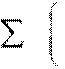
![]()
![]()
![]() аij уi 1,2,...,n
аij уi 1,2,...,n
нормы расходаоценки на единицуединицы продукцииресурсов
.
Эти задачи обладают следующими свойствами:
1. В одной задаче ищется максимум целевой функции, в другой – минимум.
2. Коэффициенты при переменных в целевой функции одной задачи суть свободные члены системы ограничений другой задачи, и наоборот.
3.
![]() В
каждой задаче система ограничений задается в виде неравенств, причем в задаче,
где ищется максимум целевой функции, все неравенства вида « », а в задаче, где
находится минимум целевой функции, все неравенства вида « ».
В
каждой задаче система ограничений задается в виде неравенств, причем в задаче,
где ищется максимум целевой функции, все неравенства вида « », а в задаче, где
находится минимум целевой функции, все неравенства вида « ».
4. Коэффициенты при переменных системах ограничений записываются матрицами
![]()
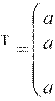
![]()
![]() а11 а12 ... а1n11
а21
...
ат1 а21 а22 ... а2nА12
а22 ...
ат2
а11 а12 ... а1n11
а21
...
ат1 а21 а22 ... а2nА12
а22 ...
ат2
А
... ... ... ...... ... ... ...
m1 аm2 ... аmn 1п а2п ... аmn, транспонированными относительно друг друга.
5. Число неравенств в системе ограничений одной задачи совпадает с числом переменных в другой задаче.
6. Условия неотрицательности переменных сохраняются в обеих задачах.
Пример. Исходная задача L = 10x1+6x2-4x3 min
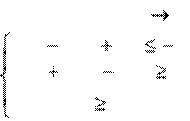 2х1 2х2 5х3 3
2х1 2х2 5х3 3х1,х2 ,х3 0
Приводим все неравенства системы ограничений исходной задачи к одному знаку: L = 10x1+6x2-4x3 min
3х1 9х2 х3 2
2х1 2х2 5х3 3
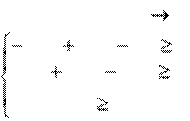 х1,х2 ,х3 0
х1,х2 ,х3 0
Двойственная задача L = 2y1+3y2 max
3у1 2у2 10
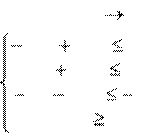 9у1
2у2 6 у1 5у2 4
9у1
2у2 6 у1 5у2 4
2. Связь между решениями исходной и двойственной задач
Теорема двойственности
Если одна из пары двойственных задач имеет оптимальный план, то другая тоже имеет оптимальный план, и значения целевых функций задач равны между собой, то есть Lmax =
![]() Lmin.
Если же целевая функция одной из пары двойственных задач не ограничена, то
другая задача вообще не имеет решения.
Lmin.
Если же целевая функция одной из пары двойственных задач не ограничена, то
другая задача вообще не имеет решения.
Нахождение решения двойственных задач
Графический метод решения
Если число переменных в исходной и двойственной задачах, образующих пару задач, равно двум, то, используя геометрическую интерпретацию ЗЛП, можно легко найти решение этой пары задач. При этом имеют место три случая:
1) обе задачи имеют решение; 2) решение имеет одна задача; 3) обе задачи не имеют решения.
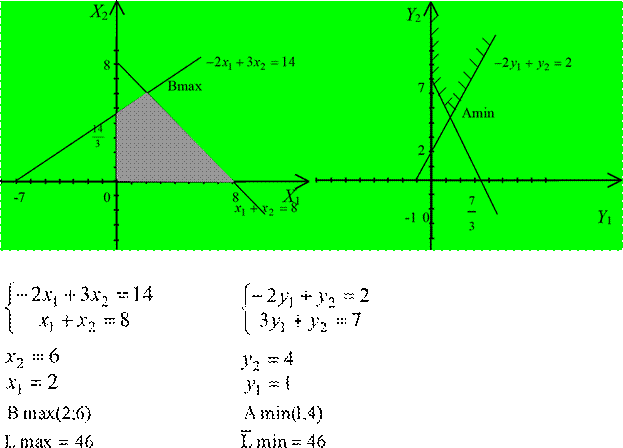
Пример 1.
Исходная задача Двойственная задача L = 2х1+7х2 max L = 14у1+8у2 min

 2х1 3х2 14
2у1 у2 2
х1 х2 8
3у1 у2 7
2х1 3х2 14
2у1 у2 2
х1 х2 8
3у1 у2 7
х1,х2 0 у1, у2 0
 |
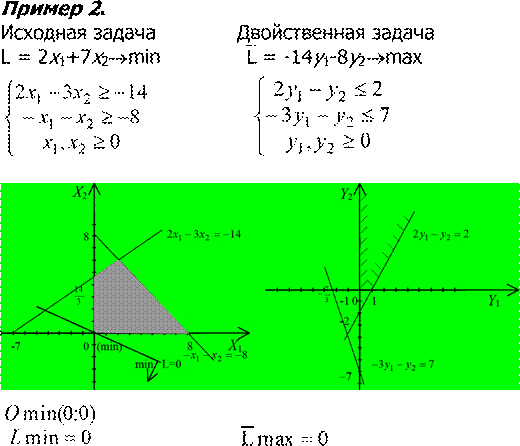 |
Пример 3.
Исходная задача Двойственная задача
![]()
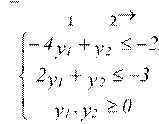
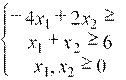 L
= -2х1-3х2 min L
= 4у+6у max
L
= -2х1-3х2 min L
= 4у+6у max
4
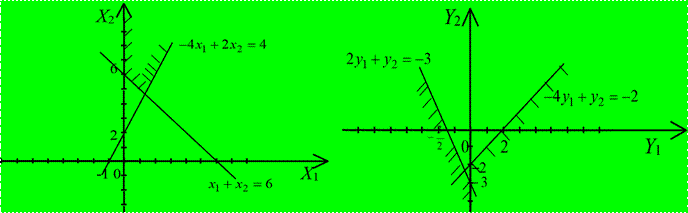
Исходная задача не имеет оптимального решения из-за неограниченности снизу ее целевой функции на множестве допустимых решений, тогда двойственная к ней задача вообще не имеет решения.
3. Симплексный метод
Исходная задача Двойственная задача
![]() L = х1+2х2+3х3 min L
= 4у1+6у2 max
L = х1+2х2+3х3 min L
= 4у1+6у2 max
2у1 5у2 1
2х1 3х2 х3 4 3у1 у2 2
 5х1
х2 2х3 6 у1 2у2 3
5х1
х2 2х3 6 у1 2у2 3
х1,х2,х3 0 у1, у2 0
Решим обе задачи табличным симплексным методом L – х1-2х2-3х3=0 L – 4у1-6у2 = 0
2у1 5у2 у3 1
 2х1 3х2 х3 х4 4 3у1 у2 у4 2
2х1 3х2 х3 х4 4 3у1 у2 у4 2
5х1 х2 2х3 х5 6 у1 2у2 у5 3
![]()
![]() х1,х2,х3,х4,х5 0
у1,
у2,
у3,
у4,
у5 0
х1,х2,х3,х4,х5 0
у1,
у2,
у3,
у4,
у5 0
|
|
|
|
|
|
х1 |
х2 |
х3 |
х4 |
х5 |
св. |
|
х5 |
0 |
|
|
|
1 |
4 |
|
х1 |
1 |
3
|
|
|
0 |
2 |
|
L |
0 |
|
|
|
0 |
2 |
Lmax=2
1 1 7
![]() Ymax(
2;0;0;
2;
2)
Ymax(
2;0;0;
2;
2)
Lmin=2
Xmin(2;0;0;0;4)
Как видно из примеров, каждая из задач двойственной пары есть самостоятельная ЗЛП и может решаться независимо от другой. Но при нахождении оптимального решения одной задачи можно найти
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.