Уравнения математической физики. Волновое уравнение для прямоугольника. Вторая краевая задача для однородного уравнения теплопроводности, страница 2

41. Метод продолжений используется для решения задачи Коши. Может ли этот  метод быть использован при решении краевых задач для волнового уравнения? 

Ответ: Да (1)

42. Метод Фурье применим:

Ответ: не только к уравнениям с постоянными коэффициентами: они могут быть заданными непрерывными функциями от  и ()

43. Найти общее решение дифференциального уравнения :

Ответ: (или ) ()

44. Найти решение уравнения , если :

Ответ: ()

45. Найти решение уравнения , если :

Ответ:  (4)

46. Написать ограниченное в круге решение уравнения :

Ответ:   (2)

47. Общее решение уравнения 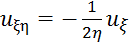 имеет вид:  

Ответ:  ()

48. Однородно или неоднородно условие периодичности ?

Ответ:  Да ()

49. Поставить задачу о нестационарном распространении тепла в конечном стержне, концы которого теплоизолированы, а начальное распределение температуры удовлетворяют условию : 

Ответ:  (2)

50. Поставить краевую задачу о малых поперечных колебаниях струны в среде с сопротивлением,   пропорциональным    скорости,   предполагая,  что   концы струны закреплены жестко:

Ответ:  ()

51. Поставить краевую задачу о малых поперечных колебаниях струны, предполагая, что левый конец струны закреплен, а правый свободен:

Ответ:   ()

52. Применим ли метод Фурье для решения однородного уравнения в случае, когда искомая функция зависит не от двух, а от большего числа переменных?

Ответ:  Да (1)

53. Решение внешней задачи Дирихле для круга имеет вид:

Ответ: 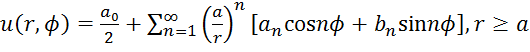(4)

54. Решение 1-й краевой задачи для однородного волнового уравнения с однородными условиями имеет вид:

Ответ: (3)

55. Решение волнового одномерного уравнения методом Фурье сводится:

Ответ: к интегрированию двух обыкновенных дифференциальных уравнений ()

56. Решение задачи Дирихле в одномерном случае, если : 

Ответ:  ()

57. Решение задачи Дирихле для круга можно получить методом:

Ответ:  разделения переменных, функций Грина, потенциалов (4)

58. Решение задачи Дирихле на плоскости для области, ограниченной контуром  сводится к решению интегрального уравнения 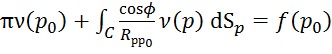 из которого определяется:

Ответ: функция  (2)

59. Решение задачи Коши для неоднородного волнового уравнения выражается формулой:

Ответ: Эйлера  (или Даламбера) ()

60. Решение краевой задачи должно удовлетворять:

Ответ:  уравнению, граничным и начальным условиям ()

61. Решение уравнения  для внешнего круга имеет вид:

Ответ: (3)

62. Уравнение  при  имеет решение:

Ответ: (3)

63. Уравнение  имеет решение вида:

Ответ:  ()

64. Уравнение есть:

Ответ: Уравнение гиперболического типа ()

65. Уравнение есть уравнение типа:

Ответ: гиперболического ()

66. Уравнение  есть уравнение:

Ответ:  трехмерное неоднородное волновое (3)

67. Уравнение :

Ответ:  эллиптическое (3)

68. Уравнение  имеет решения: 

Ответ:  (3)

69. Уравнение  описывает:

Ответ: Установившееся течение жидкости. Стационарные тепловые поля.()

70. Уравнение  есть:

Ответ: Волновое уравнение (распространение электромагнитных волн в вакууме, распространение звуковых волн)()

71. Уравнение 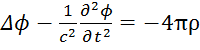 есть: 

Ответ:  волновое (1)

72. Уравнение  есть: 

Ответ:   уравнение Гельмгольца(4)

73. Уравнение есть уравнение:

Ответ: свободных колебаний.(3)

74. Уравнение есть уравнение:

Ответ:  гиперболического типа(?)

75. Уравнение есть уравнение характеристик для уравнения:

Ответ:  эллиптического типа(3)

76. Уравнение Гельмгольца в произвольной системе координат имеет вид:

Ответ:  (4)

77. Уравнение Гельмгольца в цилиндрической системе координат имеет вид:

Ответ:    (3)

78. Уравнение Гельмгольца получается из уравнения:

Ответ:  (3)

79. Уравнение Пуассона   в круге радиуса  с граничным условием  решается:

Ответ:  полагается , где  - частное решение уравнения Пуассона, а  - решение уравненияЛапласа  (2)

80. Уравнение Пуассона имеет вид: 

Ответ:   (3)

81. Уравнение Пуассона сводится к уравнению Лапласа заменой:

Ответ:  , где  - частное решение уравнения Пуассона ()

82. Уравнение теплопроводности при решении задачи в круге в случае осевой симметрии имеет вид: 

Ответ:  (?)

83. Формула есть формула:

Ответ:    Грина (2)

84. Характеристическое уравнение имеет вид:  

Ответ:    (3)

85. Что сначала нужно сделать для решения задачи  при условиях :

Ответ: Обнулить граничные условия и разбить задачу на две (3)