B) краевая задача, задача на собственные значения.
C) задача Коши, краевая задача.
3.2. Расчетная формула метода Эйлера решения задачи Коши имеет вид:
A) yn+1 = yn + hnf(xn,yn).
B) yn+1 = yn + h2nf(xn,yn).
C)
![]() .
.
3.3. Погрешность формулы Эйлера для каждогоучасткаинтегрирования [xn,xn+1] имеетпорядок:
A) O(h2n). B) O(hn). C) O(h3n).
3.4. При выводе расчетной формулы метода
Эйлера учитываются первые
A)два члена разложения Тейлора. B)три члена разложения Тейлора.
C)четыре члена разложения Тейлора.
3.5. При выводе расчетной формулы метода Рунге-Куттавторогопорядкаточностиучитываются первые
A)два члена разложения Тейлора. B)три члена разложения Тейлора.
C)четыре члена разложения Тейлора.
3.6. При выводе расчетной формулы метода Рунге-Кутта четвертого порядка точности учитываются первые
A)пять членов разложения Тейлора.
B)три члена разложения Тейлора.
C)четыре члена разложения Тейлора.
3.7. Схема Рунге-Кутта второго порядка точности имеет вид:
A)
![]() .
.
B)
![]() .
.
C)
![]() .
.
3.8. Схема Рунге-Кутта четвертого порядка точности имеет вид:
A)
![]() ,
,
где
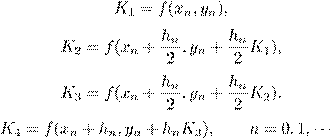 .
.
B)
![]() ,
,
где
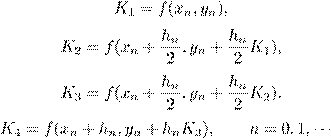 .
.
C)
![]() ,
,
где
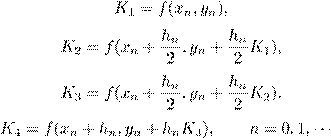 .
.
3.9. Погрешность схемы Рунге-Кутта че твертого порядка точности на каждом отрезке
[xn,xn+1] есть величина порядка
A)O(h5n). B)O(h4n).
C)O(h3n).
3.10. Схемы Рунге-Кутта для одного дифференциального уравнения
A) обобщаются на случай систем уравнений.
B) необобщаютсянаслучайсистемуравнений.
C) иногда можно обобщить на случай систем уравнений.
4.1. При использовании метода сеток при решении дифференциальных уравнений с частными производными приходим к системе линейных алгебраическихуравнений, вкоторойчислонеизвестных
A) равно числу внутренних узлов сетки.
B) равно числу граничных узлов сетки.
C) равно числу всех узлов сетки.
4.2. В методе сеток заданное дифференциальное уравнение заменяется соответствующим конечно-разностным уравнением
A) во всех внутренних узлах построенной сетки.
B) вовсехграничныхузлахпостроеннойсетки.
C) во всех узлах построенной сетки.
4.3. Для каждого внутреннего узла квадратной сетки уравнение Пуассона заменяется разностным уравнением
![]()
с погрешностью
A) O(h2).
B) O(h).
C) O(h3).
4.4. Для каждого внутреннего узла квадратной сетки уравнение Пуассона заменяется разностным уравнением
![]() .
.
При этом в разностной схеме участвуют
A) пять узлов.
B) шесть узлов.
C) четыре узла.
4.5. Прирешениизадачметодомсетоквозникаетпогрешность, котораясостоитизпогрешности методаивычислительнойпогрешности. Погрешность метода включает:
A) погрешность, возникающую в результате замены дифференциального уравнения разностным.
B) погрешность аппроксимации граничных условий.
C) погрешность, возникающую в результате замены дифференциального уравнения разностным и погрешность аппроксимации граничных условий.
4.6. Уравнение теплопроводности аппроксимируетсяразностнымуравнениемнапрямоугольной сетке
![]()
A) с погрешностью O(l + h2).
B) с погрешностью O(l2 + h2).
C) с погрешностью O(l2 + h).
4.7. Уравнение теплопроводности аппроксимируетсяразностнымуравнениемнапрямоугольной сетке
![]()
A) с погрешностью O(l + h2).
B) с погрешностью O(l2 + h2).
C) с погрешностью O(l2 + h).
4.8. Неявные схемы
A) всегда устойчивы.
B) всегда неустойчивы.
С) иногда устойчивы.
4.9. Метод прогонки решения разностной краевой задачи для уравнения теплопроводности A) устойчив для любой сетки.
B) неустойчив для любой сетки.
C) устойчив не для всякой сетки.
4.10. Волновое уравнение аппроксимируется разностным уравнением на прямоугольной сетке
![]()
A)с погрешностью O(h2 + l2).
B)с погрешностью O(h + l2). C)с погрешностью O(h2 + l).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.