Уравнения геометрических объектов на плоскости. Виды уравнений прямой на плоскости. Уравнение прямой проходящей через две точки

АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ

Аналитическая геометрия изучает геометрические объекты и связи между ними используя их  аналитические представления в виде уравнений.

УРАВНЕНИЯ  ГЕОМЕТРИЧЕСКИХ  ОБЪЕКТОВ НА ПЛОСКОСТИ

Геометрические объекты в аналитической геометрии определяются как геометрическое место точек, координаты которых в некоторой системе координат, удовлетворяют одному или системе уравнений, т.е. геометрическая задача сводится к алгебраической. Простейшими геометрическими объектами являются линейные объекты, которые задаются одним или системой линейных уравнений ( т.е. содержащие координаты точек в первой степени).

Рассмотрим сначала линейные объекты на плоскости, к которым относятся прямая и точка как пересечение двух прямых

Виды уравнений прямой на плоскости:

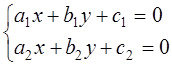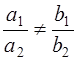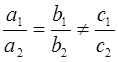Общее уравнение прямой. A x+B у+C = 0 – общее уравнения прямой на плоскости. Система двух линейных уравнений  с геометрической точки зрения представляет уравнения двух прямых на плоскости. При этом можно рассматривать три случая:1)прямые пересекаются и решение системы определяет единственную точку пересечения (линейный объект); 2) прямые параллельны и система не имеет решения; 3)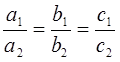прямые совпадают, система имеет бесчисленное множество решений

Теорема: Пусть дано общее уравнение прямой Ах+By+C=0 (1), где A, B одновременноне равны нулю, то плоский вектор n=(A,B) ортоганален прямой заданной уравнением (1) и поэтому называется нормальным вектором прямой.

Доказательство: подставим координаты точки М₀ лежащей в плоскости в уравнение (1) и получим Ах₀+By₀+C=0 (1¢). Вычтем (1)–(1¢) получим А(х–х₀)+B(y–y₀)=0. Если вектор М₀М=(х–х₀, y–y₀), то  слева в полученном равенстве записано скалярное произведение векторов, оно равно 0, значит n и M₀M ортоганальны, следовательно вектор n ортогонален прямой. Вектор n=(A,B) называется нормальным вектором прямой.

Замечание: Пусть уравнения А₁х+B₁y+C₁=0 и А₂х+B₂y+C₂=0 определяют одну и ту же прямую, тогда найдется такое действительное число t, что А₁=t^.А₂ и В₁=t^.В₂ ,т.о нормальный вектор определяется не однозначно , он лишь задает перпендикулярное прямой направление.

Кроме общее уравнение прямой часто используются при решении задач другие виды уравнений прямой

2) у= kx+ b -уравнение с угловым коэффициентом  k  и cмещением b; Угловым коэффициентом прямой, не параллельной оси ОУ называется число k, равное tga угла, на который нужно повернуть против часовой стрелки положительную часть оси ОХ, чтобы она стала параллельной данной прямой. С помощью углового коэффициента k можно легко определить угол между прямыми j= j₂–j₁ tgj =(k₂ -k₂)/(1+k₁k₂). Для перпендикулярных прямых: 1+k₁k₂=0 Для параллельных прямых: k₁=k₂.

3) 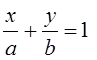-уравнение прямой в отрезках, где (а, b )- отрезки, отсекаемые на осях координат (c учетом знака). Геом.смысл: прямая отсекает на осях координат отрезки а и b

4) Каноническое уравнение прямой 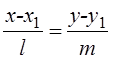 Пусть на прямой задана точка M₁(х₁;y₁)и направляющий. вектор прямой (параллельный прямой) а(l, m). Возьмем на прямой произвольную точку. М и вектор лежащий на прямой M₁М=(х–х₁; y–y₁), который параллелен направляющему вектору а(l, m) и  поэтому координаты векторов пропорциональны.

5) Уравнение прямой проходящей через две  точки А(х₁, у₁) и В(х₂, у₂). 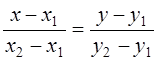 Пусть на прямой заданы две точки М₁(x₁;y₁) и М₂(x₂;y₂). Т.к. на прямой заданы две точки, то задан направляющий вектор а (x₂–x₁; y₂–y₁)

6). Нормальное уравнениее прямой. xcosa+ysina–р=0 (ОР – перпендикулярный вектор из начала координат к прямой |ОР|= р>0 – расстояние от прямой до начала координат,a – угол между вектором ОР и положительным напр. оси ОХ.

Параметрическое уравнение прямой.

Прямая на плоскости частный случай прямой в пространстве.

У прямой в пространстве нет понятия нормального вектора.

Определение: если хотя бы один из коэффициентов в уравнении (1) =0, то уравнение называется неполным.

1. С=0,                   Ах+By=0 – проходит через (0,0)

2. С=0, А=0, By=0, значит у=0

3. С=0, B=0, Ах=0, значит х=0

4. А=0,         By+C=0, паралл. ОХ

5. B=0,                   Ах+C=0, паралл. OY

j,   – угол наклона прямой. tg угла наклона называется угловым коэффициентом прямой k=tg j, 

Пусть прямая задана в каноническом виде. Найдем угловой коэффициент прямой tg j,   = m/l. Тогда видим x–x₁/l/l=y–y₁/m/l. y–y₁=k(x–x₁) при y₁–kx₁=b, y=kx+b

Задача: записать уравнение прямой , если изветны р и a

Решение: Выделим на прямой ОР вектор ед. длины n. (|n|=1, n=(cosa, sina)). Пусть М(x,y) – произв.точка прямой. Рассмотрим два вектора n и ОМ. Найдем двумя способвами их скал.произведение. 1. ОМ^.n=|OM|^.|n|cosÐMOP=р. 2. ОМ^.n=cosax+sinay. Приравняем правые части.

Задача: прямая задана общим ур–ем Ах+By+C=0. Перейти к норм. виду. xcosa+ysina–p=0

т.к. уравнения определяют одну прямую, то сущ. коэфф. пропорциональности.

Cos²a=(A^.t)²

Sin²a=(B^.t)²

-p=C^.t

cos²a+sin²a=t²(A²+B²),     t²=1/A²+B²,   t=±(1/ A²+B²). Sign t= – sign C

Что бы найти нормальное уравнение прямой нужно общее ур–е умножить на t.

Аtх+Bty+Ct=0, t–нормирующий множитель.

7. Система: x=lt+x₁ и y=mt+y₁

НОРМАЛЬНОЕ УРАВНЕНИЕ ПРЯМОЙ. Расстояние от точки до прямой.

1. xcosa+ysina–p=0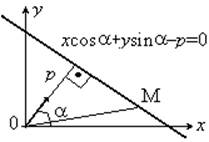

a – угол между вектором ОР и положительным напр. оси ОХ.

Задача: записать ур–е прямой , если изветны р и a

Решение: Выделим на прямой ОР вектор ед. длины n. |n|=1, n=(cosa, sina). Пусть М(x,y) – произв.точка прямой. Рассмотрим два вектора `n и `ОМ. Найдем двумя способвами их скал.произведение.

1.  ОМ×`n=|OM||n|cosMOP=р.

2.  . ОМ×`n=хcosa+уsina. Приравняем правые части.

Задача: прямая задана общим ур–ем. Перейти к норм. виду.

Ах+By+C=0

xcosa+ysina–P=0

т.к. уравнения определяют одну прямую, то сущ. коэфф. пропорциональности.

Cos²a=(A×t)²

Sin²a=(B^.t)²

–p=C^×t

cos²a+sin²a=t²(A²+B²),     t²=1/A²+B²,   t=±sqrt(1/ A²+B²). Sign t= – sign C

Что бы найти нормальное уравнение прямой нужно общее ур–е умножить на t.

Аtх+Bty+Ct=0, t–нормирующий множитель.

2. Обозначим d – расстояние от точки до прямой, а ч/з б – отклонение точки от прямой. б=d, если нач.коорд. и точка по разные стороны; = – d, если нач.коорд. и точка по одну сторону.

Теорема: Пусть задано нормальное уравнение прямой xcosa+ysina–P=0 и М₁(x₁;y₁), тогда отклонение точки М₁ = x₁cosa+y₁sina–P=0

Задача: найти расстояние от точки М₀(x₀;y₀) до прямой Ах+By+C=0. Т.к. d=|d|, то формула расстояний принимает