Вычислительные алгоритмы в системе аналитических вычислений Maple. Графики частичных сумм ряда при разных длинах мантиссы

УДК 624.04:519.6

Вычислительные алгоритмы в системе аналитических вычислений Maple

Санкт-Петербургский государственный университет

Системы аналитических вычислений (Maple, Mathematica и др.), являясь мощными инструментами аналитических вычислений, позволяют в тоже время реализовывать алгоритмы вычислительной математики с помощью встроенных в них языков программирования. Казалось бы зачем использовать эти системы для подобных целей, если существует целый ряд компилируемых языков программирования, предназначенных для реализации численных расчетов (Fortran, C, C++), тем более что языки программирования аналитических систем являются интерпретируемыми? Можно привести, по крайней мере, две причины использования систем аналитических вычислений для реализации вычислительных алгоритмов.

Первая связана с образовательными аспектами. Простота и легкость манипулирования длиной мантиссы в представлении вещественных чисел позволяет показать студентам природу вычислительной неустойчивости разнообразных алгоритмов, а наличие встроенных графических процедур способствует простой и нетрудоемкой визуализации пошагового выполнения вычислительных алгоритмов.

Вторую можно связать с научной сферой. Системы аналитических вычислений явились толчком к возрождению интереса к численно-аналитическим методам решения краевых задач теории упругости и строительной механики, расширяющих классы решаемых задач в виде рядов по тригонометрическим, степенным и специальным функциям.

В данной работе на примере вычисления синуса через его представление в виде степенного ряда показано использование системы Maple для знакомства обучаемых с проблемой вычислительной неустойчивости алгоритма, а на примере модифицированного алгоритма метода начальных параметров показано использование этой же системы для разработки практического алгоритма метода начальных параметров для решения краевых задач упругой балки на упругом Винклеровском основании.

Вычисление функции синуса степенным рядом

Вычислим функцию  с помощью ее степенного ряда

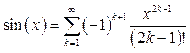,                                  (1)

теоретически сходящегося на всем множестве вещественных чисел . Для вычисления этого ряда с заданной абсолютной точностью  воспользуемся оценкой его остаточного члена

.                                                (2)

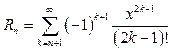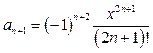Здесь  — остаточный член частичной суммы , а  — -й член ряда (1). Вычисления завершаем, когда . В таблице приведены результаты вычисления значения  при разных длинах мантиссы (системная переменная  Digits в Maple [1]) с абсолютной точностью .

Таблица. Вычисление

При длине мантиссы 8 (обычная точность) и 16 (удвоенная точность) результаты совершенно далеки от истинного значения. С увеличением длины мантиссы вычисленные значения приближаются к истинному, и только при длине мантиссы 25 результат попадает в заявленную точность. Заметим, что с теоретической точки зрения все результаты должны быть верными, так как абсолютная величина остаточного члена  меньше  в соответствии с (2). Недостоверность полученных результатов связана с накоплением ошибки при вычислении ряда (1): абсолютные значения его частичных сумм сначала возрастают, а потом убывают до величины, по модулю меньшей единицы. При больших значениях аргумента функции синуса максимальное значение частичной суммы может быть очень большим, а это и приводит к накоплению ошибки из-за недостаточной длины мантиссы. На рис. 1 показаны в полулогарифмической шкале графики частичных сумм  при расчетах с разными длинами мантиссы.

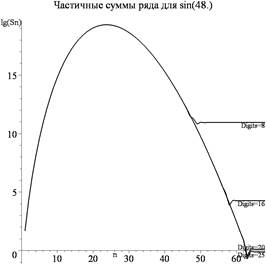
Рис. 1. Графики частичных сумм ряда (1) при разных длинах мантиссы

Максимальное значение частичной суммы ряда достигается при  и имеет порядок . Поэтому погрешность при вычислениях с длиной мантиссы Digits может достигать порядка , что и можно увидеть из графиков на рис. 1. Когда длина мантиссы равна 8, погрешность имеет порядок , при 16 она уменьшается до .

На практике функция синуса для больших значений аргументов, конечно, не вычисляется с использованием ряда (1), но этот пример дает возможность показать студентам природу возникновения вычислительной неустойчивости алгоритмов.

Алгоритм метода начальных параметров

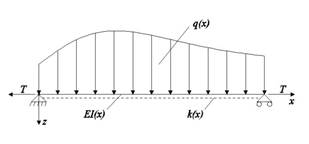
Рассмотрим тонкую балку длины  с относительно небольшой шириной  и с переменной вдоль ее оси жесткостью на изгиб, лежащую на упругом основании Винклера с переменным коэффициентом постели  и загруженную распределенной по всей длине нормальной к оси балки непрерывной нагрузкой  (рис. 2). Предполагается свободное без трения проскальзывание балки по плоскости контакта с основанием.

Обыкновенное дифференциальное уравнение четвертого порядка изгиба балки на упругом основании может быть  записано в матричной форме в виде системы четырех обыкновенных дифференциальных уравнений первого порядка

.                                       (3)

Здесь

,

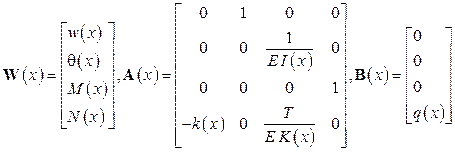 — прогиб балки по оси ,  — модуль упругости материала балки,  — момент инерции поперечного сечения балки относительно оси, проходящей через центр тяжести сечения, ,  — угол поворота сечения ,  и  соответственно момент и перерезывающая сила в сечении .