Validation for the Cox Model. Terry M. Therneau Mayo Foundation. Breslow estimates. Exact partial likelihood, страница 4

The robust variance for a Cox model is defined as D⁰D where the n × p dfbeta matrix D is based on the score residuals. Each row of D represents the infinitesimal jackknife, the derivative of β^ˆ with respect to a change in the case weight for subject i. It is fairly each to check this using a direct derivative,  where f is the vector of coefficients from a fit of the Cox model with the chosen weight for subject i (w_i will be 1 for most data sets). This shows that the Efron/Breslow chimera is less accurate than the S code. However, I have not seen any example where the effect on either D or the robust variance D⁰D was large enough to have practical consequences. Still, the numerical analyst in me prefers to avoid an inferior approximation.

1.3  Exact partial likelihood

At the tied death time the exact partial likelihood will have a single term. The numerator is a product of the risk scores of the subjects with an event, and the denominator is a sum of such products, where the sum is over all possible choices of two subjects from the four who were at risk at the time. (If there were 10 tied deaths from a pool of 60 available, the sum would be over all  subsets, a truly formidable computation!) In our case, three of the four subjects at risk at time 6 have a risk score of exp(0x) = 1 and one a risk score of r, and the sum has six terms {r,r,r,1,1,1}.

.

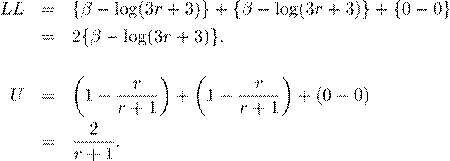
The solution U(β) = 0 corresponds to r = ∞, with a loglikelihood that asymptotes to −2log(3). The Newton–Raphson iteration has increments of (r+1)/r, so β^ˆ = 0, 2, 3.1, 4.2, 5.2, and so on. A solution at β^ˆ = 15 is hardly different in likelihood from the true maximum, however, and most programs will stop iterating shortly after reaching this point. The information matrix, which measures the curvature of the likelihood function, rapidly goes to zero as β grows.

Both SAS and S use the Nelson–Aalen estimate of hazard after fitting an exact model, so the formulae of Table 1 apply. All residuals at β^ˆ = 0 are thus identical to those for a Breslow approximation. At β^ˆ = ∞ the martingale residuals are still well defined. Subjects 1 to 3, those with a covariate of 1, experience a hazard of r/(3r + 3) = 1/3 at time 1. Subject 3 accumulates a hazard of 1/3 at time 1 and a further hazard of 2 at time 6. The remaining subjects are at an infinitely lower risk during days 1 to 6 and accumulate no hazard then, with subject 6 being credited with 1 unit of hazard at the last event. The residuals are thus 1 − 1/3 = 2/3, 0 − 1/3, 1 − 7/3 = −4/3, 1 − 0, 0, and 0, respectively, for the six subjects.

Values for the score and Schoenfeld residuals can be derived similarly as the limit as r →∞ of the formulae in Section 1.1.