Лемма о возрастании модуля многочлена. Лемма Даламбера. Основная теорема и следствия из нее. Рациональные дроби

Случайно, однако, это число может оказаться корнем для f' (х), а также, быть может, для некоторых из дальнейших производных. Пусть К-я производная (К» 1) будет первой, не имеющей хо своим корнем, т. е.

                    (хо)           (хо) =

Такое К существует, так как, если ао есть старший коэффициент многочлена г (х), то

Таким образом,

                                                                                                            Ч-             (хо).

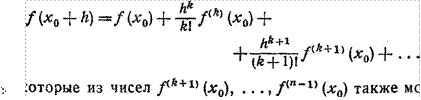также могут равняться нулю, но это для нас несущественно.

Деля обе части этого равенства на г (хо), отличное, по условию, от нуля, и вводя обозначение t(j) (ХО)  п, мы получим:

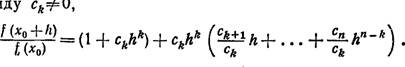или, ввиду

.f (хо Ч-

Переходя к модулям, получим:

                      (5)

До этого момента мы не делали никаких предположений о приращении И. Теперь мы будем выб и рать Ь, причем будем отдельно выбирать его модуль и его аргумент. Модуль будет выбираться следующим образом. Так как

4+1 И +

является многочленом от Ь без свободного члена, то, по лемме 1 полагая 8=—-       можно найти такое 61, что при lhl     будет

                                                                        (6)

С другой стороны, при

будет

                                                                                                             (7)

Положим, что модуль h выбран в соответствии с неравенством lhl <min (61, 62).     (8)

Тогда, ввиду (6), неравенство (5) превращается в строгое неравенство

 (хо + h)

                                                                                                                                (9)

условием (7) мы воспользуемся лишь позже, для выбора аргумента h потребуем, чтобы число Ckh^k было отрицательным действительным числом. Иными словами,

arg (СА^К) — arg ск Ч- К arg h = л, откуда л— аш ск

                                                                                                                           (10)

1 54                                                                                                                              

При этом выборе 12 число ск1Р будет отличаться знаком от своей абсолютной Величины,

-—l ске 1, а поэтому, используя неравенство (7),

= 1 1 -—1 скит — 1 -—1 ск1В 1.

Таким образом, при выборе на основании условий (8) и (10) неравенство (9) принимает вид

т. е. тем более

откуда следует

lf(xo+h)  1,

что доказывает лемму Даламбера.

При помощи той геометрической иллюстрации, которая была дана выше, можно следующим образом пояснить лемму Даламбера. Дано, что lf(xo) О. Это значит, что длина перпендикуляра, восставленного к комплексной плоскости в точке хо, отлична от нуля. Тогда, по лемме Даламбера, можно найти такую точку =Xo+h, что lf(X1)  l, т. е. перпендикуляр в точке будет более коротким, чем в точке хо, и, следовательно, поверхность, образованная концами перпендикуляров, будет в этой новой точке несколько ближе к комплексной плоскости. Как показывает доказательство леммы, модуль h можно считать сколь угодно малым, т. е. точку х1 можно выбрать как угодно близко к точке хо; мы не будем, однако, пользоватЬся в дальнейшем этим замечанием.

Корнями многочлена f(x) будут служить, очевидно, те комплексные числа (т. е. те точки комплексной плоскости), в которых поверхность, образованная концами перпендикуляров, коснется этой плоскости. Опираясь лишь на лемму Даламбера, нельзя доказать существование таких точек. В самом деле, пользуясь этой леммой, можно найти такую бесконечную последовательность точек хо, Х1, Х2,     что lf (хо)            lf(X1)    lf(X2)    .              (11)

Отсюда не следует, однако, существование такой точки х, что тем более, что убывающая последовательность положительных действительных чисел (11) вовсе не обязана стремиться к нулю.

Дальнейшие рассмотрения будут основаны на одной теореме из теории функций комплексного переменного, обобщающей теорему Вейерштрасса, известную читателю из курса математического анализа. Она относится к действительным функциям комплексного: переменного, т. е. к функциям КОМплеКСНOГО переменного, принимающим лишь действительные значения; примером таких функций служит модуль многочлена. В формулировке этой теоремы мы будем говорить для простоты о залжнутол круге Е, понимая под этим круг на комплексной плоскости, к которому присоединены все точки его границы.

Если Действительная функция g(x) комплексного переженного х непрерывна во всех точках замкнутого круга Е) то существует в круге Е такая точка хо, что для всех х из Е имеет лесто неравенство g(x) (хо). Точка хо является, СмДовательно, точкой жинилула для g(x) в круге Е.

Доказательство этой теоремы можно найти во всех курсах тео•