Собственные колебания консервативной системы с одной степенью свободы вблизи положения устойчивого равновесия. Свободные и затухающие колебания

Федеральное агентство по образованию

Государственное образовательное учреждение высшего профессионального образования

Санкт-Петербургский государственный горный институт им. Г.В. Плеханова

(технический университет)

РАСЧЕТНО-ГРАФИЧЕСКОЕ ЗАДАНИЕ № 1

	Теория колебаний

 

По дисциплине  __________________________________________________________

________________________________________________________________________

^{(наименование учебной дисциплины согласно учебному плану)}

ПОЯСНИТЕЛЬНАЯ ЗАПИСКА

Собственные колебания консервативной системы с одной степенью свободы вблизи положения устойчивого равновесия

Тема:

________________________________________________________________________

________________________________________________________________________

________________________________________________________________________

	РТ-03

 

Автор: студент гр.   _______         ____________________           /_______________/

^{(подпись)                                   (Ф.И.О.)}

Вариант № 12

ОЦЕНКА:    ______________

ДАТА: ___________________

ПРОВЕРИЛ

	профессор		Л.К.

 

Руководитель проекта    _________    ________________            /________________/

            ^{(должность)                       (подпись)                                                      (Ф.И.О.)}

Санкт-Петербург

2006

Расчетно-графическое задание подразделяется на 2 части:

I. Свободные колебания;

II. Затухающие колебания.

Часть I

Свободные колебания

Дано:

1. Схема колебательной системы (рис.1)

2. Начальные условия:

 - начальная координата;

 - начальная скорость.

3. Размеры отдельных элементов:

4. Массы отдельных элементов:

5. Жесткость пружины с.

Определить:

1. Выражение для потенциальной (П) и кинетической (Т) энергий системы.

2. Производные от потенциальной и кинетической энергий и подстановка их в уравнение Лагранжа.

3. Дифференциальное уравнение свободных колебаний системы.

4. Закон колебаний (интеграл от дифференциального уравнения) в двух формах.

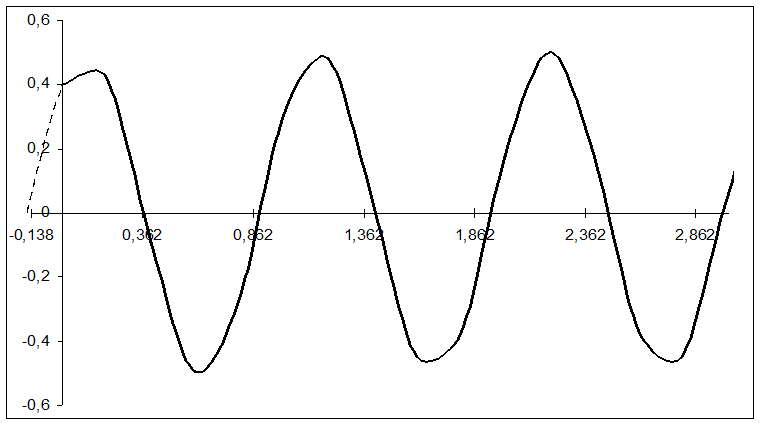
5. Построить график колебаний и записать параметры колебаний.

Исходные данные

Таблица 1

№ п/п
	кг	кг	кг	м	м	м	Н/м	м	м	м/с
1	2	3	4	5	6	7	8	9	10	11	12
12	25	36	9	4	6	5	4374	90	0,4	1,8	8

Схема колебательной системы

η0

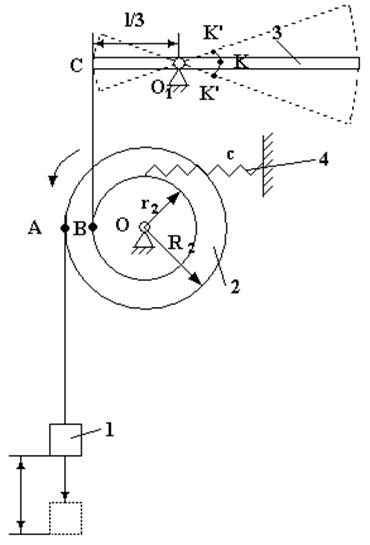
Рис.1

1 – груз массы , прикрепленный в точке А к свисающей с блока нити;

2 – бицилиндр массы  с радиусами ,  и радиусом инерции  относительно его геометрической оси;

3 – тонкий однородный стержень (планка) массы  и длины ;

4 – пружина жесткостью с.

Решение

Система имеет одну степень свободы. За обобщенную координату примем вертикальное отклонение  груза 1 от положения статического равновесия вниз. Все задаваемые силы, приложенные к системе, имеют потенциал, поэтому уравнение Лагранжа можно записать в форме:

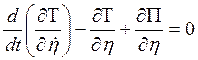, где

t – время;

 - соответственно обобщенные координата и скорость.

Определение кинетической энергии системы

Кинетическая энергия всей рассматриваемой системы                

                                                                                             (1)                                                                                                      

Груз 1 движется поступательно, поэтому его кинетическая энергия равна

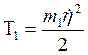 - энергия возвратно-поступательного движения груза 1.

Бицилиндрический блок 2 вращается вокруг неподвижной оси  с угловой скоростью 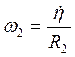. Радиус инерции блока известен, поэтому . Поэтому кинетическая энергия блока равна

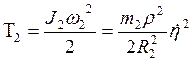 - энергия вращения вокруг неподвижной оси, где

 - момент инерции бицилиндра относительно оси ;

 - угловая скорость вращения бицилиндра.

Стержень 3 вращается вокруг неподвижной оси . Значит

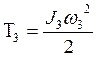 - кинетическая энергия вращения планки вокруг оси .  

Момент инерции стержня относительно оси, не проходящей через его конец .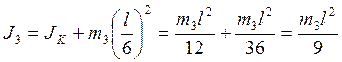

Для нахождения угловой скорости стержня  рассмотрим точки В и С, которые движутся практически с одинаковыми скоростями (вследствие малости рассматриваемых колебаний). Тогда 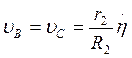. Отсюда искомая угловая скорость .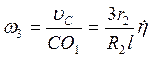

Поэтому кинетическая энергия вращения стержня равна

.

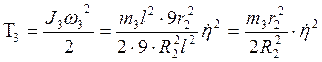В соответствии с формулой (1) кинетическая энергия всей рассматриваемой системы

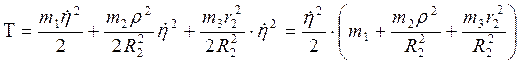
Введем обозначение обобщенного инерционного коэффициента (обобщенной массы системы) .

Заметим, что .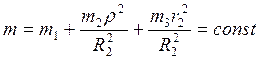

После преобразований формула кинетической энергии системы примет следующий вид

.

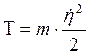Вычислим обобщенную массу системы

.

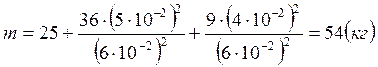В результате получим для кинетической энергии всей системы .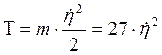

Определение потенциальной энергии системы

Потенциальная энергия системы определяется работой сил тяжести системы и силы упругости пружины на перемещении системы из отклоненного положения, когда груз 1 имеет координату , в положение статического равновесия. При таком отклонении вес блока работы не производят, поэтому потенциальная энергия всей системы равна

,                                                (2)

где  - потенциальная энергия пружины.

Очевидно, потенциальная энергия груза 1 равна  (примем g = 10 м/с²). Знак минус ставится потому, что груз 1 из положения статического равновесия отклоняется вниз при положительном .

Аналогично (рис.2) потенциальная энергия стержня равна , где h – смещение центра тяжести планки вверх.

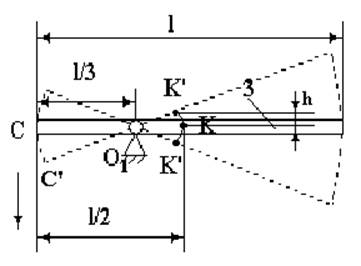
Рис.2

Легко видеть, что 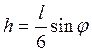. Ввиду того, что мы рассматриваем малые колебания системы, угол  весьма мал и, следовательно, синус в последнем выражении можно заменить соответствующим углом. Тем самым в разложении синуса в ряд сохраняется лишь один член. В теории малых колебаний большая точность не нужна, ибо потенциальную энергию необходимо вычислять с точностью до величин второго порядка малости относительно обобщенной координаты. Таким образом, 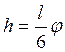. Для нахождения центрального угла дуги KK’  рассмотрим перемещение планки в точку С’.

 

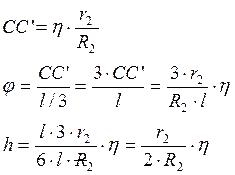
Следовательно, потенциальная энергия стержня равна

.

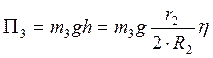Потенциальная энергия пружины равна 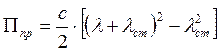, где

 - динамическая деформация пружины;

- статическая деформация пружины.

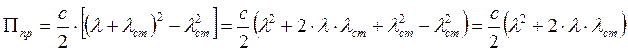, где

 - растяжение пружины при движении груза 1 вниз.

.

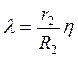После подстановки и преобразования получим

.

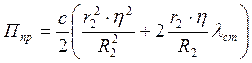В соответствии с формулой (2) потенциальная энергия всей системы равна

.

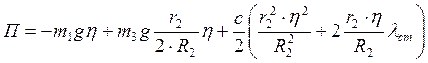
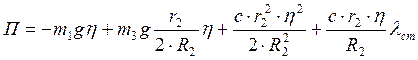В положении, соответствующем , система находится в равновесии. Поэтому должно выполняться условие: 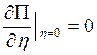. Тогда

.

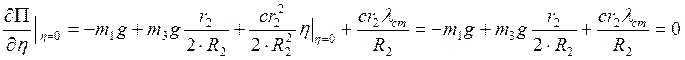Преобразуем выражение для полной потенциальной энергии

 

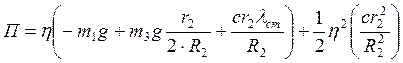
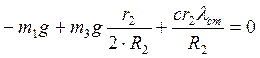
Обозначим выражени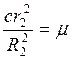е , где

μ – обобщенная жесткость системы, Н/м.  

.

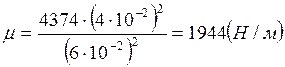Таким образом, потенциальная энергия всей системы равна

.

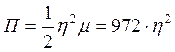Полные кинетическая и потенциальная энергии системы

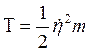
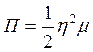
Уравнение Лагранжа

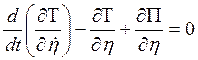
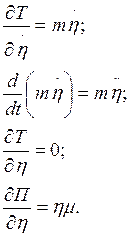
Дифференциальное уравнение свободных колебаний системы

Разделим дифференциальное уравнение колебаний на m

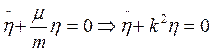, где

k – круговая частота колебаний, рад/с.

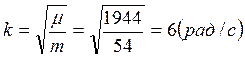
Закон колебаний

(интеграл от дифференциального уравнения) в двух формах

I форма закона колебаний:

, где с_1,2 – постоянные интегрирования.

.

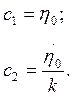
II форма закона колебаний:

, где

a – неизвестная амплитуда колебаний.

α – неизвестная начальная фаза колебаний.

 

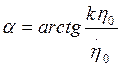
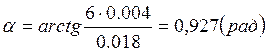
Начальная фаза, выраженная через время t, .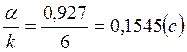

Период колебаний .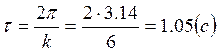

Абсолютная частота колебаний .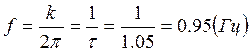

Размах колебаний .

Параметры свободных колебаний

1. Начальная координата

2. Начальная скорость

3. Начальная фаза  

4. Фаза колебаний

5. Амплитуда колебаний

6. Размах колебаний

7. Период колебаний

8. Частоты колебаний:

8.1. Круговая частота

8.2. Абсолютная частота

τ

График свободных колебаний

a

-a

Часть II

затухающие колебания

Исследование затухающих колебаний проведем на той же схеме