Для функции ![]() , имеющей все производные до
, имеющей все производные до ![]() -го порядка включительно, в
окрестности точки
-го порядка включительно, в
окрестности точки ![]() справедлива формула Тейлора
/5/:
справедлива формула Тейлора
/5/:
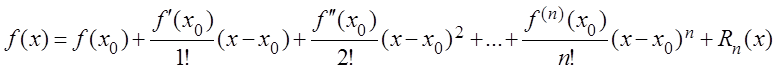 . (3.20)
. (3.20)
Остаточный член
формулы Тейлора ![]() может быть вычислен по
формуле:
может быть вычислен по
формуле:
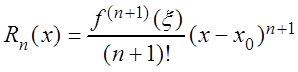 ,
(3.21)
,
(3.21)
где
![]() – некоторая точка между
– некоторая точка между ![]() и
и ![]() ,
т.е.
,
т.е. ![]() для некоторого
для некоторого ![]() .
.
При ![]() формула (3.20) называется формулой
Маклорена.
формула (3.20) называется формулой
Маклорена.
Если функция ![]() имеет производные всех порядков в
окрестности точки
имеет производные всех порядков в
окрестности точки ![]() , то в формуле Тейлора
(3.20) число
, то в формуле Тейлора
(3.20) число ![]() можно брать сколь угодно большим. Допустим,
что в рассматриваемой окрестности остаточный член
можно брать сколь угодно большим. Допустим,
что в рассматриваемой окрестности остаточный член ![]() стремится
к нулю при
стремится
к нулю при ![]() , т.е.
, т.е. ![]() .
Тогда, переходя в формуле (3.20) к пределу при
.
Тогда, переходя в формуле (3.20) к пределу при ![]() ,
получим справа бесконечный ряд, который называется рядом Тейлора:
,
получим справа бесконечный ряд, который называется рядом Тейлора:
 (3.22)
(3.22)
При ![]() получаем ряд, который называется рядом
Маклорена:
получаем ряд, который называется рядом
Маклорена:
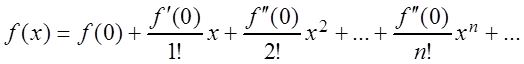 (3.23)
(3.23)
Формулы (3.22)
и (3.23) справедливы лишь в том случае, если ![]() при
при
![]() . В этом случае ряды справа сходятся
и их сумма равна данной функции
. В этом случае ряды справа сходятся
и их сумма равна данной функции ![]() . Докажем, что это
действительно так.
. Докажем, что это
действительно так.
Теорема 3.5.
Для того чтобы ряд Тейлора (3.22) сходился на ![]() и
имел своей суммой функцию
и
имел своей суммой функцию ![]() , необходимо и
достаточно, чтобы на
, необходимо и
достаточно, чтобы на ![]() остаточный член
остаточный член ![]() формулы Тейлора (3.20) стремился к
нулю при
формулы Тейлора (3.20) стремился к
нулю при ![]() , т.е.
, т.е. ![]() для
любого
для
любого ![]() .
.
Доказательство
1)
Необходимость. Пусть функция ![]() – сумма ряда
Тейлора на
– сумма ряда
Тейлора на ![]() , т.е.
, т.е. ![]() ,
где
,
где ![]() –
– ![]() -я
частичная сумма ряда (3.20).
-я
частичная сумма ряда (3.20).
Формулу Тейлора (3.20) можно представить в виде:
![]() ,
(3.24)
,
(3.24)
где ![]() -й
остаток ряда
-й
остаток ряда ![]() определяется формулой (3.21). Из
равенства (3.24) следует, что
определяется формулой (3.21). Из
равенства (3.24) следует, что ![]() для любого
для любого ![]() .
.
2) Достаточность.
Пусть ![]() для любого
для любого ![]() .
Тогда из равенства (3.24) следует, что
.
Тогда из равенства (3.24) следует, что ![]() ,
т.е.
,
т.е. ![]() . А это означает, что ряд Тейлора
(3.22) сходится на интервале
. А это означает, что ряд Тейлора
(3.22) сходится на интервале ![]() , и его сумма для
любого x из этого интервала равна:
, и его сумма для
любого x из этого интервала равна: ![]() .
.
Из
доказательства теоремы 3.4 следует, что если функция ![]() разлагается
в ряд Тейлора (степенной ряд), то это разложение единственное.
разлагается
в ряд Тейлора (степенной ряд), то это разложение единственное.
Если ![]() , то ряд не представляет данной
функции, хотя может и сходиться (к другой функции). Поэтому, для того чтобы
доказать, что формально выписанный ряд Тейлора сходится к данной функции, нужно
доказать, что остаточный член стремится к нулю.
, то ряд не представляет данной
функции, хотя может и сходиться (к другой функции). Поэтому, для того чтобы
доказать, что формально выписанный ряд Тейлора сходится к данной функции, нужно
доказать, что остаточный член стремится к нулю.
Рассмотрим разложение в ряд Маклорена некоторых элементарных функций.
Пример 3.
Разложить в ряд Маклорена функцию: ![]() .
.
Решение.
Найдём производные функции ![]() и вычислим их
при
и вычислим их
при ![]() :
:
![]() ,
, ![]() ,
…,
,
…, ![]() , …
, …
Значит, ![]() ,
, ![]() ,
…,
,
…, ![]() , … В результате, получаем ряд:
, … В результате, получаем ряд:
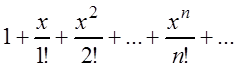 (3.25)
(3.25)
Покажем, что
полученный ряд сходится к функции ![]() . Найдём интервал
сходимости степенного ряда (3.25):
. Найдём интервал
сходимости степенного ряда (3.25):
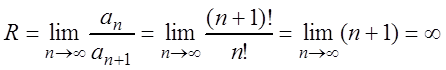 ,
,
следовательно, ряд (3.25) абсолютно сходится на всей числовой прямой.
Докажем теперь,
что функция ![]() – сумма ряда (3.25). Остаточный член
– сумма ряда (3.25). Остаточный член
 ,
,
где число ![]() лежит
между 0 и
лежит
между 0 и ![]() . Отсюда следует, что
. Отсюда следует, что
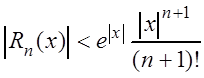 .
(3.26)
.
(3.26)
Так как ряд
(3.25) сходится, то используя необходимый признак сходимости ряда (теорема
3.1), можно записать: 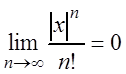 , тогда и
, тогда и 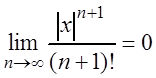 .
.
Поэтому,
переходя к пределу в неравенстве (3.26) при ![]() ,
получаем, что
,
получаем, что
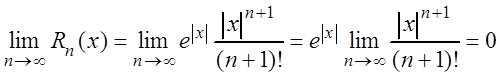
при любом ![]() и, следовательно, функция
и, следовательно, функция ![]() является суммой ряда (3.25).
является суммой ряда (3.25).
Таким образом, при любом ![]() имеет место разложение:
имеет место разложение:
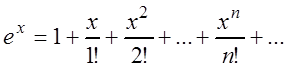
В общем случае
разложение в степенные ряды основано на использовании рядов Тейлора или
Маклорена. Но на практике степенные ряды многих функций можно найти формально,
используя известные разложения (например, как для функции ![]() ) или формулу для суммы членов
геометрической прогрессии. Иногда при разложении полезно пользоваться почленным
дифференцированием или интегрированием рядов. В интервале сходимости ряды сходятся
к соответствующим функциям.
) или формулу для суммы членов
геометрической прогрессии. Иногда при разложении полезно пользоваться почленным
дифференцированием или интегрированием рядов. В интервале сходимости ряды сходятся
к соответствующим функциям.
Пример 4. Разложить в ряд Маклорена функцию: f(x) = chx.
Решение.
Так как chx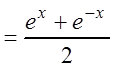 , то воспользуемся
разложением:
, то воспользуемся
разложением:
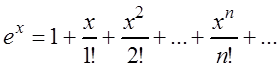
![]() ,
,
где вместо ![]() подставляем
подставляем ![]() , тогда
, тогда
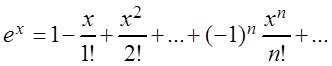
Полученный ряд сходится при любых ![]() .
.
Теперь найдём разложение функции chx:
chx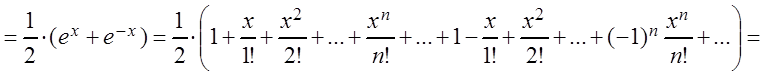
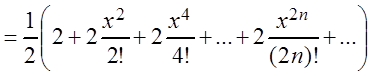 .
.
Таким образом,
chx  ,
,
причём ряд сходится при любом ![]() .
.
Пример 5.
Рассмотрим ряд: ![]() Данный ряд является суммой
членов геометрической прогрессии с первым членом
Данный ряд является суммой
членов геометрической прогрессии с первым членом ![]() и
знаменателем
и
знаменателем ![]() . Как известно, при
. Как известно, при ![]() данный ряд сходится и его сумма
равна
данный ряд сходится и его сумма
равна  . Следовательно,
. Следовательно,
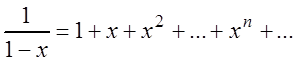 (3.27)
(3.27)
Данное равенство является
разложением функции 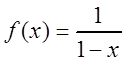 в степенной ряд (ряд
Маклорена) на интервале
в степенной ряд (ряд
Маклорена) на интервале ![]() .
.
Пример 6. Рассмотрим функцию 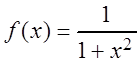 . Используя
разложение (3.27), можно записать:
. Используя
разложение (3.27), можно записать:
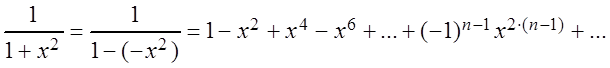
Полученный ряд сходится при ![]() , значит, его можно почленно интегрировать
на любом отрезке
, значит, его можно почленно интегрировать
на любом отрезке ![]() . Следовательно,
. Следовательно,
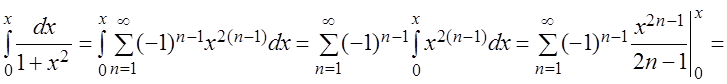
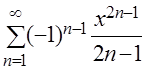 .
.
С другой стороны,
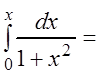 arctg
arctg![]() arctg x,
arctg x,
поэтому
arctg x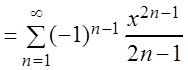 ,
,
т.е. получили ряд Маклорена,
сходящийся к данной функции при ![]() . Можно доказать,
что ряд сходится и для
. Можно доказать,
что ряд сходится и для ![]() , и что для обоих этих
значений сумма ряда равна arctg x.
, и что для обоих этих
значений сумма ряда равна arctg x.
Пример 7.
Разложить функцию: ![]() в ряд Маклорена.
в ряд Маклорена.
Решение. Найдём производные:
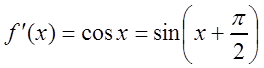 ,
, 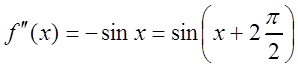 ,
…,
,
…, 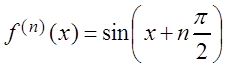 ,
,
откуда, полагая ![]() , получаем:
, получаем:
![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
![]() , …
, …
Составим по формуле (3.23) ряд Маклорена:
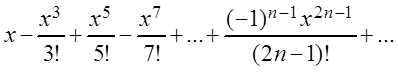 (3.28)
(3.28)
Найдём радиус сходимости степенного ряда (3.28):
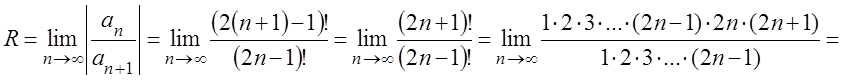
![]() ,
,
т.е. ряд (3.28) сходится абсолютно при любом ![]() . Исследуем остаточный член:
. Исследуем остаточный член:
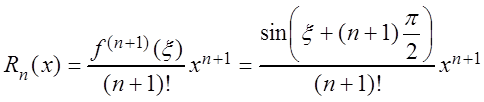 ,
,
где ![]() ,
, ![]() . Так как
. Так как 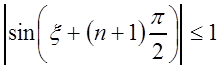 ,
то
,
то 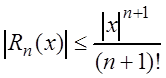 . А так как
. А так как 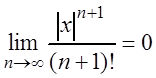 (см.
пример 3), то
(см.
пример 3), то ![]() при любом
при любом ![]() . Следовательно,
. Следовательно,
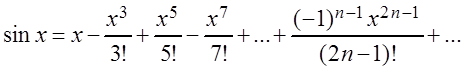 ,
,
т.е. получили ряд, сходящийся к
функции ![]() при любом
при любом ![]() .
.
Аналогично
можно получить разложение функции ![]() в ряд Маклорена,
справедливое при любом
в ряд Маклорена,
справедливое при любом ![]() . Однако ещё проще
разложение
. Однако ещё проще
разложение ![]() получается почленным дифференцированием
ряда для
получается почленным дифференцированием
ряда для ![]() :
:
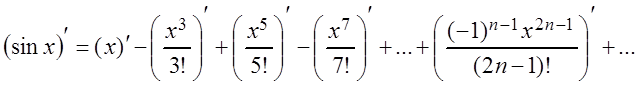
откуда
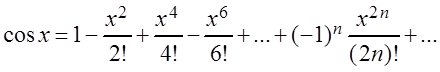
Аналогично можно получить разложения в степенные ряды многих других функций. Выпишем ряды Маклорена для некоторых элементарных функций, которые чаще всего используются в приближённых вычислениях:

![]() ,
(3.29)
,
(3.29)
chx 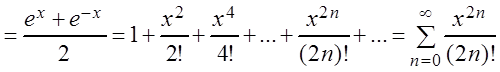
![]() , (3.30)
, (3.30)
shx 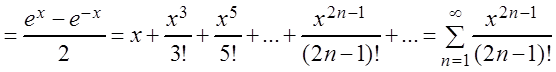
![]() , (3.31)
, (3.31)
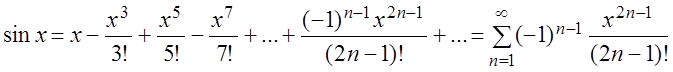
![]() , (3.32)
, (3.32)
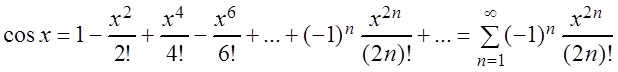
![]() , (3.33)
, (3.33)
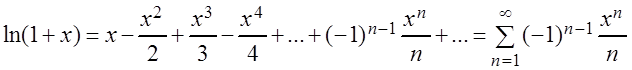
![]() , (3.34)
, (3.34)
arctgx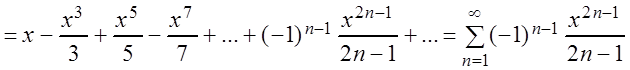
![]() , (3.35)
, (3.35)

![]() ,
(3.36)
,
(3.36)
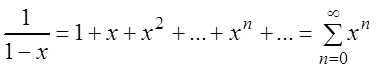
![]() ,
(3.37)
,
(3.37)
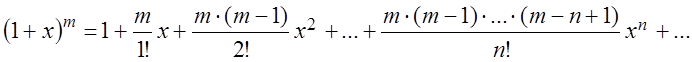
![]() .
(3.38)
.
(3.38)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.