Пример 1. Hайти общее решение уравнения y¢cosx – (y + 1)sinx = 0.
Решение.
Разделим переменные. Для этого умножим обе части уравнения на множитель 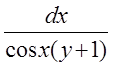 , заменив y¢ на
, заменив y¢ на ![]() Уравнение примет вид:
Уравнение примет вид: 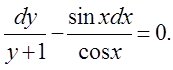
Проинтегрируем почленно это уравнение, получим:
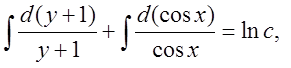
![]()
![]()
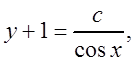
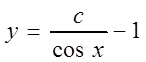 ,
,
получили общий интеграл уравнения.
Пример 2. Найти частное решение
уравнения: ![]() если y = 3 при x = 1.
если y = 3 при x = 1.
Решение. Перепишем
уравнение в виде: 2ydy = (1 – 3x2)dx,
заменив y¢ на ![]()
Интегрируя обе части уравнения, получим:
![]()
![]()
–
общий интеграл уравнения. Подставим начальные условия y = 3 при x =
1, получим:
9 = 1 – 1 + c, отсюда следует, что c = 9. Искомое частное решение
имеет вид:
y2 = x – x3 + 9 или x3 + y2 – x – 9 = 0.
Пример. Проинтегрировать уравнение: 2x2dy = (x2 + y2) dx .
Решение.
Разделив обе части уравнения на x2dx, получим уравнение, правая часть которого есть
функция отношения ![]() :
:
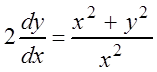 или
или 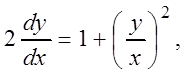
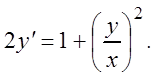
Положим в нем 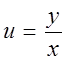 ,
тогда y = ux, дифференцируем
,
тогда y = ux, дифференцируем ![]() получим
уравнение с разделяющимися переменными:
получим
уравнение с разделяющимися переменными:
![]()
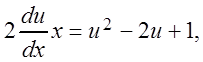
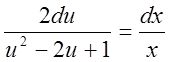 .
.
После разделения переменных получим уравнение с разделенными переменными:
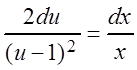 .
.
Интегрируем
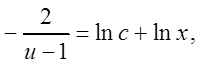 подставим
подставим 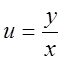 ,
получим:
,
получим:
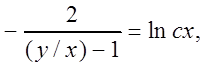
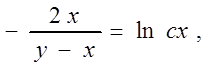
![]()
Замечание. При разделении переменных мы делили на x и на (u – 1)2, что возможно лишь при x ¹ 0 и u ¹ 1. Непосредственной проверкой легко убедиться, что x = 0 и u = 1 т. е. y = x , являются также решениями данного уравнения, но они не входят в общий интеграл. Такие решения называются особыми.
Пример 1.
Найти общее решение уравнения: ![]() .
.
Решение. Поделим обе части данного уравнения на (1 + x2), получим:
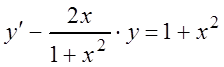
–
линейное уравнение. Решим его, применяя метод подстановки y = u×v, тогда ![]() Подставим значения y и y¢ в данное уравнение:
Подставим значения y и y¢ в данное уравнение:
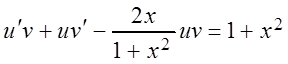 ,
,
сгруппируем члены:
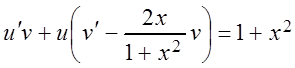 . (4.1)
. (4.1)
Выберем функцию v так, чтобы выражение в скобках было равно нулю:
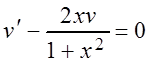 .
.
Тогда уравнение (4.1) запишем в виде системы уравнений:
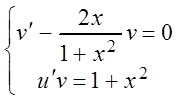 . (4.2)
. (4.2)
Найдем функцию v из первого уравнения системы:
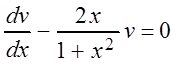 ,
,
разделим переменные:
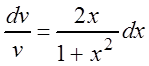 .
.
Интегрируя, получаем: ![]() , пусть с1 = 1, v
= 1 + x2.
, пусть с1 = 1, v
= 1 + x2.
Подставим значение функции v во второе уравнение системы (4.2):
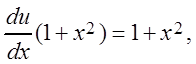
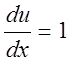 ,
, ![]() ,
откуда u = x + с.
,
откуда u = x + с.
Найденные функции u и v подставим в равенство y = u×v, получим:
y = (1 + x2)(x + с)
– общее решение данного уравнения.
Рассмотрим задачу, приводящую к дифференциальному уравнению.
Пример 2. Найти кривую, проходящую через точку M0(1, 4) и обладающую тем свойством, что отрезок любой ее касательной, заключенный между осями координат, делится пополам в точке касания.
Решение. Сделаем чертеж (рис. 4.1). Пусть M(x, y) – произвольная точка искомой кривой, AB – отрезок касательной к кривой в данной точке, заключенный между координатными осями. По условию задачи BM = MA. Если OP – абсцисса точки M, то DAMP ~ DABO и
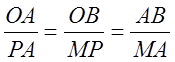 .
.
Но
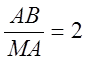 , PA = OP,
поэтому
, PA = OP,
поэтому 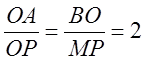 , т.е. OA
= 2x, OB = 2y.
, т.е. OA
= 2x, OB = 2y.
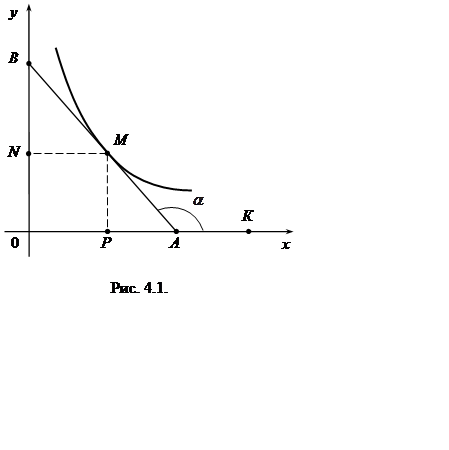 Угловой коэффициент касательной к кривой y = ¦(x) в точке M(x, y) выражается с помощью производной:
Угловой коэффициент касательной к кривой y = ¦(x) в точке M(x, y) выражается с помощью производной:
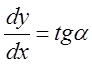 , где a = ÐBAК.
, где a = ÐBAК.
С другой стороны, так как
![]() и
и 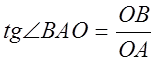 ,
,
то
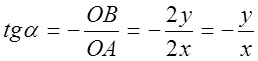 .
.
Следовательно, 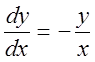 –
дифференциальное уравнение с разделяющимися переменными. Разделим переменные
–
дифференциальное уравнение с разделяющимися переменными. Разделим переменные 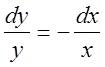 , интегрируем:
, интегрируем:
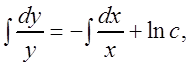
![]() ,
, ![]() .
.
Так как кривая должна проходить через точку M0(1, 4),
то подставляя ее координаты в данное уравнение, находим: 1×4 = с, с = 4. Таким образом, искомая кривая определяется
уравнением ![]() .
.
Пример 3. Лодка замедляет свое движение под действием сопротивления воды, которое пропорционально скорости лодки. Начальная скорость лодки 1,5 м/с, через 4 с скорость ее 1 м/с. Найти скорость движения лодки через 12 с после начала движения.
Решение. Согласно второму закону динамики дифференциальное уравнение движения имеет вид:
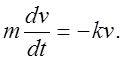
Это дифференциальное уравнение с разделяющимися переменными. Разделяя переменные, получим:
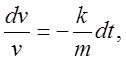
интегрируем:
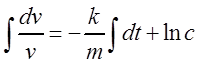 ,
, 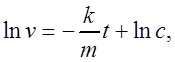
![]()
Подставляя
начальные условия: ![]() ,
, ![]() находим:
находим:
![]() ; с
= 1,5.
; с
= 1,5.
Следовательно, ![]() .
Значение k/m определим, подставляя второе начальное условие: t =
4, v = 1,
.
Значение k/m определим, подставляя второе начальное условие: t =
4, v = 1, ![]() . Отсюда следует:
. Отсюда следует: 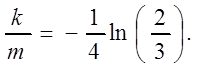 Итак, получили частное решение
данного уравнения:
Итак, получили частное решение
данного уравнения:
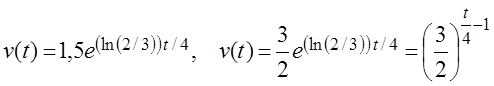 .
.
Подставим в это равенство t = 12, окончательно получим:
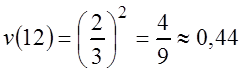 .
.
Пример 1.
Проинтегрировать уравнение: 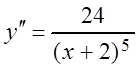 .
.
Решение. Интегрируем это уравнение последовательно два раза:
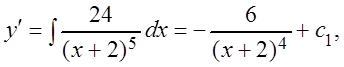
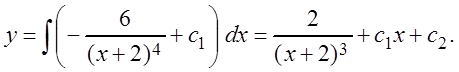
Пример 2.
Найти общее решение уравнения: ![]()
Решение. Это
уравнение не содержит явно искомой функции y. Положив в уравнении y¢= z, y² = z¢, получим
линейное уравнение первого порядка относительно z(x): ![]() . Заменив z = uv, z¢ = u¢v + uv¢, получим:
. Заменив z = uv, z¢ = u¢v + uv¢, получим:
u¢v + uv¢ + uvtgx = sin2x, u¢v + u (v¢ + vtgx) = sin2x.
Это уравнение заменим системой уравнений:
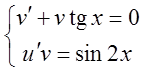 .
.
Решаем первое уравнение системы:
![]()
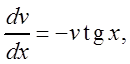
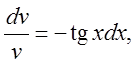
интегрируем: 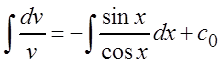 ,
с0 = 0, откуда
,
с0 = 0, откуда ![]() или
или ![]() Подставим найденное значение v
во второе уравнение системы:
Подставим найденное значение v
во второе уравнение системы: ![]()
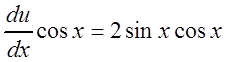 . Разделим переменные
. Разделим переменные ![]() интегрируем:
интегрируем: ![]() ,
следовательно,
,
следовательно, ![]() Возвращаясь к первоначальной
переменной y, получим:
Возвращаясь к первоначальной
переменной y, получим:
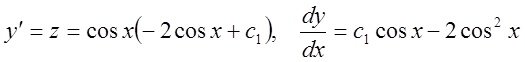 .
.
Разделим
переменные ![]() , интегрируем:
, интегрируем:
![]()
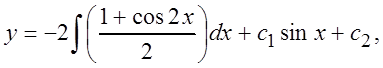
получим общее решение данного уравнения:
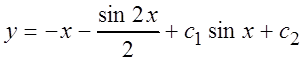
Пример 3.
Найти общее решение уравнения: ![]()
Решение. Это дифференциальное уравнение не содержит в явном виде независимую переменную x. Положим y¢ = p, y² = p(dp/dy), подставим в данное уравнение:
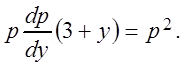
Разделим
переменные 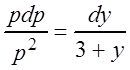 или
или 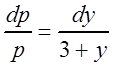 , интегрируем:
, интегрируем:
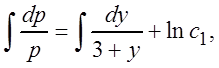
![]() ,
, ![]() .
.
А так как p = y¢, то получим y¢ = c1(3 + y)
– уравнение первого порядка с разделяющимися переменными. Разделим их: 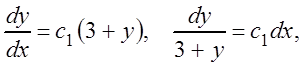 интегрируем:
интегрируем:
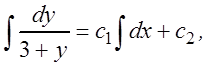
![]() ,
, ![]() ,
,
![]() .
.
Получили общее решение данного уравнения.
Для нахождения частного решения линейного неоднородного уравнения используется метод неопределенных коэффициентов. Частное решение линейного неоднородного уравнения для правых частей специального вида может быть найдено по виду правой части. Запишем в таблицу наиболее часто встречающиеся случаи (табл. 4.1).
|
Правая часть дифференциального уравнения |
Корни характеристического |
Вид частного |
|
1)
где |
а) Число 0 не является корнем характеристического уравнения |
|
|
б) Число 0 является корнем характеристического уравнения кратности s |
|
|
|
2) |
а) Число a не является корнем характеристического уравнения |
|
|
б) Число a является корнем характеристического уравнения кратности s |
|
|
|
3)
|
а) Число bi не является корнем характеристического уравнения |
где
|
|
б) Число bi является корнем характеристического уравнения |
где
|
Пример 1.
Найти частное решение уравнения ![]() , удовлетворяющее
начальным условиям y(0) = 1, y¢(0) = 0.
, удовлетворяющее
начальным условиям y(0) = 1, y¢(0) = 0.
Решение.
Запишем соответствующее однородное уравнение: ![]() ,
характеристическое уравнение имеет вид:
,
характеристическое уравнение имеет вид: ![]() ,
его корни
,
его корни ![]() k2 = 2.
k2 = 2.
Общее решение однородного уравнения:
![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.