Все возможные значения случайной величины m разбиваются на l обычно равных
интервалов: ![]() , покрывающих всю выборку …
, покрывающих всю выборку …
Строится величина
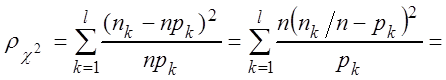 n
n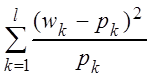 ,
,
где ![]() – вероятность
попадания варианты в k-й интервал,
– вероятность
попадания варианты в k-й интервал, ![]() –
предполагаемая теоретическая функция распределения.
–
предполагаемая теоретическая функция распределения.
Независимо от F0(x)
случайная величина имеет ![]() -распределение
с (l – 1) степенями свободы. Если F0(x)
зависит от одного или нескольких параметров и эти параметры оцениваются по
данным случайной выборки, то число степеней свободы уменьшается на число этих
параметров. Поэтому число степеней свободы определяется по формуле
-распределение
с (l – 1) степенями свободы. Если F0(x)
зависит от одного или нескольких параметров и эти параметры оцениваются по
данным случайной выборки, то число степеней свободы уменьшается на число этих
параметров. Поэтому число степеней свободы определяется по формуле ![]() , где r – число параметров
распределения, оцененных по выборке.
, где r – число параметров
распределения, оцененных по выборке.
Критерий ![]() (Мизеса)
(Мизеса)
Критерий Мизеса строится на основе статистики
![]() =
= 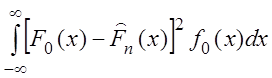 ,
,
здесь ![]() . При n ® ¥ величина r
=
. При n ® ¥ величина r
= ![]() распределена по закону
распределена по закону ![]()
rнабл = 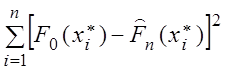 .
.
3.5. Доверительные интервалы
По результатам случайной выборки ![]() всегда можно построить точечную
оценку
всегда можно построить точечную
оценку ![]() . При точечном оценивании
мы не застрахованы от сколь угодно больших ошибок. Требуется определить
промежуток или интервал, которому принадлежит истинное значение параметра q. Как правило, с вероятностью равной единице, можно
утверждать лишь, что q может быть
любым из множества возможных значений, поэтому при построении промежутков
изменения параметра qзадаются некоторой вероятностью – доверительной
вероятностью, близкой к единице, и границы интервала (
. При точечном оценивании
мы не застрахованы от сколь угодно больших ошибок. Требуется определить
промежуток или интервал, которому принадлежит истинное значение параметра q. Как правило, с вероятностью равной единице, можно
утверждать лишь, что q может быть
любым из множества возможных значений, поэтому при построении промежутков
изменения параметра qзадаются некоторой вероятностью – доверительной
вероятностью, близкой к единице, и границы интервала (![]() ) выбирают из условия:
) выбирают из условия:
Р(![]() ) = g,
) = g,
где g –
доверительная вероятность (уровень доверия), (![]() )
– доверительный интервал вероятности g. Доверительная вероятность выбирается так, чтобы событие с вероятностью
появления g можно было
считать практически невозможным. В математической статистике обычно
используются доверительные вероятности из ряда: 0,9; 0,95; 0,99; 0,995; 0,999.
Выбор доверительной вероятности полностью зависит от исследователя, но с учетом
физической сути изучаемого явления. Так, например, степень доверия
авиапассажира к надежности самолета или парашютиста к надежности парашюта, несомненно,
должна быть выше степени доверия покупателя к надежности электрической лампочки
или даже утюга.
)
– доверительный интервал вероятности g. Доверительная вероятность выбирается так, чтобы событие с вероятностью
появления g можно было
считать практически невозможным. В математической статистике обычно
используются доверительные вероятности из ряда: 0,9; 0,95; 0,99; 0,995; 0,999.
Выбор доверительной вероятности полностью зависит от исследователя, но с учетом
физической сути изучаемого явления. Так, например, степень доверия
авиапассажира к надежности самолета или парашютиста к надежности парашюта, несомненно,
должна быть выше степени доверия покупателя к надежности электрической лампочки
или даже утюга.
Границы доверительных интервалов будем определять, опираясь на точечные оценки. По построенной точечной оценке доверительные интервалы можно определять различными способами. Наиболее часто на практике встречаются симметричные и односторонние доверительные интервалы:
Рассмотрим
схему построения симметричных доверительных интервалов, одно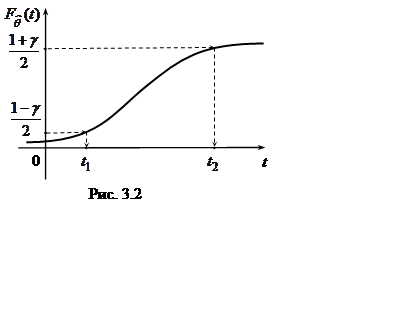 сторонние получаются аналогично.
сторонние получаются аналогично.
По данным выборки вычисляется "хорошая"
точечная оценка ![]() , которая является
случайной величиной. Для нее можно построить функцию распределения
, которая является
случайной величиной. Для нее можно построить функцию распределения ![]() .
.
Найдем t1 = t1(q) и t2 = t2(q) из уравнений:
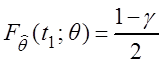 ,
, 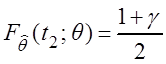 .
(3.4)
.
(3.4)
Таким образом, t1 и t2 – квантили уровней 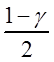 и
и 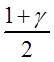 (рис. 3.2).
(рис. 3.2).
При этом
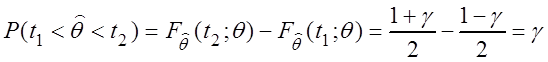 ;
;
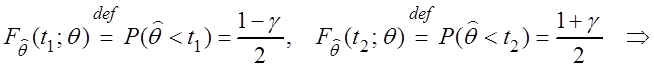
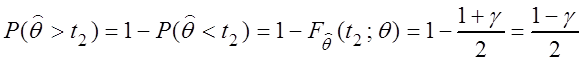 .
.
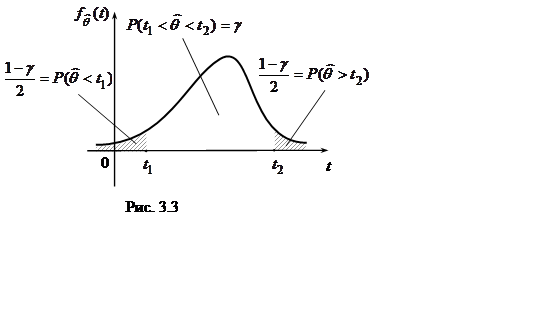 Таким образом, при заданном
Таким образом, при заданном ![]() оценка
оценка
![]() с вероятностью
с вероятностью ![]() заключена в интервале
заключена в интервале ![]() , причем вероятности попадания
случайной величины
, причем вероятности попадания
случайной величины ![]() , как левее, так и
правее, одинаковы и равны
, как левее, так и
правее, одинаковы и равны 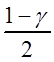 (отсюда
происходит название – симметричный интервал, рис. 3.3). Так как
(отсюда
происходит название – симметричный интервал, рис. 3.3). Так как ![]() , то, в силу принципа практической
достоверности события
, то, в силу принципа практической
достоверности события ![]() , все возможные
пары
, все возможные
пары ![]() будут принадлежать области
D между кривыми t1 = t1(q) и t2 = t2(q). Для
окончания построения доверительного интервала остается заметить, что, получив
по выборке оценку
будут принадлежать области
D между кривыми t1 = t1(q) и t2 = t2(q). Для
окончания построения доверительного интервала остается заметить, что, получив
по выборке оценку ![]() , мы вправе
сделать вывод, что неизвестный параметр должен лежать внутри интервала (
, мы вправе
сделать вывод, что неизвестный параметр должен лежать внутри интервала (![]() ), где
), где ![]() определяются
из уравнений:
определяются
из уравнений:
– для возрастающих функций ![]()
![]() , (3.5)
, (3.5)
формально ![]() .
.
– для убывающих функций ![]()
![]() ,
,
формально ![]() .
.
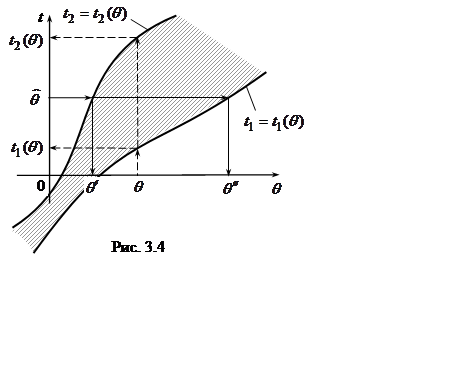 Схема построения
доверительного интервала, геометрическая интерпретация уравнений (3.5) и их
решений приведена на рис. 3.4.
Схема построения
доверительного интервала, геометрическая интерпретация уравнений (3.5) и их
решений приведена на рис. 3.4.
Пример 3.9. Построить доверительный интервал
доверительной вероятности ![]() для
среднего
для
среднего ![]() нормального распределения
с известной дисперсией
нормального распределения
с известной дисперсией ![]() .
.
Решение. "Хорошая" оценка для
параметра ![]() выборное среднее
выборное среднее  . Известно, что эта оценка
распределена по нормальному закону с параметрами:
. Известно, что эта оценка
распределена по нормальному закону с параметрами: ![]() .
Значит
.
Значит 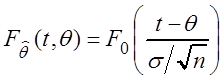 , где
, где ![]() – функция стандартного нормального
распределения, которая, в свою очередь, выражается через интегральную функцию
Лапласа
– функция стандартного нормального
распределения, которая, в свою очередь, выражается через интегральную функцию
Лапласа  .
.
Решим уравнения (3.4):
![]()
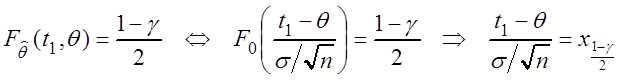
![]()
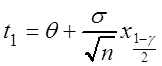 ,
,
где ![]() – квантиль уровня
– квантиль уровня
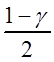 стандартного нормального
распределения, т.е. функция t1 = t1(q) здесь является линейной. Аналогично
стандартного нормального
распределения, т.е. функция t1 = t1(q) здесь является линейной. Аналогично
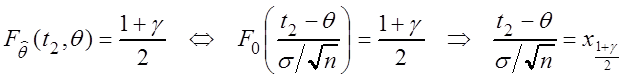
![]()
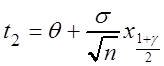 ,
,
 т.е. t2 = t2(q) тоже линейная функция. Теперь из первого уравнения (3.5)
находим
т.е. t2 = t2(q) тоже линейная функция. Теперь из первого уравнения (3.5)
находим ![]() :
:
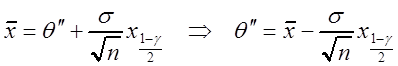 ,
,
а из второго уравнения (3.5) – ![]() :
:
 .
.
Для стандартного нормального распределения
 .
.
Квантиль ![]() определяется из
уравнения
определяется из
уравнения
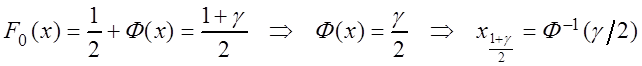 ,
,
где, при заданной доверительной вероятности ![]() , значение
, значение ![]() находится по таблице интегральной
функции Лапласа (приложение 2). Окончательно доверительный интервал имеет вид
находится по таблице интегральной
функции Лапласа (приложение 2). Окончательно доверительный интервал имеет вид
 . (3.6)
. (3.6)
Пример 3.10. Построить доверительный интервал
доверительной вероятности ![]() для
дисперсии
для
дисперсии ![]() нормального распределения
с известным средним
нормального распределения
с известным средним ![]() .
.
Решение. Рассмотрим оценку для дисперсии вида 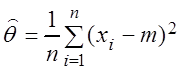 . Тогда случайная величина
. Тогда случайная величина 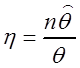 имеет
имеет ![]() -распределение
с
-распределение
с ![]() степенями свободы (см. подразд.
2.14) и значит
степенями свободы (см. подразд.
2.14) и значит
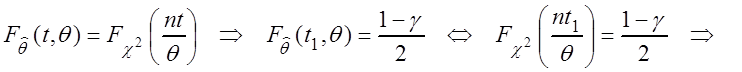
Þ 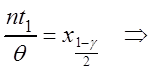
 ,
,
где ![]() – квантиль уровня
– квантиль уровня
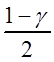
![]() -распределения
с
-распределения
с ![]() степенями свободы.
степенями свободы.
Аналогично
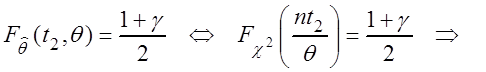
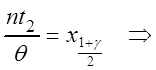
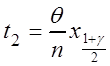 ,
,
где ![]() – квантиль уровня
– квантиль уровня

![]() -распределения
с
-распределения
с ![]() степенями свободы. Теперь из первого
уравнения (3.5) находим
степенями свободы. Теперь из первого
уравнения (3.5) находим ![]() :
: ![]()
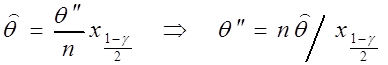 ,
,
а из второго уравнения (3.5) – ![]() :
:
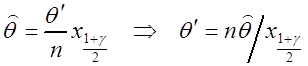 . Доверительный интервал имеет вид
. Доверительный интервал имеет вид
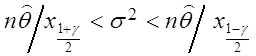 .
.
Пример 3.11. Построить доверительный интервал
доверительной вероятности ![]() для
параметров нормального распределения
для
параметров нормального распределения ![]() ,
, ![]() (оба параметра неизвестны).
(оба параметра неизвестны).
Решение. В качестве оценок неизвестных параметров выбираем ![]() ,
, ![]() (исправленная
выборочная дисперсия), тогда случайная величина
(исправленная
выборочная дисперсия), тогда случайная величина  имеет
распределение Стьюдента с
имеет
распределение Стьюдента с ![]() степенями
свободы (см. подразд. 2.14), т.е.
степенями
свободы (см. подразд. 2.14), т.е.
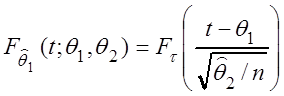 .
.
Далее доверительный интервал для ![]() строится,
как в примере 3.9, и имеет вид
строится,
как в примере 3.9, и имеет вид
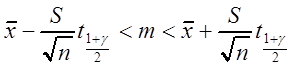 ,
,
только теперь здесь ![]() квантиль
уровня
квантиль
уровня  распределения Стьюдента с
распределения Стьюдента с ![]() степенями свободы. Доверительный
интервал для
степенями свободы. Доверительный
интервал для ![]() строится так же, как в
примере 3.10, но с использованием
строится так же, как в
примере 3.10, но с использованием ![]() -распределения
с
-распределения
с ![]() степенями свободы
степенями свободы
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.