. Для выражения K(JQ) сделаем замену z~x = ej и после группировки членов получим
KQQ) = [Во-Я.(е/0- е-'°) -52(е,2в- е^е) Д^»-е^°)] е
Используя вытекающее из формулы Эйлера соотношение е/0- ет/ = 2/ sin 0, получим
Для обеспечения Re[AXj0)] = 0 необходимо принять у50=0. В этом случае
Очевидно, что идеальный ПГ нереализуем, так как требует бесконечно большого числа элементов задержки.
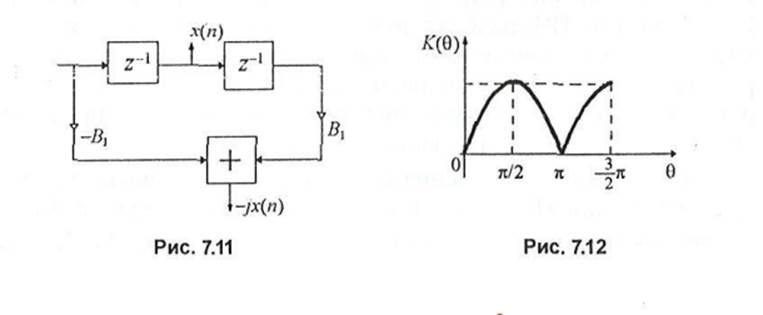
Рассмотрим характеристики ПГ при ограниченном числе элементов задержки. При 2N=2 имеем ЛГ(0) = | 251 sin 0 |. Структурная схема ПГ на двух элементах задержки приведена на рис. 7.11.
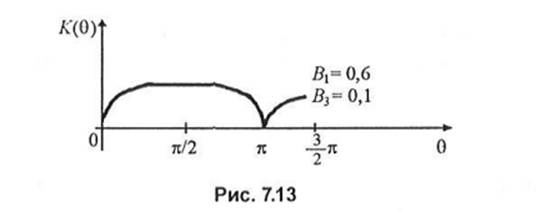
Для получения К(п/2) = 1 коэффициент В\ должен быть равен 0,5. При В = 0,5 АЧХ ПГ на двух элементах задержки приведена на рис. 7.12. Из этого рисунка видно, что в компоненте -jx(ri) возникают амплитудно-частотные искажения.
Разложение функции на рис. 7.9 в ряд Фурье содержит только нечетные гармоники синуса частоты 9, поэтому реальный ПГ с ограниченным числом элементов задержки 2N будет иметь коэффициенты В,„ для четных т, близкие или равные нулю, а для нечетных т — близкие к значениям Вт - 2/пт.
Расчет коэффициентов В„, для ПГ чаще всего выполняется как и для нерекурсивного фильтра одним из трех методов: методом Фурье с применением оконных функций, методом наименьших квадратов и методом, основанным на алгоритме Ремеза.
Для ПГ на шести элементах задержки при В2 = 0
Щ) = \В] sine+Яз sin 30 |.
Близкая к плоской АЧХ в окрестности 0 = тс/2 обеспечивается при коэффициентах Вх = 0,6, В3 = 0,\. На рис. 7.13 приведена АЧХ ПГ на шести элементах задержки.
7.3.3. ЦИФРОВЫЕ ПРЕОБРАЗОВАТЕЛИ ЧАСТОТЫ
Преобразователи частоты (ПЧ) служат для переноса спектра сигнала из одной области частот в другую. В основе работы цифрового ПЧ лежит перемножение выборок сигнала на выборки из гармонического вспомогательного колебания, формируемого цифровым генератором. Построению цифровых генераторов посвящен раздел 7.3.6.
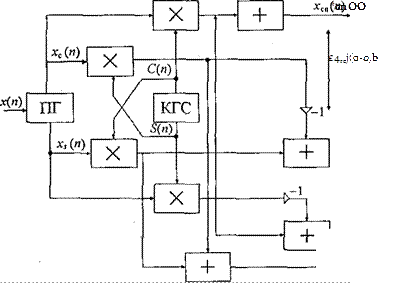
Структурная схема квадратурного ПЧ без побочных продуктов преобразования приведена на рис. 7.14. В ее состав входит ПГ, косинусно-синусный генератор (КСГ), четыре перемножителя, два сумматора и два вычитателя.
На выходах ПГ и КСГ имеем комплексные сигналы Xe'Q" и ArQ±J т". После перемножения и суммирования получим сигнал J£4rc/"(0~0г,", сдвинутый вниз на частоту 0Г= 2nFrTa, а после вычитателя имеем сигнал X/f,e/(0+0l)", сдвинутый вверх на частоту 0Г. Квадратурные ПЧ находят широкое применение в устройствах ЦОС, так как они позволяют обрабатывать сигналы с полосой, определяемой пределом Котельникова П < 0,5/v Кроме того, в квадратурных ПЧ частота гетеродина может изменяться в пределах от -0,5Fa до +0,5/^, включая частоту -Fr-> 0.
Для полного подавления на выходе ПЧ побочных продуктов преобразования ПГ не должен вносить амплитудную и фазовую погрешность в формируемый комплексный сигнал Хс'°", а КГС
 |
должен формировать абсолютно точные квадратурные компоненты С(п) и S(n). Однако реальные нерекурсивные ПГ вносят амплитудные погрешности, а рекурсивные ПГ - фазовые погрешности, поэтому подавление побочных продуктов происходит не полностью.
7.3.4. БЛОКИ ИЗВЛЕЧЕНИЯ КВАДРАТНОГО КОРНЯ
В ряде устройств цифровой обработки сигналов, например, в амплитудных детекторах, необходимо выполнить операциюy=-J~A. В универсальных ЭВМ чаще всего для этих целей применяют итерационную формулу Герона
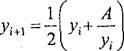
ГДС УьУг+х — результаты вычисления на /-ом и i + 1-ом шагах итерации. В качестве начального приближения обычно принимают
Уо = Л,
Пример. А = 0,85. Из формулы Герона при>"о= 0,85 получим у\ = 0,925; ^2 = 0,92195945; у3 = 0,92195445. Точное значение Jojiti^ 0,92195444.
Как видно из примера, уже на третьем шаге итерации формула Герона дает практически точный результат. Однако в ней есть операция деления, реализация которой затруднительна в процессорах цифровой обработки сигналов.
Для диапазона значений С<А<\ можно воспользоваться другой итерационной формулой. Для этого выражение -JA должно быть представлено в виде -j~A = -Ja + b. Тогда
Ум =У1+^(Л~у!)-Нулевое приближение^ определяется из формул Понселе
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.