Наиболее часто используемый метод численного интегрирования дифференциальных уравнений – метод Рунге-Кутта четвертого порядка.
Пусть дана система дифференциальных уравнений, начальные условия y(x0)=y0.
Зададимся некоторым шагом h и введем обозначение Dyi=yi+1-yi. DYi – приращение, которое определяется суммой четырех приращений, взятых с различными коофициентами:
k1=h*f(xi,yi)
k2=h*f(xi+h/2,yi+k1/2)
k3=h*f(xi+h/2,yi+k2/2)
k4=h*f(xi+h,yi+k3)
Согласно методу Рунге-Кутта Dy0 приближенно определяют по формуле
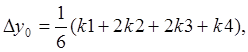 отсюда y1=y0+Dy0.
отсюда y1=y0+Dy0.
Далее, приняв (x1,y1) за исходные данные и повторяя тот же процесс, находим y2. Аналогично вычисляются yi (i=3, 4,…).
Правило рунге:
Метод рунге-кутта требует гораздо больше вычислений, чем какие-либо другие методы, однако это компенсируется значительным увеличением его точности.
Это позволяет значительно увеличивать шаг интегрирования h. Этот шаг должен быть выбран таким, чтобы он был существенно меньше интервала, на котором решение диф. уравнения значительно меняется. В противном случае погрешность будет очень велика. Удобный практический способ оценки погрешности и правильного выбора шага h даёт правило рунге.
Пусть решение у(xi) в точке xi найдено. Найдено решение у(xi+h) двумя способами: сначала сделав шаг величиной h, а затем два шага по h/2. Обозначим эти решения как yh и yh2. Тогда по правилу рунге погрешности решения R для метода р-ого порядка точности равняются:ААА
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.