3 ЭЛЕМЕНТЫ ТЕОРИИ ГРАФОВ
3.1 Основные определения
Граф G(V,E)– совокупность двух множеств V и E, причем множество вершин V=![]() непустое,
а множество E=
непустое,
а множество E=![]() представляет собою набор неупорядоченных или упорядоченных пар вершин,
то есть
представляет собою набор неупорядоченных или упорядоченных пар вершин,
то есть ![]() . Множество Е принято называть
множеством ребер или дуг. Количество вершин и ребер можно обозначить n(G) и m(G) соответственно.
. Множество Е принято называть
множеством ребер или дуг. Количество вершин и ребер можно обозначить n(G) и m(G) соответственно.
Граф, в
котором множество E=![]() представляет собою
набор неупорядоченных пар вершин, называют неориентированным.
представляет собою
набор неупорядоченных пар вершин, называют неориентированным.
Граф, в
котором множество E=![]() представляет собою
набор упорядоченных пар вершин, называют ориентированным или орграфом. В орграфе для каждого ребра
определены его начало ( первый элемент в паре вершин) и конец (второй элемент в
паре вершин).
представляет собою
набор упорядоченных пар вершин, называют ориентированным или орграфом. В орграфе для каждого ребра
определены его начало ( первый элемент в паре вершин) и конец (второй элемент в
паре вершин).
Пара вершин может быть соединена несколькими ребрами. Такие ребра в графе называют кратными. Ребро может соединять вершину саму с собою, и такое ребро называют петлей. Вершины, соединенные ребром , называют смежными вершинами. Ребра, имеющие общую вершину, тоже называют смежными.
Ребро инцидентно вершине, если эта вершина является одним из его концов.
Граф без кратных ребер и петель называется простым графом.
Простой граф, любые две вершины которого являются смежными, называется полным.
Подграфом графа G(V,E) называется граф, все вершины и ребра которого содержатся среди вершин и ребер исходного графа.
Степенью вершины ![]() неориентированного графа называется
количество ребер
неориентированного графа называется
количество ребер ![]() , инцидентных вершине.
При этом петли учитываются дважды. Вершину со степенью ноль называют
изолированной.
, инцидентных вершине.
При этом петли учитываются дважды. Вершину со степенью ноль называют
изолированной.
Полустепенью исхода (захода ) вершины ![]() орграфа называется количество ребер
орграфа называется количество ребер ![]() , исходящих из вершины
( заходящих в вершину
, исходящих из вершины
( заходящих в вершину ![]() ). Петля,
инцидентная вершине, учитывается как в
). Петля,
инцидентная вершине, учитывается как в ![]() ,
так и в
,
так и в ![]() .
.
Теорема.
Для
неориентированного графа ![]() .
.
Для
орграфа ![]() .
.
Маршрутом в графе G(V,E)
называется последовательность вершин и ребер ![]() ,
причем любые соседние вершина и ребро
,
причем любые соседние вершина и ребро ![]() в
этой последовательности инцидентны. Путь
( ориентированный маршрут ) представляет собою
последовательность вершин и ребер
в
этой последовательности инцидентны. Путь
( ориентированный маршрут ) представляет собою
последовательность вершин и ребер ![]() , где каждое
ребро
, где каждое
ребро ![]() является парой упорядоченных вершин
является парой упорядоченных вершин ![]() . Маршрут, в котором все ребра
попарно различны, называется простым
маршрутом.
. Маршрут, в котором все ребра
попарно различны, называется простым
маршрутом.
Замкнутый маршрут, в котором все ребра попарно различны, называется циклом. Замкнутый путь, в котором все ребра попарно различны, называется контуром. Цикл ( контур ), в котором все вершины попарно различны, называется простым циклом ( контуром ).
Два графа G(V,E) и G1(V1,E1) называются изоморфными, если существует взаимно - однозначное соответствие между множествами вершин V,V1 и множествами ребер E,E1 , сохраняющее инцидентность. Изоморфизм можно определить иначе – граф G можно так перерисовать ( расположив его вершины и ребра по – другому ), что получится граф G1 .
Рисунки 3.1 и 3.2 иллюстрируют приведенные выше понятия.
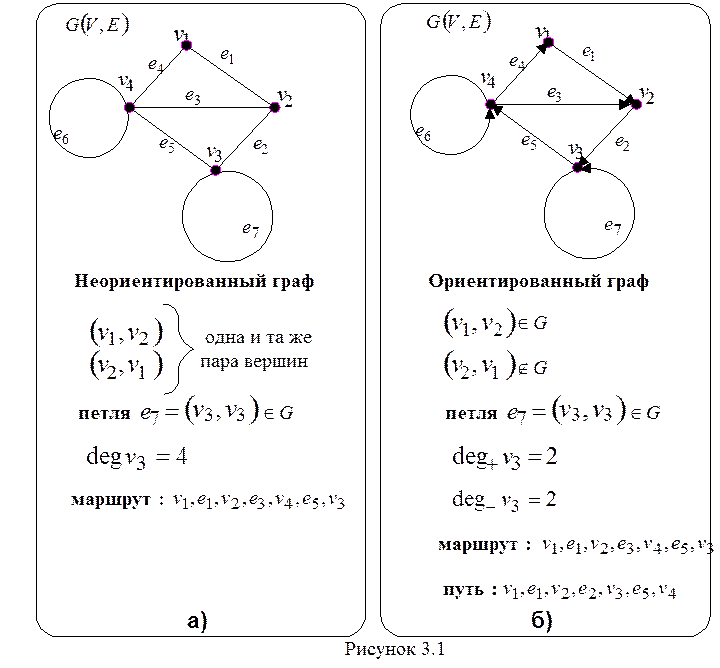
 Неориентированный граф G(V,E) называется связным,
если в нем существует маршрут между каждой парой вершин. Например, граф на
рисунке 3.1 а) - связный. Ориентированный граф называется связным, если
связным является лежащий в его основе неориентированный граф.
Неориентированный граф G(V,E) называется связным,
если в нем существует маршрут между каждой парой вершин. Например, граф на
рисунке 3.1 а) - связный. Ориентированный граф называется связным, если
связным является лежащий в его основе неориентированный граф.
Связный граф без циклов называется деревом. В дереве между любыми двумя вершинами существует только один простой маршрут. Количество ребер в дереве на единицу меньше, чем количество вершин. Если соединить ребром произвольные две несмежные вершины дерева, то получается граф, имеющий только один цикл.
3.2 Матрица инциденций орграфа
Пусть имеется граф G(V,E) без
петель на n вершинах и m ребрах. Матрица инциденций ![]() графа G
имеет n строк (по одной на
каждую вершину) и m столбцов (по одному
на каждое ребро). Элемент
графа G
имеет n строк (по одной на
каждую вершину) и m столбцов (по одному
на каждое ребро). Элемент ![]() матрицы
матрицы ![]() определяется следующим образом:
определяется следующим образом:
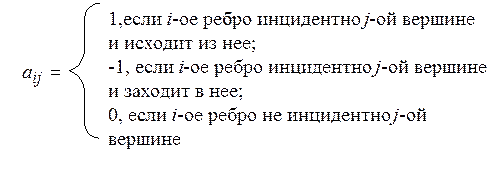
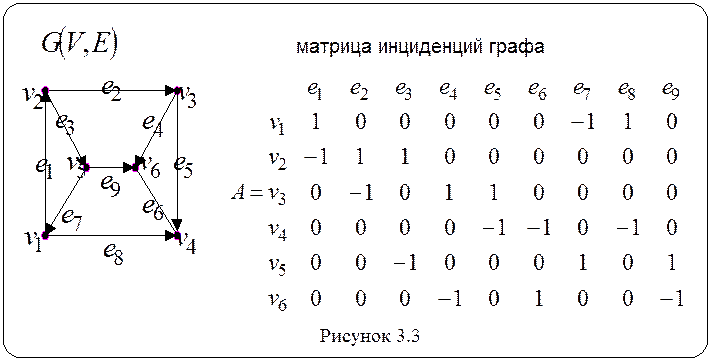 На рисунке 3.3 приведен пример
графа и его матрицы инциденций.
На рисунке 3.3 приведен пример
графа и его матрицы инциденций.
Из определения следует, что сумма элементов каждого столбца матрицы инциденций равна нулю.
3.3 Фундаментальные разрезы и фундаментальные циклы графа
Связный ациклический подграф графа G на всех вершинах называют остовом графа G. Ребра остова называют ветвями, а остальные ребра графа G, на входящие в остов, называют хордами.
Если усечь матрицу инциденций графа по какой – либо строке, то можно вычислить количество остовов и выделить каждый остов графа.
Количество
остовов равно ![]() . Каждому ненулевому минору
усеченной матрицы инциденций порядка n-1 ( n – количество вершин графа) соответствует остов. Ветви остова
соответствуют столбцам такого минора. Рисунок 3.4 иллюстрирует последние
утверждения.
. Каждому ненулевому минору
усеченной матрицы инциденций порядка n-1 ( n – количество вершин графа) соответствует остов. Ветви остова
соответствуют столбцам такого минора. Рисунок 3.4 иллюстрирует последние
утверждения.
Если из остова T графа G удалить одну ветвь ek, то множество его вершин V разбивается на два не связанных между собой подмножества W1 и W2 . Все ребра графа G, имеющие один конец в W1, а другой конец в W2, составляют фундаментальный разрез для остова T. Направление разреза выбирают по направлению породившей его ветви. Количество фундаментальных разрезов равно количеству ветвей.
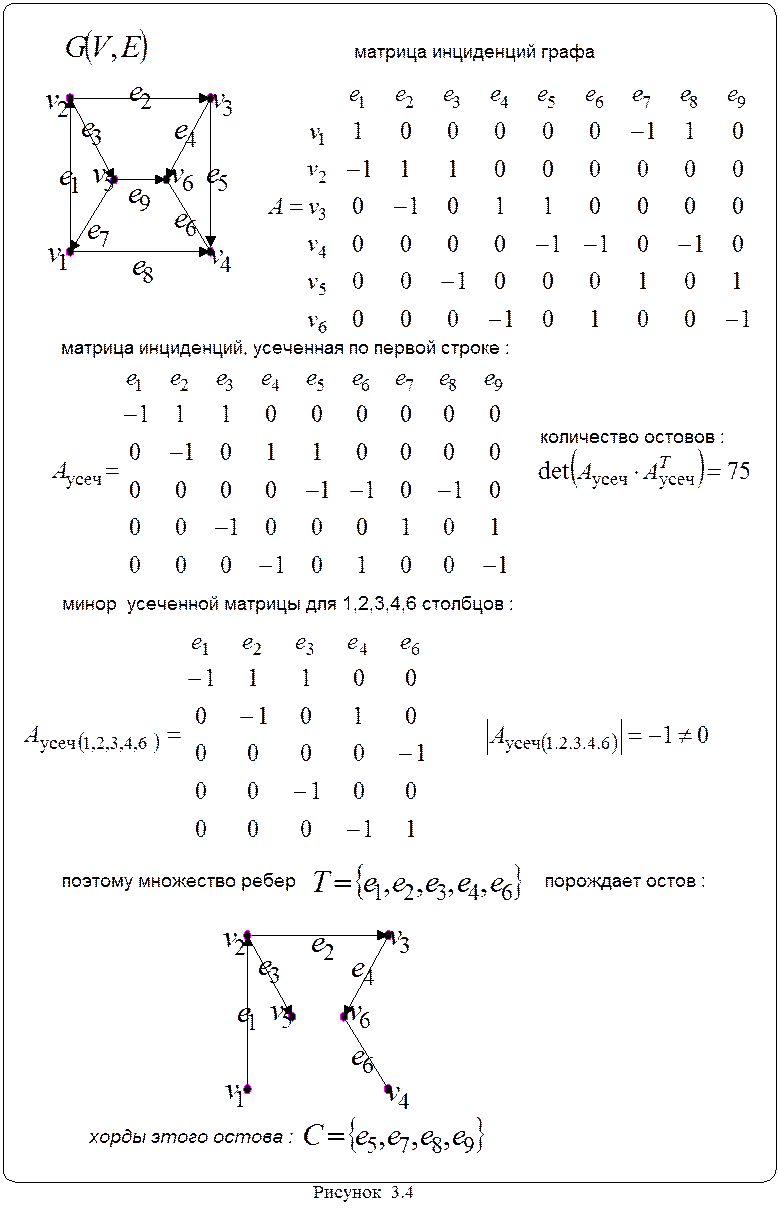
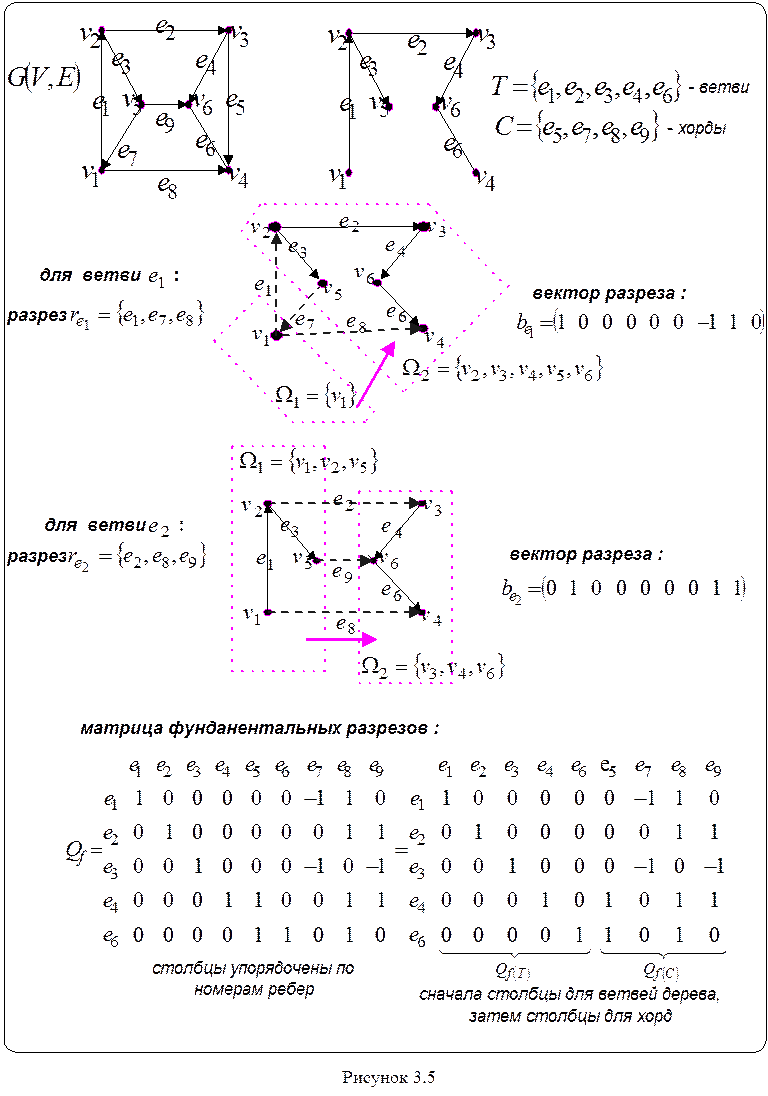
Каждому фундаментальному разрезу можно поставить в соответствие вектор - строку, элементы которого определяются по правилу:
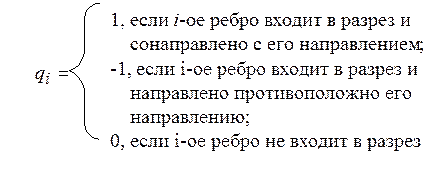
Из таких
векторов - строк составляется матрица фундаментальных разрезов![]() . Количество строк в ней совпадает с
количеством ветвей остова, а количество столбцов равно количеству столбцов
исходного графа G. Процесс составления матрицы
фундаментальных разрезов показан на рисунке 3.5 .
. Количество строк в ней совпадает с
количеством ветвей остова, а количество столбцов равно количеству столбцов
исходного графа G. Процесс составления матрицы
фундаментальных разрезов показан на рисунке 3.5 .
Если к остову T графа G добавить одну хорду ek, то в результате образуется только один цикл. Множество ребер, входящих в полученный цикл, составляет фундаментальный цикл графа G для остова T . Направление обхода цикла выбирается по направлению породившей этот цикл хорды. Каждому фундаментальному циклу можно поставить в соответствие вектор - строку, элементы которого определяются по правилу:
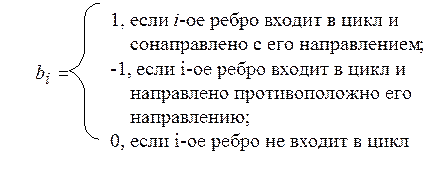
Из таких
векторов - строк составляется матрица фундаментальных циклов![]() . Количество строк в ней совпадает с
количеством хорд остова, а количество столбцов равно количеству столбцов
исходного графа G. Процесс составления матрицы
фундаментальных циклов показан на рисунке 3.6 .
. Количество строк в ней совпадает с
количеством хорд остова, а количество столбцов равно количеству столбцов
исходного графа G. Процесс составления матрицы
фундаментальных циклов показан на рисунке 3.6 .
В матрицах
фундаментальных разрезов![]() и фундаментальных
циклов
и фундаментальных
циклов![]() можно выделить столбцы, соответствующие
ветвям (
можно выделить столбцы, соответствующие
ветвям (![]() ,
,![]() )
и хордам (
)
и хордам (![]() ,
,![]() )
остова. Матрицы связаны между собой соотношением :
)
остова. Матрицы связаны между собой соотношением :
![]() .
.
Этот факт проиллюстрирован на рисунке 3.7 .
Матрицы инциденций, фундаментальных разрезов, фундаментальных циклов используются при исследовании электрических цепей. Эти матрицы входят в качестве коэффициентов в уравнения Кирхгофа, описывающие цепь.
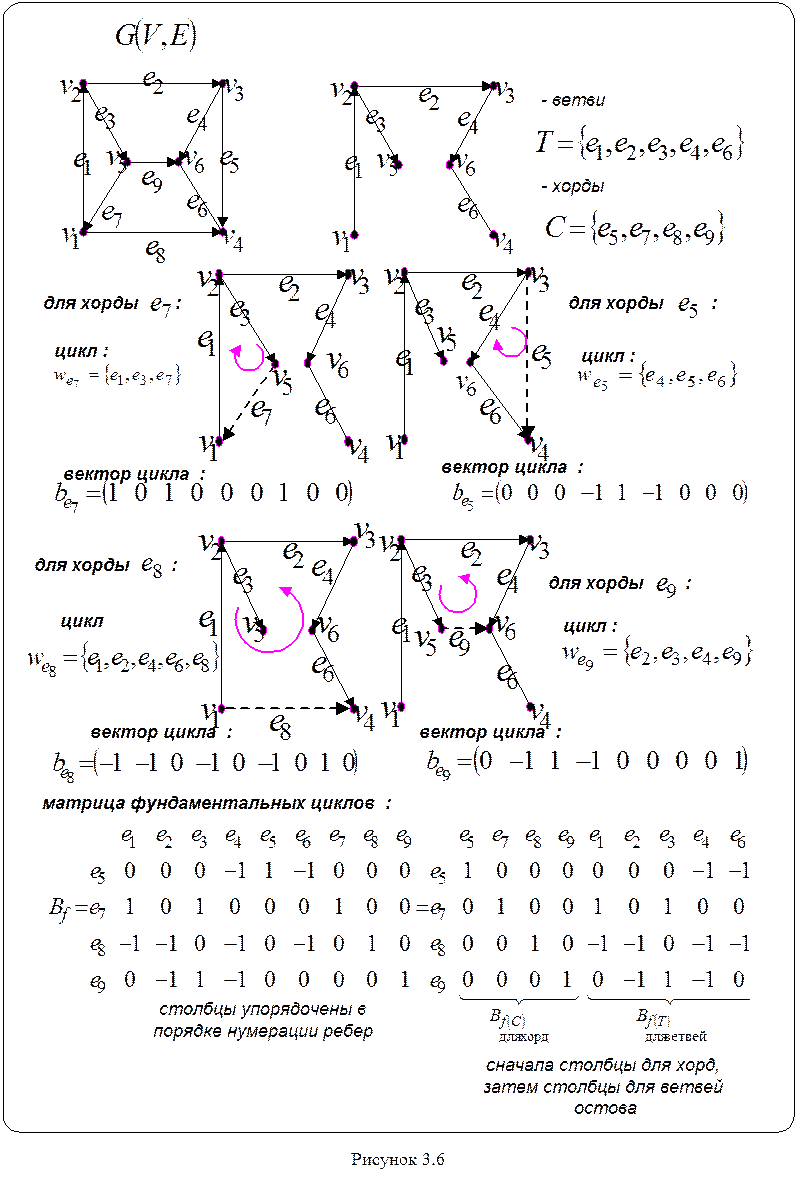
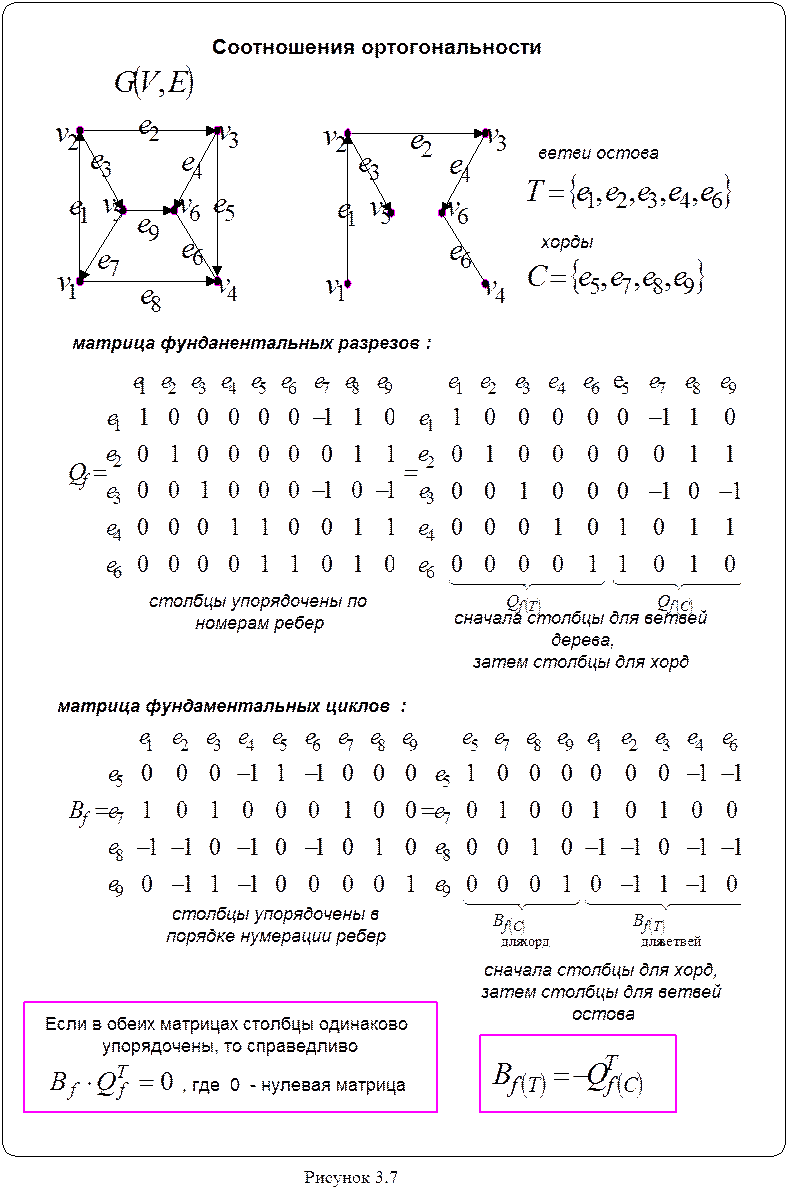
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.