Понятие матрицы. Действия над матрицами. Свойства алгебраического дополнения. Система линейных алгебраических уравнений

ПОНЯТИЕ МАТРИЦЫ. ДЕЙСТВИЯ НАД МАТРИЦАМИ

Матрица – прямоугольная таблица чисел, состоящая из m сток и

n столбцов.

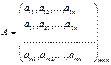где

Размерностью матрицы называется кол-во строк и столбцов

Если количество строк равно количеству столбцов, то матрица называется квадратной. Если i=1, j>1, то матрица называется

вектор-строкой. Если i>1, j=1, то матрица называется

вектор-столбец.

Свойства матрицы:

1) суммой 2х матриц с одинаковым кол-вом строк и столбцов называется матрица, элементы которой получены сложением одноименных элементов.

2) произведением матрицы на число называется матрица, у которой каждый элемент равен произведению соответствующего элемента матрицы на это число.

3) произведением 2х матриц называется матрица, которая получается умножением элементов i-ой строки 1го множителя на элементы j-ого столбца 2го множителя и полученные элементы сложить.

Треугольная матрица – квадратная матрица, в которой выше или ниже главной диагонали стоят нули. Диагональная матрица – это матрица, в которой элементы главной диагонали не равны нулю, все остальные нули. Единичная матрица – матрица, по главной диагонали, которой стоят единицы, все остальные нули.

Транспонированием матрицы называется замена строк столбцами.

ОПРЕДЕЛИТЕЛИ 2го ПОРЯДКА (ΔΙΙ)

Свойства:

1) определитель не изменится, если его строки поменять местами соответствующими столбцами.

2) при перестановке 2х строк (столбцов) определитель изменит знак на противоположный сохраняя абсолютную величину.

3) определитель с 2мя одинаковыми столбцами

(строками) равен нулю.

4) общий множитель всех элементов строки (столбца)

можно выносить за знак определителя.

5) если элементы какой-либо строки (столбца) равен нулю, то определитель равен нулю.

6) если к элементам какой-либо строки (столбца)

прибавить соответствующие элементы другой строки

(столбца), умноженные на одно и тоже число, то определитель не изменит своей величины.

ОПРЕДЕЛИТЕЛИ 3го ПОРЯДКА (ΔΙΙΙ)

ΔΙΙΙ – число, полученное разложением ΔΙΙΙ

по элементам 1й строки и сводится к вычислению ΔΙΙ.

Вычисление определителя по правилу Δ-ка:

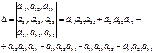
Минором соответствующим элементам ΔΙΙΙ

называется ΔΙΙ, полученный из данного вычеркиванием строки и столбца на пересечении которых стоит данный элемент

Δ = a₁₁M₁₁ - a₁₂M₁₂ + a₁₃M₁₃

Алгебраическое дополнение – минор, взятый со знаком “+”, если сумма номеров строки и столбца где стоит элемент четная, и со знаком

“-”, если эта сумма нечетная.

A_ij = (-1)^i+j ∙ M_ij

Δ = a₁₁A₁₁ - a₁₂A₁₂ + a₁₃A₁₃

Свойства алгебраического дополнения: сумма произведений элементов какой-либо строки

(столбца) определителя на алгебраические дополнения соответствующих элементов другой строки (столбца) равна нулю.

МАТРИЧНЫЙ СПОСОБ

Применяется, если число уравнений совпадает с числом неизвестных и главный определитель не равен нулю.

Х=А^-1∙В

А_ij – алгебраические дополнения

ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ

Векторным произведением векторов a и b

называется такой вектор с, который определяется:

а) |c| численно равен площади параллелограмма построенного на перемножаемых векторах a и b

как на сторонах, т.е. |c|=|a|∙|b|sinφ.

б) вектор с ортогонален обоим множителям в) направление вектора с таковó, что если смотреть из его конца вдоль вектора, то поворот от вектора а

до b виден против часовой стрелки.

Угол между вектором с и плоскостью, образованной векторами а и b называется:

Свойства:

1) при перестановке сомножителей векторное произведение меняет свой знак сохраняя модуль:

2) векторное произведение обладает сочетательным свойством относительно скалярного множителя:

3) векторное произвед-е обладает распред-м св-вом:

4) если векторное произведение 2х векторов =0, то либо равен нуль-вектору один из множителей, либо равен нулю sin угла м/у ними:

5)

СИСТЕМА ЛИНЕЙНЫХ

АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ

СЛАУ – система линейных алгебраических уравнений называется система

х₁, х₂, х₃ – неизвестные

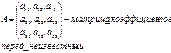
Тройка (х₁, х₂, х₃) называется решением СЛАУ

если в результате подстановки их значений вместо неизвестных в уравнение системы каждое уравнение обращается в верное тождество.

Главным определителем СЛАУ называется определитель матрицы А:

Система уравнений из 3х линейных уравнений с

3мя неизвестными называется совместной, если главный определитель не равен нулю. Если определитель существует и отличен от нуля, то существует единственное решение СЛАУ и оно может быть найдено через формулы Крамера, матричным способом и методом Гаусса. СЛАУ

называется однородной, если столбец свободных членов равен нулю. Ранг однородной системы получается из матрицы добавлением нулевого столбца и их ранги совпадают: если ранг матрицы равен количеству неизвестных, то система имеет единственное решение; если ранг матрицы меньше количества неизвестных, то система имеет множество решений

ФОРМУЛЫ КРАМЕРА

     

Δх₁, Δх₂, Δх₃ – второстепенные определители

Чтобы найти второстепенный определитель

Δх₁ необходимо в главном определителе

1й столбец заменить столбцом свободных членов

Второстепенный определитель Δх₂ находится из главного определителя заменой 2го столбца столбцом свободных членов

    

Способ применим, если количество уравнений совпадает с количеством неизвестных.

ОБРАТНАЯ МАТРИЦА

Обратной матрицей называется

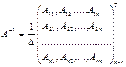
А_ij – алгебраические дополнения

Свойства обратной матрицы: произведение матрицы на обратную матрицу равно единичной матрицы А∙А^-1=А^-1∙А=Е

       

ПАРАБОЛА

Параболой называется множество всех точек плоскости, каждая из которых одинаково удалена от данной точки, называемой фокусом, и данной прямой, называемой директрисой. Расстояние от фокуса F до директрисы называются параметром параболы р (р>0).  Пусть

М(х;у) – произвольная точка параболы. По определению параболы MF = MN.

 

Возведя обе части уравнения в квадрат, получим:

у² = 2рх – каноническое уравнение параболы.

Уравнения у² = -2рх (ветки направлены влево), х² = 2ру (ввеарх), х² = -2ру (вниз) (p > 0) также определяют параболу.

МЕТОД ГАУССА

Рангом матрицы называется наибольший порядок, получаемый из матрицы ненулевых миноров. Если миноры ΔΙΙΙ = 0, то ранг матрицы не равен 3м. Элементарными

преобразованиями над ‌‌|| рядами матрицы называется: смена местами рядов; умножение ряда на число; умножение ряда на число и сложение с другим рядом. Элементарные преобразованиями над ‌‌|| рядами матрицы не изменяют его ранга. Элементарные преобразования позволяют преобразовать матрицу к треугольному виду. Если матричный метод или метод Крамера не применим (Δ = 0), то применяют метод Гаусса: приведение матрицы к треугольному виду с помощью элементарных преобразований.

ВЕКТОРЫ

Вектором называется направленный отрезок прямой. Длиной вектора называется длина его отрезка. Если длина вектора равна 1, то вектор называется единичным . Если длина вектора равна 0, то вектор называется

нулевым . Векторы называются

коллинеарными, если они лежат на ||-х прямых.

Два вектора называются равными, если их длины равны и они сонаправлены. Три вектора называются компланарными, если они лежат на одной плоскости или в ||-х плоскостях. Тройка некомпланарных векторов называется правой, если смотря из конца 3го вектора кратчайший поворот от 1го вектора ко 2му будет виден как движение против часовой стрелки. Если правило не выполняется, то тройка левая. Сложение векторов: с=а+в (из начала 1го в конец 2го). Разность: с=а+в=а+(-в)

(из начала 1го в конец 2го). Произведением

вектора ā на число λ называется вектор с

коллинеарный ā, имеющий длину .

       

ПРОЕКЦИЯ ВЕКТОРА

Проекцией вектора АВ на ось l называется произведение длины вектора АВ на cos угла между АВ и осью l.

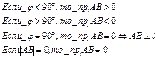
Свойства проекций: 1) проекция суммы 2х векторов на ось равна сумме проекций слагаемых векторов на туже ось.

2) проекция вектора на ось равна разности координат проекций конца и начала вектора.

пр_lā=x₂-x₁

3)если вектор умножить на число, то его проекция на ось также умножается на число пр_l(k∙ā)=k∙пр_lā

Векторы называются ортогональными, если они перпендикулярные.

Свойства векторов:

1) коммутативность a+b=b+a

2) дистрибутивность λ(a+b)=λa+λb, λ - число

3) дистрибутивность относительно умножения на вектор (α+β)ā=αā+βā, где α, β – const, т.е. числа.

СИСТЕМА ДЕКАРТОВЫХ ПРЯМОУГОЛЬНЫХ

КООРДИНАТ В ПРОСТРАНСТВЕ

Координатами вектора в декартовой прямоугольной системе координат называется проекцией этого вектора на оси координат.

1) в плоскости. пр_охā = х-0 = х; пр_оуā = у-0 = у; ā={х;у}=

={ пр_охā; пр_оуā}

2) в пространстве. х = пр_охā, у = пр_оуā, z = пр_оzā,

ā={x; y; z}.

Ортами называются единичные отрезки, лежащие на осях координат. iє ox, |i|=1; j є oy, |j|=1; k є oz, |k|=1.

ox┴oy┴oz => i┴j┴k. Т.к. орты ортогональны, некомпланарны, то они образуют базис, который называется декартовым ортогональным базисом.

Разложение вектора на составляющие по координатным осям: ā=x∙i+y∙j+z∙k. Модулем (длиной) вектора

называется корень квадратный из суммы квадратов его проекций на оси координат.. Если вектор задан координатами начала и конца вектора АВ:

А(х₁,у₁,z₁), В(x₂,y₂,z₂), то пр_охАВ = х₂ – х₁, пр_оуАВ = у₂ – у₁, пр_оzАВ = z₂ – z₁,

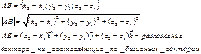
ЛИНЕЙНЫЕ КОМБИНАЦИИ ВЕКТОРОВ

А(х_а; у_а; z_a), М(х_м; у_м; z_м), В(х_в; у_в; z_в)

АМ={x_м - х_а; у_м - у_а}, АВ={x_в - х_а; у_в - у_а},

МВ={x_в – х_м; у_в – у_м}

Линейной комбинацией n векторов (ā₁,ā₂…ā_n)

называется сумма произведений:

Векторы называются линейно зависимыми, если их комбинация равна нулю при ненулевых коэф-х λ.

Векторы называются линейно независимыми, если их линейная комбинация равна нулю только при ненулевых коэф-х.

Теор: любые 2 коллин-х вектора линейно зависимые.

Теор: любые 3 комплан-х вектора линейно зависимые.

Теор: любой вектор пространства можно представить в виде линейной комбинации 3х линейно независимых векторов и эта комбинация единственная.

НАПРАВЛЯЮЩИЕ COS ВЕКТОРА

Направление вектора в пространстве определяется углами, который вектор составляет с осями. Cos этих углов называются направляющие cos этого вектора.

α = ā;ох   β = ā;оу   γ = ā;oz

cos²α+cos²β+cos²γ=1

 

СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ

Скалярным произведением векторов а и b называется число, равное произведению модулей перемножаемых векторов на cos угла между ними

Скалярным произведением 2х векторов называется число, полученное произведением модуля одного из векторов на проекцию на него другого вектора

Свойства:

1) коммутативность: скалярное произведение 2х векторов не изменится, если множители поменять местами: a∙b=b∙a

2) скалярное произведение 2х векторов обладает сочетательным свойством относительно скалярного множителя: λ(a∙b)=(λ∙a)b=a(λ∙b)

3) скалярное произведение 2х векторов обладает распределительным свойством: (a+b)c=ac+bc

4) если скалярное произведение 2х векторов равно нулю

, то равен нулю либо один из перемножаемых векторов, либо cos угла между ними. Если cos угла между ними равен 0, то векторы ортогональны: a∙b=0<=>a┴b

5) скалярный квадрат вектора равен квадрату его модуля: ā²=|ā|²

6) для того, чтобы векторы были ортогональны необходимо и достаточно, что сумма парных произведений их одноименных координат (проекций)

равнялась нулю: a∙b=0óx₁x₂+y₁y₂+z₁z₂=0

ПРЯМАЯ И ПЛОСКОСТЬ

В ПРОСТРАНСТВЕ

Пусть плоскость Q задана уравнением Ах + Ву + Cz + D = 0, а прямая L уравнениями

Угол между прямой и плоскостью называется любой из двух смежных углов, образованных прямой и ее проекцией на плоскости. φ – угол между плоскостью Q и прямой L, θ – угол между нормальным вектором и направляющим вектором S

прямой L. Тогда . Найдем sinφ, считая φ≤π/2:

sinφ = sin(π/2 - θ) = cosθ. Т.к. sinφ ≥ 0 получаем

Если прямая L параллельна плоскости Q, то векторы N и S ┴ и

N∙ S = 0, т.е. Am + Bn + Cp = 0 – условие параллельности прямой и плоскости. Если прямая перпендикулярна плоскости, то векторы N и S параллельны. Поэтому равенства A/m=B/n=C/p

являются условиями перпендикулярности прямой и плоскости.

СМЕШАННОЕ ПРОИЗВЕДДЕНИЕ ВЕКТОРОВ

Смешанным произведение 3х векторов называется векторное произведение скалярно умноженное на

3й вектор: (a×b)∙c=(abc). Пусть векторы заданы своими линейным разложениями в базисе:

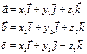
Смешанное произведение в координатной форме равно определителю 3го порядка, составленного из координат этого вектора:

Свойства:

1) при перестановке множителей результат меняет знак:

2) смешанное произведение 3х векторов с точностью до знака равна объему парал-да, построенного на этих векторах как на ребрах:

3) если смешанное произведение равно отрицательному значению, то тройка векторов

abc левая.

4) для того, чтобы векторы abc были компланарны необходимо и достаточно, чтобы их смешанное произведение равнялось нулю.

 

ПОЛЯРНЫЕ КООРИНАТЫ

Пусть задана на плоскости числовая ось, называемая полярной осью. Ее начало называется полюсом. Пусть задана произвольная точка М. Пусть угол между полярной осью и прямой, на которой лежит точка М называется полярным углом φ. Расстояние от полюса до точки называется полярным радиусом r. Тогда точка в полярной системе координат задается полярным углом и полярным радиусом. M(φ;r)

ЗАВИСИМОСТЬ ДЕКАРТОВЫХ И

ПОЛЯРНЫХ КООРДИНАТ

Пусть х и у -  прямоугольные координаты точки М, а r и φ – ее полярные координаты.

cosφ = x/r  sinφ = y/r  x = r∙cosφ  y = r∙sinφ

cos²φ+sin²φ=x²/r²+y²/r²=(x²+y²)/r²

1=(x²+y²)/r² => x²+y²=r²

составим отношение декартовых корд у/х

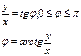
РАССТОЯНИЕ МЕЖДУ

2мя ТОЧКАМИ

Задана прямоугольная система координат в пространстве

М₁М₂ – диагональ

M₁F; M₁P; M₁Q – измерения

М₁М₂² = M₁F² + M₁P² + M₁Q²

Построим проекции измерений на оси:

M₁Р = пр_охМ₁М₂ = |x₂ – x₁| > 0

M₁F = пр_оyМ₁М₂ = |y₂ – y₁| > 0

M₁Q = пр_оzМ₁М₂ = |z₂ – z₁| > 0

M₁M₂=d

d² = |x₂ - x₁|² +|y₂ - y₁|² +|z₂ - z₁|²

d² = (x₂ - x₁)² +(y₂ - y₁)² +(z₂ - z₁)²

Формула справедлива, если М₁М₂ ||

хотя бы одной из осей. Если

М₁ = 0 (0;0;0), тогда

     

ПРЯМАЯ НА ПЛОСКОСТИ.

УРАВНЕНИЯ ПРЯМОЙ НА ПЛОСКОСТИ

Пусть задана функция y=f(x). Линия, являющаяся графиком этой ф-ии состоит из точек плоскости, удовлетворяющих уравнению y=f(x). Если М(х;у)

принадлежит указанной линии, то ее координаты удовлетворяют уравнению линии.

1) Пусть задана прямая l плоскости ХОУ. М1єl и является подвижной. Пусть М(х;у)єl и является неподвижной. Рассмотрим вектор N, ┴й l. Этот вектор называется нормальный вектор.

N={A;B}.N┴l; MM₁єl => N┴MM₁ =>N∙MM₁=0.

Пусть ММ₁ || М₁М = {x-x₁;y-y₁;z-z₁}=>N∙M₁M=0 =>

A(x - x₁) + B(y - y₁) + C(z - z₁) = 0 – уравнение прямой, проходящей через М₁(х₁;у₁;z₁)┴N(A;B) в пространстве.

2) Пусть задано уравнение прямой, проходящей через данную точку ┴ данному вектору

А(х - х₁) + В(у - у₁) = 0

Ах - Ах₁ + Ву - Ву₁ = 0

Ах + Ву + (-Ах₁ – Ву₁) = 0

Ах + Ву + С = 0 – общее уравнение прямой на плоскости (С - свободный член; А,В – координаты нормального вектора)

3) Рассм вектор || l и нележащий не этой прямой.

S= mi+ nj. S = {m; n}-направляющий вектор прямой S|| l; M₁Mєl => S|| M₁M => их корд пропорциональны

M₁M = {x – x₁; y – y₁; z – z₁}.

4) Пусть вектор M₁M₂ является направляющим вектором прямой

М₁М₂ = {x₂ – x₁; y₂ – y₁}

M₁M || M₁M₂ =>

уравнение прямой, проходящей через 2 точки М₁ и М₂.

5) Если l || OУ, то S={0;r}, то каноническое уравнение прямой будет иметь вид:

S || OX, S = {m; 0}:

         

УРАВНЕНИЕ ПРЯМОЙ С УГЛОВЫМ КОЭФФИЦИЕНТОМ

6) ∆BMK: tgα = MK/BK = (y - b)/k. tgα = k. k = (y - b)/x. y – b = kx.

k – угловой коэффициент прямой. y = kx + b.

b – свободный член. k>0 => прямая лежит в 1 и 3 четверти, угол α

острый. k<0 => прямая во 2 и 4 четверти, угол α тупой.

b равен отрезку, отсекаемый прямой по оси У. Если b=0, то y = kx

это биссектриса, проходящая через начало отсчета. Если k=0, то прямая имеет вид y=b и || оси OX.

7) Расположение прямых на плоскости:

а) Пусть прямые заданы общими уравнениями

l₁: A₁x + B₁y + C₁ = 0      N₁ = {A₁; B₁}

l₂: A₂x + B₂y + C₂ = 0      N₂ = {A₂; B₂}

б) Пусть прямые заданы уравнениями с угловыми коэф

l₁: y = k₁x + b₁

l₂: y = k₂x + b₂

M = l₁ ∩ l₂

tgα₁ = k₁; tgα₂ = k₂

в) Пусть прямые ||

l₁ || l₂ => tgα₁ = tgα₂ <=> k₁ = k₂. N₁ || N₂ => A₁/A₂ = B₁/B₂ – условие параллельности 2х прямых.

г) Пусть прямые ортогональны.

l₁ ┴ l₂ => N₁ ┴ N₂ => N₁∙N₂ = 0, A₁A₂ + B₁B₂ = 0

, l₁ ┴ l₂ => φ = 90° => tg90° = ∞

ctgφ = 1/tgφ = 1/∞ = 0

  

 

8) Уравнение прямой в отрезках. Пусть задано общее уравнение прямой Ах + Ву + С = 0

Числа a и b – величины отрезков, отсекаемые прямой на осях координат.

9) Расстояние от точки до прямой.

l: Ax + By + C = 0   М(х;у)  

Расстоянием от точки до прямой называется перпендикуляр, опущенный из точки на прямую.

N = {A;B}

   

ПЛОСКОСТЬ

1) N┴α  N = {Ai + Bj + Ck}

N = {A;B;C}. Рассмотрим некоторые точки є α.

М₁(x₁;y₁;z₁) M(x;y;z)

M₁M = {x – x₁;y – y₁;z - z₁}

M₁Mєα; N┴α => M₁M┴N => M₁M∙N =0

A(x – x₁) + B(y – y₁) + C(z – z₁) = 0 – уравнение плоскости, проходящей через точку М ┴

нормальному вектору.

2) A(x – x₁) + B(y – y₁) + C(z – z₁) = 0

Ax – Аx₁ + By – Вy₁ + Cz – Сz₁ = 0

Ax + By + Cz + (-Ax₁ - By₁ - Cz₁) = 0

Ax + By + Cz + D = 0 – общее ур-е плоскости.

Если D=0, то Ax + By + Cz = 0 – уравнение плоскости, проходящей через начало координат

3) Ax + By + Cz + D = 0

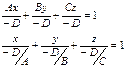
a,b,c – отрезки, отсекаемые плоскостью по осям

4) Даны плоскости общему уравнению

α₁: A₁x + B₁y + C₁z + D₁ = 0

N1 = {A₁; B₁; C₁}

α₂: A₂x + B₂y + C₂z + D₂ = 0

N₂ = {A₂; B₂; C₂}

Пусть угол φ = α₁;α₂ = N₁;N₂

5) а) Пусть α₁ || α₂

α₁ || α₂ => N₁ || N₂ <=> N1×N2 = 0

б) Пусть α₁┴α₂

α₁┴α₂ => N₁┴N₂ <=> N₁∙N₂ = 0

A₁A₂ + B₁B₂ + C₁C₂ = 0

6) Пусть плоскость задана общим уравнением

α: Ax + By + Cz + D = 0

Расстоянием от точки до плоскости называется длина перпендикуляра, опущенного из точки на плоскость

КРИВЫЕ ВТОРОГО ПОРЯДКА

Ax² + 2Bxy + Cy² + 2Dx + 2Ey + F = 0

Коэффициенты уравнения – действительные числа, но по крайней мере одно из чисел А, В

и С отлично от нуля. Такие линии называются линиями второго порядка. Это уравнение определяет на плоскости окружность, эллипс, гиперболу или параболу. Уравнение

Ax² + 2Bxy + Cy² + 2Dx + 2Ey + F = 0 всегда определяет: либо окружность (при А=С), либо эллипс (при А∙С>0), либо гиперболу

(при А∙С<0), либо параболу (А∙С=0). При этом возможны случаи вырождения: для эллипса

(окружности) – в точку или мнимый эллипс

(окружность), для гиперболы – в пару пересекающихся прямых, для параболы – в пару параллельных прямых.

   

ОКРУЖНОСТЬ

Простейшей кривой 2го порядка является окружность. Окружность это множество всех точек М равноудаленных от центра, удовлетворяющих условию М₀М=R. Пусть точка М₀ в прямоугольной системе координат

ОХУ имеет координаты х₀у₀, а М(х;у) – произвольная точка окружности. Тогда из условия М₀М=R получаем ур-е

(x – x_о)² – (y – y_о)² = R² – каноническое уравнение окружности. Если координаты центра окружности О(0;0), то х² +у² = R². Этому уравнению удовлетворяют координаты любой точки данной окружности и не удовлетворяют координатам точки не лежащей на окружности. Раскрыв скобки получим:

x² + y² - 2x_ox - 2y_oy + x_o² + y_o² - R² = 0. Подставив в общее уравнение кривой 2го порядка (Ax² + 2Bxy + Cy² + 2Dx + 2Ey + F = 0) значения

В=0 и А=С≠0, получим: Ax² + Аy² + 2Dx + 2Ey + F = 0

уравнение определяет окружность при условии

Ее центр находится в точке О₁(), а радиус

. Если , то

. Ему удовлетворяют координаты единственной точки О₁(). В этом случае говорят:

«окружность выродилась в точку»(имеет нулевой радиус). Если

, то уравнение не определяет никакой линии, т.к. правая часть уравнения отрицательная, а левая не отрицательная (говорят: «окружность мнимая»)

   

ЭЛЛИПС

Эллипсом называется множество всех точек плоскости, сумма расстояний от каждой из двух данных точек этой плоскости, называемых фокусами, есть величина постоянная, большая, чем расстояние между фокусами. Пусть М(х;у) это произвольная точка эллипса. F₁, F₂ – фокусы; 2с – расстояние между F₁ и F₂;

2а - сумма расстояний от произвольной точки эллипса до фокусов

MF₁ + MF₂ = 2a

. Т.к. a > c, то а² - с² > 0. а² - с² = b². Тогда b²x²+a²y²=a²b² или

- каноническое уравнение эллипса.

Форма эллипса зависит от отношения b/a. При b=a эллипс превращается в окружность, ур-е эллипса принимает вид х² + у² = а².

Отношение с/а половины расстояния между фокусами к большой полуоси эллипса называется эксцентрисетом эллипса. ε=с/а.

Отсюда видно, что чем меньше ε, тем эллипс будет менее сплющенным. Если ε=0, то эллипс превращается в окружность.

Прямые х=±а/ε называются директрисами эллипса.

ГИПЕРБОЛА

Гиперболой называется множество всех точек плоскости, модуль разности расстояний от каждой из которых до двух данных точек этой плоскости, называемых фокусами, есть величина постоянная, меньшая, чем расстояние между фокусами. F₁, F₂ - фокусы гиперболы; 2с – расстояние между фокусами; 2а – модуль разности расстояний от каждой точки гиперболы до фокусов.

2а<2с. Пусть М(х;у) – произвольная точка гиперболы.

|MF₁ – MF₂| = 2a или MF₁ – MF₂ = ±2a, т.е.

 - каноническое уравнение гиперболы

b² = c² - a². Точки А₁(а;0) и А₂(-а;0) называют вершинами гиперболы, а отрезок А₁А₂ = 2а – действительной осью. Отрезок В₁В₂ (В₁В₂ = 2b), соединяющий B₁(0;b) и B₂(0;-b) называется