Косой изгиб представляет собой разновидность поперечного изгиба, при котором плоскость действия нагрузки не совпадает ни с одной из главных осей инерции поперечного сечения стержня. Разложение нагрузки по направлению главных осей инерции сечения приводит к возникновению двух плоских изгибов. Нормальные напряжения вычисляются по формуле:
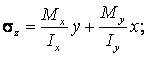 (2.1)
(2.1)
где ![]()
![]() ,
,
M – суммарный изгибающий момент, j – угол, образованный вектором нагрузки и главной осью y.
Условие прочности запишется в виде[1]:
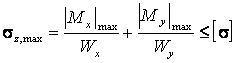 .
(2.2)
.
(2.2)
Три типа задач, вытекающих из условия прочности:
1. проверка
прочности:![]() ,
,
2. подбор поперечного сечения:
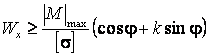 , (2.3)
, (2.3)
где 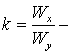 известный
числовой множитель,
известный
числовой множитель,
3. определение грузоподъемности:
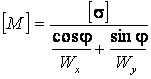 (2.4)
(2.4)
2.1.2. Внецентренное растяжение-сжатие.
Такой вид деформации возникает
при приложении к стержню сил, параллельных его продольной оси, но смещенных
относительно последней на величину e
(эксцентриситет). В поперечных сечениях стержня возникают три внутренних
усилия: продольная сила Nz=P, изгибающие моменты Mx=Pyp, My=Pxp![]() (xp,yp-координаты
точки приложения внецентренной силы).
(xp,yp-координаты
точки приложения внецентренной силы).
Формула для определения нормального напряжения запишется в виде:
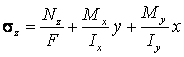 ,
(2.5)
,
(2.5)
Подстановка ![]() в формулу (2.5) дает
в формулу (2.5) дает
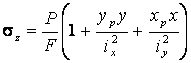 ,
(2.6)
,
(2.6)
где 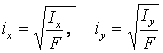 - радиусы инерции
поперечного сечения стержня.
- радиусы инерции
поперечного сечения стержня.
Условие прочности:
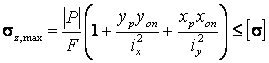 , (2.7)
, (2.7)
где ![]() координаты
опасной точки сечения.
координаты
опасной точки сечения.
Положение опасной точки определяется с помощью нейтральной оси.
Уравнение нейтральной оси
![]() или
или 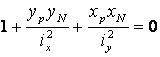 ,
(2.8)
,
(2.8)
При внецентренном растяжении-сжатии нейтральная ось не проходит через центр сечения. Отрезки, отсекаемые нейтральной осью от осей x, y определяются по формулам:

Опасной точкой поперечного сечения является точка, наиболее удаленная от нейтральной оси.
Из условия прочности (2.7) непосредственно следует формула определения грузоподъемности стержня
 (2.9)
(2.9)
2.1.3. Изгиб с кручением.
В условиях совместного действия изгибающего и крутящего моментов работают многие элементы конструкций и деталей машин.
Для стержней кругового
поперечного сечения распределение нормальных и касательных напряжений по высоте
сечения приведено на рис.2.1. ![]()
Опасными точками сечения являются крайние точки вертикального диаметра, в которых возникают максимальные нормальные напряжения и максимальные касательные напряжения кручения. Проверка прочности материала, который одновременно испытывает действие нормальных и касательных напряжений, производится по формуле
![]() ,
,
где ![]() -
расчетные напряжения, соответствующие i-ой классической теории прочности.
(Изложение классических теорий прочности можно найти в любом учебнике по
сопротивлению материалов).
-
расчетные напряжения, соответствующие i-ой классической теории прочности.
(Изложение классических теорий прочности можно найти в любом учебнике по
сопротивлению материалов).
|
|
|
Рис. 2.1 |
Для проверки прочности пластичного материала вычисляются расчетные напряжения, соответствующие третьей или четвертой теориям прочности
![]() (2.10)
(2.10)
![]() (2.11)
(2.11)
Подстановка в формулы (2.10) и
(2.11) значений напряжений 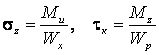 (Ми –
суммарный изгибающий момент, вычисляется по формуле
(Ми –
суммарный изгибающий момент, вычисляется по формуле ![]() )
дает
)
дает
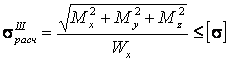 (2.12)
(2.12)
 (2.13)
(2.13)
2.2. Определение перемещений в балках.
В балках под нагрузкой происходит
искривление оси, в результате чего возникают вертикальные перемещения v
(прогибы) точек оси и углы поворота ![]() поперечных
сечений (рис. 2.2).
поперечных
сечений (рис. 2.2).
Для определения прогибов v(z) и углов поворота![]() применяются метод начальных
параметров и интеграл Мора.
применяются метод начальных
параметров и интеграл Мора.
|
|
|
Рис.2.2 |
2.2.1. Метод начальных параметров.
Непосредственно из
рассмотрения рис.2.2 в предположении малости углов поворота (![]() ) следует связь между величинами v(z) и
) следует связь между величинами v(z) и ![]()
![]() (2.14)
(2.14)
Производная от функции
угла поворота по координате оси балки определяет кривизну ![]() изогнутой оси
изогнутой оси
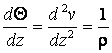 (2.15)
(2.15)
Кривизна связана с функцией изгибающего момента Mx зависимостью
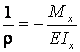 (2.16)
(2.16)
где ![]() ‑
изгибная жесткость балки.
‑
изгибная жесткость балки.
Комбинирование формул (2.15) и (2.16) приводит к выражению, известному как приближенное дифференциальное уравнение изогнутой оси стержня
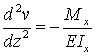 (2.17)
(2.17)
В результате двукратного интегрирования уравнения (2.17) имеем
 (2.18)
(2.18)
где v0 ,![]() -
постоянные интегрирования, соответствующие прогибу и углу поворота начального
сечения балки.
-
постоянные интегрирования, соответствующие прогибу и углу поворота начального
сечения балки.
Функция прогибов для балки с несколькими участками записывается в виде
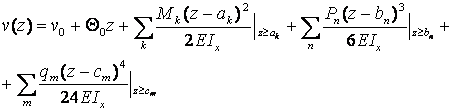 (2.19)
(2.19)
где ak,, bn– координаты точек приложения сосредоточенных моментовMk и сил Pn , , cm - координата начала приложения распределенной нагрузки qm.
Функция угла поворота, согласно формуле (2.14), определяется дифференцированием функции прогибов и для балки с несколькими участками имеет вид
 (2.20)
(2.20)
Пример
1. Имеется однопролетная балка с консолью (рис.2.3). Требуется определить
прогиб свободного края консоли (сечение А) и угол поворота опорного сечения В
методом начальных параметров. В расчете принимается изгибная жесткость балки
равная ![]() .
.
Вертикальные реакции опор ![]() и
и
![]() одинаковые и равны
одинаковые и равны ![]() .
.
|
|
|
Рис.2.3 |
Правило знаков: положительным прогибам соответствуют перемещения точек оси балки вертикально вниз; с учетом зависимости (2.14), положительному углу поворота соответствует поворот касательной, проведенной к оси балки в заданном сечении, по часовой стрелке.
Искомый
прогиб определяется по формуле (2.19), в которой следует принять ![]() (прогиб на шарнирной опоре равен
нулю),
(прогиб на шарнирной опоре равен
нулю),
![]()
![]() ,
,
![]() ,
, ![]()
![]()
Неизвестный начальный
угол поворота ![]() определяется из граничного
кинематического условия (кинематическое граничное условие – уравнение,
составленное для определения перемещений любого сечения балки с известным
значением прогиба или угла поворота);
определяется из граничного
кинематического условия (кинематическое граничное условие – уравнение,
составленное для определения перемещений любого сечения балки с известным
значением прогиба или угла поворота);
при ![]()
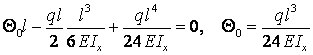
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.