использовании ДПФ чаще всего возникают три проблемы: появление ложных спектральных составляющих, замывание спектральных составляющих, паразитная амплитудная модуляция спектра (искажение). Рассмотрим эти явления подробнее.
1.Появление ложных спектральных составляющих (рис. 4) – это явление, при котором высокочастотные компоненты функции времени могут быть приняты за низкочастотные. Причина – недостаточная частота дискретизации (неправильный выбор ωв ).
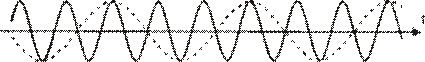
Рис. 4. Появление ложных спектральных составляющих
2.Размывание спектральных составляющих. Это явление возникает из-за того, что анализируется ограниченный массив данных. Отбрасывается все, что происходит до и после периода наблюдений, что эквивалентно умножению сигнала на прямоугольную выделяющую функцию с соответствующим изменением спектра (рис. 5).
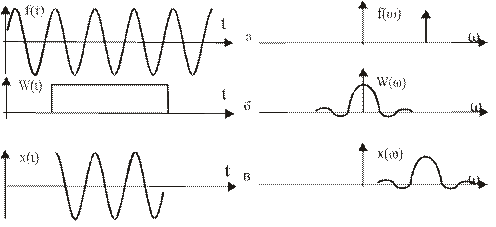
Рис. 5. Размывание спектральных составляющих: а – непрерывный сигнал и его спектр; б – прямоугольная выделяющая функция и ее спектр; в – результирующий сигнал и его спектр
Стандартный способ уменьшения этого явления – умножение сигнала на такую выделяющую функцию, которая имеет меньшие боковые лепестки. Однако снижение уровня боковых лепестков дается ценой расширения главного лепестка спектра окна, что приводит к ухудшению разрешения. Следовательно, необходим какой-то компромисс между шириной главного лепестка и уровнем подавления боковых лепестков. Существует много выделяющих функций, обладающих различными свойствами.
3.Паразитная амплитудная модуляция спектра. Каждому коэффициенту Фурье соответствует фильтр с частотной характеристикой
![]() K(
)ω вида sin
x x (рис. 6, а). Это справедливо для случая прямоугольной выделяющей функции.
K(
)ω вида sin
x x (рис. 6, а). Это справедливо для случая прямоугольной выделяющей функции.
![]() Главные лепестки
представляют собой N независимых фильтров. Входной сигнал exp(j
tω )
с частотой, кратной 1Δt
, пройдет через соответствующий фильтр без изменений. Другие фильтры его подавят.
Главные лепестки
представляют собой N независимых фильтров. Входной сигнал exp(j
tω )
с частотой, кратной 1Δt
, пройдет через соответствующий фильтр без изменений. Другие фильтры его подавят.
![]() Эффект паразитной
модуляции проявляется, когда вычисляются спектральные составляющие на частотах,
не совпадающих с частотами, кратными 1Δt
. В наихудшем случае, когда рассчитывается сигнал между фильтрами, его уровень
равен 0,647. Избежать этого эффекта можно двумя путями:
Эффект паразитной
модуляции проявляется, когда вычисляются спектральные составляющие на частотах,
не совпадающих с частотами, кратными 1Δt
. В наихудшем случае, когда рассчитывается сигнал между фильтрами, его уровень
равен 0,647. Избежать этого эффекта можно двумя путями:
-
![]() рассчитывать
спектры на частотах, кратных частоте 1Δt
;
рассчитывать
спектры на частотах, кратных частоте 1Δt
;
- если необходимо вести расчеты и на других частотах, то массив из N1 исходных данных дополняют N2 нулями, т.е. увеличивают период повторения исходного сигнала. При этом число фильтров ДПФ увеличивается, а расстояние Δ f между центральными частотами уменьшается (рис. 6 б)
![]()
![]() Δ f =1 T =1 N1Δt, Δ f ′ =1 T =1 (N1
+ N2)Δt .
Δ f =1 T =1 N1Δt, Δ f ′ =1 T =1 (N1
+ N2)Δt .
![]() Полоса
пропускания фильтра не изменяется, т.к. она определяется величиной 1Δt .
Полоса
пропускания фильтра не изменяется, т.к. она определяется величиной 1Δt .
При N1= N2 передаточные функции K(ω) имеют вид:
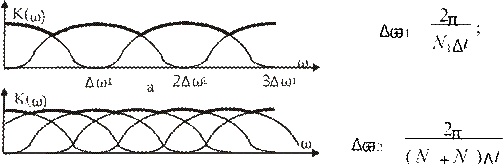 Δω2 2Δω2 3Δω2 4Δω2 5Δω2 6Δω2 1 2
Δω2 2Δω2 3Δω2 4Δω2 5Δω2 6Δω2 1 2
б .
Рис. 6. Частотная характеристика ДПФ: а - N1 отсчетов; б - N1 отсчетов и N2 нулей
Алгоритм ДПФ имеет существенный недостаток: большое число вычислительных операций. Для вычисления всех N спектральных коэффициентов требуется N2 умножений и столько же сложений.
Поэтому на практике часто применяют быстрое преобразование Фурье (БПФ). Суть этого алгоритма заключается в многократном членении заданной последовательности временных отсчетов на более короткие последовательности. Поясним достигаемый при этом выигрыш на примере одного первого разбиения.
Пусть задана последовательность отсчетов х(k),
k = 0,1,...,
N −1, причем
N = 2r
, где r - целое число. Разобьем эту последовательность на две последовательности, содержащие соответственно
четные отсчеты хI (k)= x(2k)
и нечетные отсчеты хII ( )k = x(2k
+1).
Введем обозначение WN
=exp(− πj2 ![]() N).
С учетом равенств WN2 =WN
N).
С учетом равенств WN2 =WN![]() 2 ; WN2kn = WN
2 ; WN2kn = WN![]() 2kn для четной последовательности
отсчетов ДПФ имеет вид:
2kn для четной последовательности
отсчетов ДПФ имеет вид:
![]() N 2 1− N 2 1− n =01, ,..., N
N 2 1− N 2 1− n =01, ,..., N![]() 2 1− .
2 1− .
k=0 k=0
Для нечетной последовательности отсчетов ДПФ имеет вид:
N![]() 2 1− N
2 1− N![]() 2 1−
2 1−
∑ x(2k +1)WN(2 1k+ )n =WNn ∑ xII ( )k WN 2kn =WNn SII ( )n ,
k=0 k=0 n =01, ,..., N![]() 2 1− .
2 1− .
Фазовый множитель WNn =exp(− j n2 π![]() N)
перед второй суммой учитывает задержку последовательности {xII
(п)}
на один интервал относительно последовательности {x nI
(
)}.
N)
перед второй суммой учитывает задержку последовательности {xII
(п)}
на один интервал относительно последовательности {x nI
(
)}.
Спектры S nI
(
) и SII
(n)
также периодические, но с периодом N![]() 2
.
2
.
![]() Найдем результирующий
спектр. Для частот τ = 0,1,...,
N 2 −1 учтем
периодичность спектров S nI ( )= S n NI
(
−2);
Найдем результирующий
спектр. Для частот τ = 0,1,...,
N 2 −1 учтем
периодичность спектров S nI ( )= S n NI
(
−2);

![]() SII
(
)n = SII
(n
− N 2).
Кроме того, надо учитывать перемену знака перед фазовым множителем при n ≥ N2:
SII
(
)n = SII
(n
− N 2).
Кроме того, надо учитывать перемену знака перед фазовым множителем при n ≥ N2:
WNn =WNN 2+ −n N 2 =WN
N 2WNn N− ![]() 2 = −WNn N−
2 = −WNn N− ![]() 2,
2,
![]()
т.к. WN N2 = exp[(− j2π N N)( 2)]= exp(− jπ = −) 1.
В результате получаем выражение для вычисления всей последовательности отсчетов спектра:
S n
![]() (
)=⎧⎪⎨S
nII (( )−+NWN2n)S−IIW(nN)n
N, S n N
2 , 0N≤ ≤2n
≤ −NN 21.−1;
(2)
(
)=⎧⎪⎨S
nII (( )−+NWN2n)S−IIW(nN)n
N, S n N
2 , 0N≤ ≤2n
≤ −NN 21.−1;
(2)
⎪⎩S
n ![]()
![]()
Это основное расчётное соотношение для БПФ. Спектр S n( ) содержит N спектральных отсчетов на интервале одного периода по оси n .
![]() Подсчитаем число
операций, необходимых для получения N спектральных коэффициентов при использовании
этого метода. Для вычисления функций S nI ( ) и SII (n)
требуется (N
2)2
умножений
Подсчитаем число
операций, необходимых для получения N спектральных коэффициентов при использовании
этого метода. Для вычисления функций S nI ( ) и SII (n)
требуется (N
2)2
умножений
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.