Цель работы: Изучение теоретических и практических приёмов решения задач линейного программирования.
Постановка задачи: Используя данные из таблицы П.1, найти оптимальное решение для maxF.
|
3 |
maxF=3x1+3x2 |
x1-4x2≤4, 3x1+2x2≤6, -x1+x2≤1, x1+2x2≥2 |
Ход работы:
Для решения задачи был выбран графический метод, т.к. он наиболее нагляден. Ограничения принимают следующий вид:
Х2 =x1/4-1; (1)
Х2 = 3-3х1/2; (2)
Х2 = 1+х1; (3)
Х2 = 1-х1/2; (4)
Построили график функции по указанным ограничениям, получив при этом четырехугольник – пространство решений:
 |
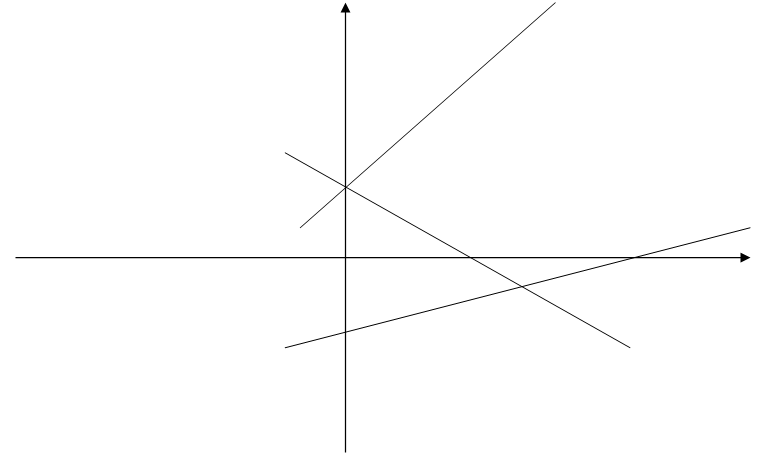
Рисунок 1. График функции задачи
Далее было необходимо подставить координаты 3-ёх точек, являющихся вершинами треугольника в уравнение maxF=3x1+3x2 . В моём случае одно из ограничений не попало в ту часть, где находится основной график. Чтобы определить координаты точек A, B, C, необходимо решить системы уравнений, решениями которых являются точки пересечений графиков функций ограничений. Для точки А система выглядит следующим образом:
х2=1-х1
х2=1-х1/2
Отсюда координаты точки A: (0;1).
Для точки B система выглядит следующим образом:
х2=1+х1
х2= 3-3х1/2
Отсюда координаты точки B: (0,8;1,8).
Для точки С система выглядит следующим образом:
х2=3-3х1/2
х2=1-х1/2
Отсюда координаты точки С: (2;0).
Подставляем координаты точек в уравнение maxF=3x1+3x2 и получил:
A(0; 1) : maxF=3
B(0,8;1,8): maxF=7,8
C(2;0): maxF=6
В итоге, получаем, что оптимальное решение находится в точке С(0,8;1,8).
Проведем анализ на чувствительность. Для этого будем увеличивать наши дефицитные значения, и уменьшать недефицитные. Возьмём точку оптимального решения и начнем параллельно переносить её график до пересечения с прямой (1). Найдем координаты точки пересечения:
х1=4; х2=0;
Теперь, когда мы имеем эти координаты, можно найти максимально изменение ресурса, изменение дохода и ценность ресурса.
∆zi= 4-39/7=-12/7
∆i= 4-6=-2
yi=∆zi/∆i=-12/7*(-1/2)=6/7
По аналогии находим данные характеристики и для других условий. Х1=4; х2=3. Результаты вычислений представлены в таблице 1.
|
РРесурс |
Тип |
Max изменение ∆i ресурса |
Изменение дохода ∆zi |
Ценность yi=∆zi/∆i |
|
1 |
Дефицит |
-2 |
-12/7 |
6/7 |
|
2 |
Дефицит |
2 |
23/5 |
23/10 |
Теперь найдем допустимые изменения коэффициентов целевой функции. Вариация коэффициентов может привести к другому решению, поэтому обычно решается вопрос: каков диапазон изменения коэффициентов целевой функции не меняющий решения. Изменение одного из коэффициентов целевой функции меняет угол наклона прямой, не изменяя при этом точку оптимума, что приводит к вращению прямой вокруг точки оптимума в секторе прямых, определяющих решение.
Записав целевую функцию в виде z=C1x1+C2x2 фиксируя один из коэффициентов и приравнивая поочередно к прямым (2) и (4), находим допустимый диапазон. Таким образом получаем следующие интервалы:
|
Коэффициент |
Min |
Max |
|
C1 |
1 |
1,5 |
|
C2 |
3 |
4,5 |
Вывод: Изучили теоретические и практические приёмы решения задач линейного программирования графическим методом.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.