


Задача 2.
Решение этой задачи
требует знания понятия производной высших порядков. Напомним, что производная
порядка n обозначается ![]() или
или
![]() . Общая формула вычисления
производных высших порядков выглядит следующим образом
. Общая формула вычисления
производных высших порядков выглядит следующим образом ![]() =
=![]() .
.
Задача. Найти ![]() , если
, если ![]()
Решение. Напомним, что вторая производная есть первая производная от первой производной функции:
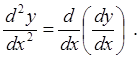 Найдем первую производную
функции:
Найдем первую производную
функции:
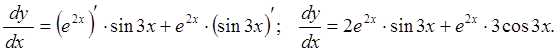
А теперь еще раз продифференцируем полученную функцию:
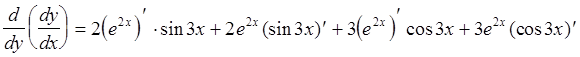 =
=
=![]() .
.
Итак, после приведения подобных слагаемых имеем искомую производную:
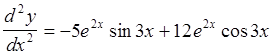 .
.
Задача. Найти ![]() , если
, если ![]() .
.
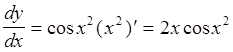 .
.
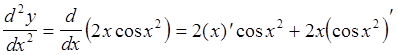 =
=![]() .
.
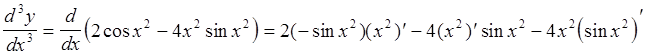 =
=
=![]() .
.
Задача 3.
Решение этой задачи требует владения техникой дифференцирования функций заданных параметрически. Применение этих правил мы покажем на решении конкретной задачи.
Задача. Найти ![]() и
и ![]() для
функции, заданной параметрически уравнениями:
для
функции, заданной параметрически уравнениями:
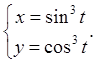
Решение. Первая производная функции, заданной параметрически находится по формуле:
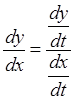 , где
, где 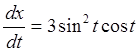 и
и 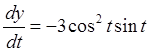 , тогда
, тогда
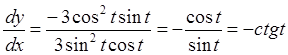 . Чтобы вычислить вторую
производную
. Чтобы вычислить вторую
производную ![]() , представим первую
производную
, представим первую
производную ![]() как некоторую функцию,
заданную параметрически и возьмем от нее первую производную по переменной
как некоторую функцию,
заданную параметрически и возьмем от нее первую производную по переменной ![]() :
:
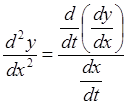 , где
, где 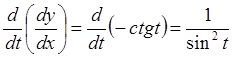 , тогда
, тогда
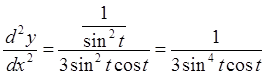 .
.
Задача. Найти ![]() и
и ![]() для
функции, заданной параметрически уравнениями:
для
функции, заданной параметрически уравнениями:
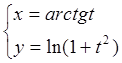
Поскольку 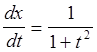 ,
, 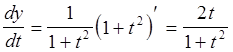 ,
то
,
то 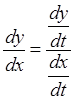 =2t.
=2t.
Тогда 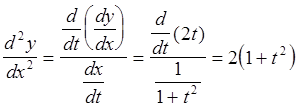 .
.
Задача 4.
Прежде чем перейти к решению этой задачи, напомним геометрический смысл производной.
Производная в данной точке равна тангенсу угла наклона к оси Х касательной к графику функции , проведенной в этой точке.
Задача. Найти уравнение касательной и нормальной прямой для графика функции, заданной параметрически уравнениями:
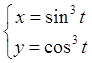 при
при ![]() .
.
Решение. Уравнение касательной имеет вид:
![]() .
.
Нормальная прямая
перпендикулярна касательной и имеет угловой коэффициент 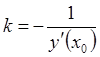 , уравнение нормали таково:
, уравнение нормали таково:
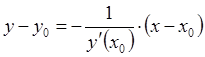 .
.
Вычислим координаты
точки ![]() , соответствующей значению
параметра
, соответствующей значению
параметра ![]() :
:
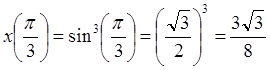 ,
, 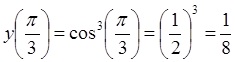 .
.
Производная ![]() была найдена в предыдущей
задаче. Она равна
была найдена в предыдущей
задаче. Она равна 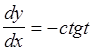 .
.
вычислив ее значение
при ![]() , получаем
, получаем 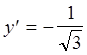 .
.
Тогда уравнение касательной имеет вид:
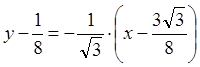 .
.
Уравнение нормали соответственно:
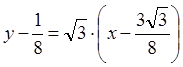 .
.
Задача 5. Найти ![]() и
и
![]() для функции
для функции ![]() , заданной неявно следующим
уравнением:
, заданной неявно следующим
уравнением:
![]() в точке М(1;2).
в точке М(1;2).
Решение . Продифференцируем уравнение, задающее
функцию![]() , помня о том, что
, помня о том, что
![]() -- функция переменной
-- функция переменной ![]() :
:
![]() ,
,
![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.