Понятие скалярного, векторного и смешанного произведения векторов. Скалярное произведение векторов

Глава 3 Понятие скалярного, векторного и смешанного произведения векторов.

3.1 Скалярное произведение векторов.

В главе 1 была введена операция умножения вектора на число. Теперь же введём в рассмотрение скалярное произведение двух векторов  и .

Определение:Скалярным произведением двух векторов и называется число равное произведению длин этих векторов на косинус угла между ними.

Будем обозначать скалярное произведение -

Таким образом:

-угол между векторами и

Скалярное произведение обладает следующими свойствами.

Свойство 1:   переместительное свойство

Свойство 2:   Скалярное произведение равно модулю одного из векторов умноженному на проекцию другого вектора на направление первого

Свойство 3:   Распределительное свойство

Свойство 4:   Пусть и - скаляры

Свойство 5: Чтобы векторы и были перпендикулярны необходимо и достаточно чтобы их скалярное произведение было равно нулю

Если векторы и  заданы своими координатами, то можно получить правило вычисления скалярного произведения.

Пусть:        

                 

  Используя полученную формулу, можно получить другие полезные формулы, часто применяемые при решении различных задач.

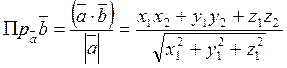
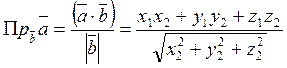
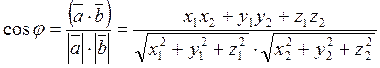
3.2 Векторное произведение

Пусть даны два вектора и .

Определение: Векторным произведением двух векторов и  называется вектор , обладающий следующими свойствами.

1.  Модуль вектора  равен произведению модулей векторов и на синус угла между ними

2.  Вектор  перпендикулярен векторам и .

3.  Вектор  направлен таким образом, что для наблюдателя находящегося в его конце кратчайший поворот первого вектора  к второму вектору  должен происходить против хода часовой стрелки (см. рис. 3.1)

    

                                                                                                         

 

        

Рис 3.1

Будем обозначать векторное произведение  проще .

Свойства векторного произведения.

Свойство 1:   Если векторы и не коллинеарны, то модуль векторного произведения равен площади параллелограмма построенного на векторах  и .

        B                                          C

                             

 

A                                       D

Рис 3.2

Свойство 2:   Векторное произведение векторов и равно нулю тогда и только тогда когда векторы и  коллинеарны.

Свойство 3:   При перестановке векторов и векторное произведение этих векторов меняет знак на противоположенный.

Свойство 4:   Пусть и  - числа

Свойство 5:   Распределительное свойство

Если векторы и заданы своими координатами , , то их векторное произведение:

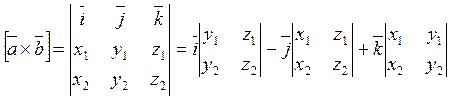
- единичные векторы лежащие на осях ОХ, ОУ, OZ направленные вдоль оси декартовой системы координат.

3.3 Смешанное произведение трёх векторов.

  Прежде чем дать определение смешанного произведения, введём в рассмотрение понятие правой и левой тройки векторов. Пусть три вектора  с общим началом не лежат в одной плоскости.

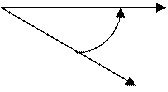
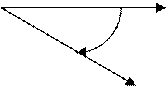
Определение: Тройка векторов  называется правой (левой) тройкой если для наблюдателя, находящегося в конце третьего вектора , кратчайший поворот от первого вектора  ко второму вектору  происходит против хода часовой стрелки. На Рис. 3.3 показана правая тройка , на Рис. 3.4 левая тройка .

                                                         

 

Рис 3.3

        

 

Рис 3.4

Определение: Смешанным произведением трёх векторов  называется число равное скалярному произведению векторов  и .

Смешанное произведение трёх векторов обозначается  или  таким образом по определению

где  - угол между векторами  и .

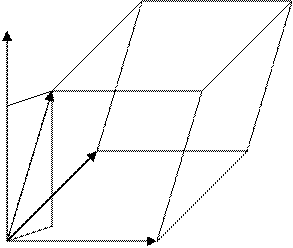
  Очень важным при решении задач является геометрический смысл смешанного произведения. Пусть три вектора  имеют общее начало и не лежат в одной плоскости. Построим на этих векторах как на рёбрах параллелепипед  (Рис. 3.5)

B₁                                         C₁

 

A₁                             D₁        

                                                                                                  

                                                    B                         C

A                           D

Рис. 3.5

  По определению смешанного произведения

Величина  геометрически выражает площадь параллелограмма АВСD.

  Величина   является проекцией вектора  на направление вектора , причём если угол - острый, то , если  - тупой то ,  - высота параллелепипеда, таким образом

легко видеть, что если векторы  образуют правую тройку то угол - острый и имеем знак плюс, в случае же если векторы  образуют левую тройку то угол   - тупой и имеет знак минус.

  Таким образом, смешанное произведение трёх векторов  равно объёму параллелепипеда, построенного на этих векторах, и взятого со знаком плюс, если векторы  образуют правую тройку и со знаком минус если векторы образуют левую тройку.

  Очень важно уметь вычислять смешанное произведение в случае если векторы  заданы своими координатами.

,

,

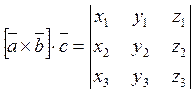
Ещё одним свойством смешанного произведения является его связь с понятием компланарности векторов.