Метод канонических корреляций. Пример решения типовой задачи. Проведение канонического анализа на компьютере, страница 2

S₂₂ - ковариационная матрица исходных результативных переменных  (Y₁, Y₂,   Y_p ) размерности (p × p),

S_12, S₂₁ - ковариационные матрицы исходных переменных (Х₁, Х₂... X_q )  и   (Y₁, Y₂  ... Y_p) соответственно, размерности  (q × p)  и  (p × q).

В матрицах S₁₁ и S₂₂  элементы, расположенные на главной диагонали, являются дисперсиями соответствующих переменных. Все остальные элементы матрицы S представляют  собой  значения ковариаций пар переменных. Представим выражение  (8.1)  в матричном виде:

U = XA,   V = YB,

где  U, V  - векторы значений канонических переменных,

Х, Y  - матрицы исходных значений переменных,

A, B  - векторы коэффициентов канонических переменных.

Если предположить, что средние значения канонических переменных U и V равны нулю, а их дисперсии равны единице, то формулу для расчета канонических коэффициентов корреляции можно записать следующим образом:

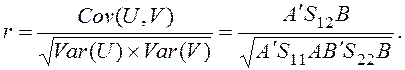                               (8.5)

Для упрощения процедуры вычисления оптимальных коэффициентов канонических переменных предположим, что каждая из этих переменных  имеет единичную дисперсию и нулевое математическое ожидание. Тогда можем записать:

    и      

откуда .

Максимальный канонический коэффициент  корреляции  рассчитывается по формуле:

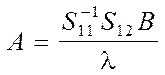.                                                                      (8.6)

Для того,  чтобы найти компоненты вектора A, необходимо определить векторы  B  и . Значения  находим как собственные числа матрицы С= Размерность этой матрицы равна  (p×p)(p×q)(q×q)(q×p), следовательно, можно вычислить собственные числа () и соответствующие им собственные векторы B_j. Подставляя поочередно полученные значения  и  B_j  в выражение (8.6), вычислим вектор  A_jи соответствующий канонический коэффициент корреляции  r_j.

Канонические коэффициенты  корреляции можно рассчитывать и исходя из выборочной матрицы корреляционной (R):

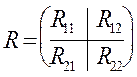.                                                                           (8.7)

При этом все рассуждения и выкладки аналогичны тем, которые приведены выше для ковариационной матрицы. Но значения коэффициентов канонических переменных  a_i  (  и  b_j  ) будут отличаться.  

Если коэффициенты канонических переменных были вычислены на основании ковариационной матрице  S, то они относятся к исходным переменным - X_i  и  Y_j.  Если расчет этих коэффициентов осуществлялся на основе корреляционной матрицы R, то они относятся к стандартизованным значениям исходных переменных:           ;             .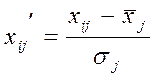

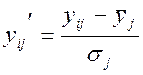Для проверки значимости коэффициентов канонической корреляции используется критерий Бартлетта.

Проверить нулевую гипотезу о том, что множество переменных  X₁, X₂,... X_q  не коррелирует с множеством переменных Y₁, Y₂ ... Y_p , можно при помощи c² -критерия:

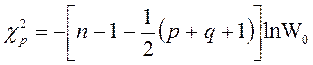                                            (8.8)

где  .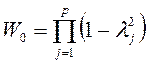

Если  c²  расчетное больше табличного значения критерия при выбранном уровне значимости и с числом степеней свободы равным  (p×q), то можно утверждать, что, по крайней мере первый канонический коэффициент корреляции  r₁  = , будет отличен от нуля.

Чтобы проверить значимость второго коэффициента канонической корреляции, необходимо рассчитать по формуле:

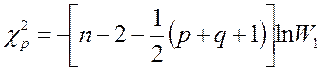                где  .

В этом случае, если c² расчетное больше табличного значения критерия при выбранном уровне значимости и с числом степеней свободы равным

(p–1)(q–1), то можно утверждать, что второй канонический коэффициент корреляции  r₂  = , также будет отличен от нуля. Значимость оставшихся коэффициентов проверяется  аналогично.

8.2. Пример решения типовой задачи

Пример

На основании нижеприведённых данных вычислим канонические коэффициенты корреляции для двух групп переменных