Оптимальное размещение взаимосвязанных объектов на древовидных сетях с ограничениями на расстояния, страница 2

На втором этапе задача (2.1)—(2.3) решается следующим образом. Функция

min [L(Es, :  vt)l

s,te

является вогнутой неубывающей кусочно-линейной функцией. Из условий (2.4) следует, что z* = min{z I F(z) = 0}. Интервал линейности функции F(z), которому принадлежит z*, находится с помощью бинарного поиска по значениям z на заданной сетке значений с использованием процедуры SLP. Значение z* находится из условий (2.4), а оптимальное размещение для — с помощью процедуры SLP. Трудоемкость алгоритма равна О(п(т + + п logM )), где М — максимум числителей и знаменателей рациональных исходных данных.

Предлагается следующий модифицированный бинарный алгоритм (МБА) для решения задачи (2.1)—(2.3). На первом этапе также находится интервал [Ч, zU], содержащий z*. На втором этапе производится поиск z* при помощи деления пополам. Если для текущего не существует допустимого решения, то с помощью модификации процедуры SLP из [4] определяется пара вершин vs, vt, для которых нарушены условия (2.4). Нас интересуют только кратчайшие прямые пути между Es и Et, поэтому из сети N(z) можно удалить все узлы Ц, i s, t,PI тогда получим сеть Nvt(z). Далее алгоритмом из [5] находится кратчайший путь в сети Nst(z') между узлами Ц, Et, длина которого равна линейной функции А: + В.

Записываем модель ЛП поиска кратчайшего пути [5] между парой узлов (Ц, Et) в сети ( ⁷ ) считая параметром. Для этого вводим ориентацию на дугах сети Nst(z). Узел Es — источник, а Ег сток; дуги, инцидентные узлу Ц, — выходящие из Ея, а дуги, инцидентные Ц, входящие в этот узел. Дуги, соединяющие узлы и АЛ, заменяются парой дуг.

46 МЗ

                            ОПТИМАЛЬНОЕ РАЗМЕЩЕНИЕ НА ДРЕВОВИДНЫХ СЕТЯХ ОБЪЕКТОВ                                                         397

Обозначим через С; = i = s, t, 1, 2,  2п + — 1), матрицу инциденций узлов и дуг сети Nst(z):

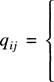+1, если дуга е. выходит из узла с номером i, —1, если дуга е. входит в узел с номером i,

0 иначе.

Пусть первая строка матрицы R соответствует узлу Ц, а вторая — узлу Et. Обозначим через h(z) вектор весов дуг сети Nst(z) и свяжем с каждой дугой еј переменнуюЛ, представляющую собой поток продукта по этой дуге, af— вектор-столбец, в котором Кя компонента равна Л. Цепь из Es в Et можно рассматривать как поток единицы продукта, выходящий из источника и приходящий в сток. Тогда задача о кратчайшем пути формулируется как задача о нахождении потока минимальной стоимости:

                                                                  (h(z),f)        min,

                                                                                                     (2.5)

Запишем задачу, двойственную задаче (2.5), приписав каждому узлу с номером i переменную Ъ: is — it —» тах,         (2.6)

АЛ h(z).

С помощью двойственной задачи и условий дополняющей нежесткости из [5] находим интервал [4, ф], на котором найденный для z' путь остается кратчайшим. Отметим, что на этом интервале функция L(Es, Ет : z) линейная и равна Az + В. Решаем уравнение

                                                              Az + В = d(vs, vt)                                              (2.7)

и получаем значение z”. Существование допустимого решения для z” проверяется процедурой SLP. Далее определяем, является ли z” оптимальным в задаче (2.1)—(2.3), пользуясь следующим достаточным условием.

Утверждение. Если для z” существует Допустимое решение заДачи  и z” е [Ч, ф], то z” — оптимальное значение целевой функции (2.1).

Доказательство. Достаточно показать, что размещение со значением целевой функции < z” не является допустимым.