Определение метрического пространства. Примеры. Пространство изолированных точек

Лекция 1.

Метрические пространства

В математике очень важную роль играет понятие пространства, т. е. множества, между элементами которого аксиоматически заданы некоторые соотношения. В таком случае говорят, что на множестве задана структура соответствующего пространства. В этой лекции мы рассмотрим понятие метрического пространства — множества, для элементов которого определено понятие расстояния. С помощью расстояния можно ввести одну из важнейших операций анализа — операцию предельного перехода.

1.1        Определение метрического пространства. Примеры

Определение 1.1. Метрическим пространством называется пара (X, ρ), где X — некоторое множество, а ρ: X × X → R₊ — функция расстояния (метрика), удовлетворяющая следующим аксиомам (аксиомам расстояния):

1.  для любых x, y ∈ X ρ(x, y) > 0, причем ρ(x, y) = 0 тогда и только тогда, когда x = y (неотрицательность);

2.  для любых x, y ∈ X ρ(x, y) = ρ(y, x) (симметричность);

3.  для любых x, y, z ∈ X ρ(x, z) 6 ρ(x, y) + ρ(y, z) (неравенствотреугольника).

В дальнейшем, мы зачастую метрическое пространство будем обозначать тем же символом, что и само множество X.

Приведем примеры метрических пространств.

1.  Пространство изолированных точек. Для произвольного множества X введем функцию расстояния следующим образом:

(

0, если x = y, ρ(x, y) =

                                                                                             1,      если x 6= y.

Введенная функция удовлетворяет аксиомам расстояния (показать самостоятельно).

2.  Пространство действительных чисел R. Расстояние вводится следующим образом:

                                                                                  ρ(x, y) = |x − y|.                                                       (1.1)

3.  Пространство — множество упорядоченных наборов из n вещественных чисел x = (x₁, ..., x_n), x_k ∈ R, k = 1, ..., n

с функцией расстояния

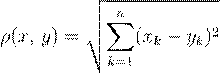                                                                     .                                           (1.2)

Неравенство треугольника вытекает из неравенства Коши—Буняковского (позже мы докажем неравенство Коши—Буняковского для более общего случая):

.

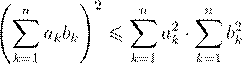Действительно,

 .

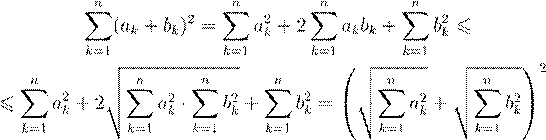Извлекая квадратный корень из обеих частей неравенства и заменяя a_k = x_k − y_k, b_k = y_k − z_k, получаем неравенство треугольника для метрики (1.2). Проверка остальных аксиом очевидна.

4.  Пространство. На множестве Rⁿ может быть введена метрика следующим образом:

.

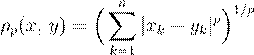Справедливость аксиом 1 и 2 очевидна. Справедливость аксиомы 3 следует из неравенства Минковского, справедливое при p > 1:

                                           ³Xn                               ´1/p             ³Xn                  ´1/p            ³Xn                 ´1/p

                                                           |a_k + b_k|^p 6               |a_k|^p              +             |b_k|^p           .

                                              k=1                                                       k=1                                         k=1

5.  Пространство C[a, b] непрерывных на отрезке [a, b] функций. Расстояние вводится следующим образом:

ρ(x, y) = max |x(t) − y(t)|

a6 t6 b

(выполнимость аксиом расстояния проверить самостоятельно). Это пространство играет очень важную роль в анализе.

1.2           Открытые и замкнутые множества. Плотные множества

Введем несколько понятий. Открытым шаром B(x₀, r) в метрическом пространстве X называется совокупность точек x ∈ X, удовлетворяющих условию ρ(x, x₀) < r. Замкнутым шаром B[x₀, r] называется совокупность точек x ∈ X, удовлетворяющих условию ρ(x, x₀) 6 r. Точка x₀ называется центром, а число r > 0 — радиусом шара. Открытый шар радиуса ε с центром в точке x₀ называется ε-окрестностью точки x₀ и обозначается как O_ε(x₀).

Приведем классификацию точек множества. Точка x ∈ X называется точкой прикосновения множества M ⊂ X, если любая ее окрестность содержит хотя бы одну точку из M. Точка x ∈ X называется предельной точкой множества M ⊂ X, если любая ее окрестность содержит бесконечно много точек из M. Точка x ∈ M называется внутренней точкой множества M, если существует окрестность O_ε(x), целиком лежащая в M. Точка x ∈ M называется изолированной точкой множество M, если