◄Из существования первого предела следует, что f(x)
![]() − k = β(x),
где β(
)x - бесконечно малая функция. Тогда x
− k = β(x),
где β(
)x - бесконечно малая функция. Тогда x
f (x) = kx + x⋅β(x). Отнимем от обеих частей величину kx и найдем предел при x →∞, lim( f (x) −kx)= limx⋅β(x). Из
x→∞ x→∞
lim( f (x) −kx)= b следует limx⋅β(x) = b. Поэтому
x→∞ x→∞ x⋅β(x) = b +α(x), где ( )α x - бесконечно малая функция. Следовательно, f (x) = kx + x⋅β(x) = kx + b +α(x).►
 ПРИМЕР. Найти асимптоты
графика функции y =
x(x-2). f (x)
ПРИМЕР. Найти асимптоты
графика функции y =
x(x-2). f (x)
Решение. Найдем последовательно пределы lim и
x→∞ x
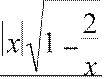 lim(
f (x) −kx).
Второй предел находится при условии, что первый
lim(
f (x) −kx).
Второй предел находится при условии, что первый
x→∞
![]()
![]()
![]() f(x)x(x-2)
f(x)x(x-2)
![]() из них конечен.
Тогда lim. x→∞ xxx
из них конечен.
Тогда lim. x→∞ xxx
Если x > 0, то модуль раскрываем со знаком плюс, и
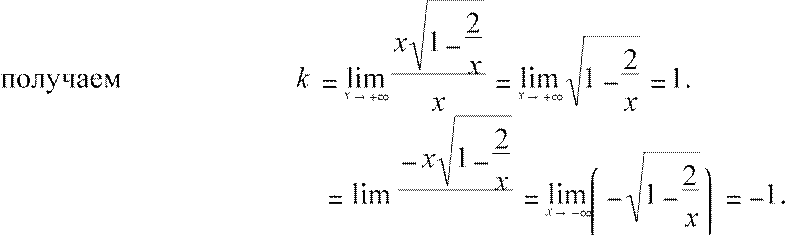 Если x < 0, то k
Если x < 0, то k
x→−∞ x
Найдем величину второго предела, домножив числитель и знаменатель (который равен единице) на сопряженное выражение:
x(x −2)− x2
![]() lim(
f (x)−kx)= lim(
x(x −2)
− x)= lim=
lim(
f (x)−kx)= lim(
x(x −2)
− x)= lim=
![]() x→+∞ x→+∞x→+∞ x(x
−2) + x
x→+∞ x→+∞x→+∞ x(x
−2) + x
−2x −2
![]()
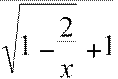 = lim= −1
= lim= −1
⎛ 2 ⎞ x→+∞
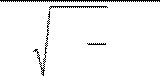 x⎜⎜⎝ 1− x +1⎟⎟⎠
x⎜⎜⎝ 1− x +1⎟⎟⎠
Таким образом, правая наклонная асимптота имеет вид y = x -1.
Аналогично рассматривается случай x →-∞.
x(x −2)− x2
= lim=
![]()
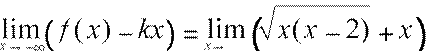 −∞ x→−∞ x(x
−2) − x
−∞ x→−∞ x(x
−2) − x
−2x 2
 lim= lim=1
lim= lim=1
x→+∞ ⎛ 2 ⎞ x→+∞
 − x⎜⎜⎝
1− x +1⎟⎟⎠
− x⎜⎜⎝
1− x +1⎟⎟⎠

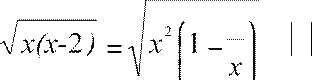 Тогда получим
левую наклонную асимптоту y =
-x +1. График
исходной функции со своими асимптотами представлен на рис. 12.
Тогда получим
левую наклонную асимптоту y =
-x +1. График
исходной функции со своими асимптотами представлен на рис. 12.
Значительно короче можно решить пример, используя «о»-малое.
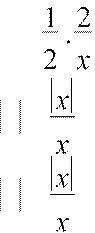
2 ⎛ 2⎞![]()
y = =
x ⋅⎜1− ![]() ⎟ .
⎟ .
⎝ x⎠
Поскольку x→∞, заменим скобку асимптотическим равенством. Получим
![]()
![]()
 ⎛
⎛ ![]() ⎛ ⎛1⎞⎞ x y = x ⋅⎜1−
⎛ ⎛1⎞⎞ x y = x ⋅⎜1− ![]() ⎟ = x⎜1− + o⎜
⎟ = x⎜1− + o⎜ ![]() ⎟⎟ = x − +o(1).
⎟⎟ = x − +o(1).
⎝ x⎠⎝⎝ x⎠⎠ x
Пусть x → +∞. Тогда y = x − +o(1) = x −1+o(1).
Пусть x→−∞. Тогда y = x − +o(1) = −x +1+o(1).
Как известно, о(1) есть бесконечно малая величина. Правая y = x-1 и левая y = -x +1 наклонные асимптоты получены.
Замечание 1. Прямая x = x0 не может быть вертикальной асимптотой, если функция непрерывна в точке x = x0 . Поэтому вертикальные асимптоты следует искать в точках разрыва функции.
Замечание 2. Горизонтальная асимптота является частным случаем наклонной при k=0.
Замечание 3. Если при нахождении горизонтальной асимптоты получается lim f (x) = ∞, то функция может иметь
x→∞
наклонную асимптоту.
Замечание 4. Кривая y=f(x) может пересекать свою асимптоту, причем многократно.
При построении графика функции необходимо провести ее предварительное исследование. Построение сразу по точкам, за исключением элементарных случаев, может привести к потере на графике важных свойств функции. Примерная схема исследования функции с целью построения ее графика представлена ниже.
1. Область определения D(y) и область допустимых значений
E(y) функции.
2. Симметрия и периодичность.
3. Точки разрыва и промежутки непрерывности функции.
4. Нули функции и промежутки постоянного знака.
5. Экстремумы и промежутки монотонности.
6. Точки перегиба и промежутки выпуклости.
7. Асимптоты.
Замечание 1. Схема представлена как примерная. Пункты исследования можно опускать, если они дают банальную информацию, или переставлять, если обнаруживаются интересные особенности поведения графика. Однако без нахождения разрывов, экстремумов, асимптот и исследования на выпуклость часто невозможно получить график, правильно отражающий поведение функции.
Замечание2. Для уточнения графика можно найти некоторые дополнительные точки, но иногда удается обойтись и без них.
Замечание 3. Рекомендуется строить график одновременно с исследованием функции, нанося на координатную плоскость информацию по завершении каждого пункта исследования.
ПРИМЕР 1. Провести полное исследование функции
1
![]() y = 2 и построить график.
y = 2 и построить график.
1+ x
1. Областью определения является вся числовая ось.
2. Функция четная: f(-x) = f(x), так что ее график симметричен относительно оси ординат. Из четности функции следует, что достаточно построить ее график в правой полуплоскости, а затем отразить его в левую полуплоскость.
3.
![]() Точек разрыва
нет, функция max непрерывная
на всей числовой оси. y′(
x ) + 4.
При х=0 имеем у=1. Функция положительна при всех
x, так что график Рис.
13 функции лежит в верхней полуплоскости.
Точек разрыва
нет, функция max непрерывная
на всей числовой оси. y′(
x ) + 4.
При х=0 имеем у=1. Функция положительна при всех
x, так что график Рис.
13 функции лежит в верхней полуплоскости.
2x
5.
![]() y′ = − 2 2 . Функция возрастает
при х<0 и убывает при (1+
x )
y′ = − 2 2 . Функция возрастает
при х<0 и убывает при (1+
x )
 х>0.
Точка х=0 — критическая. При переходе перегиб х через точку х=0 производная у'(х)
меняет y′′(
x ) - +
знак с плюса на минус (рис.13).
х>0.
Точка х=0 — критическая. При переходе перегиб х через точку х=0 производная у'(х)
меняет y′′(
x ) - +
знак с плюса на минус (рис.13).
Следовательно, точка х=0 — точка Рис. 14 максимума, у(0) = 1.
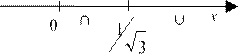
1-3x2
6.
![]() y′′ = -2 2 3 . Вторая
производная обращается в нуль в
y′′ = -2 2 3 . Вторая
производная обращается в нуль в
(1+ x )
 точках x =
±
точках x =
±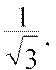 Исследуем точку x =
Исследуем точку x =
![]() . При
x
. При
x 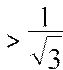 имеем
у" >0, т.е. кривая выпукла вниз; при
имеем
у" >0, т.е. кривая выпукла вниз; при
x
< ![]() получаем
у"<0 (кривая выпукла вверх) (рис.14). Следовательно, x =
получаем
у"<0 (кривая выпукла вверх) (рис.14). Следовательно, x = ![]() - точка
перегиба
- точка
перегиба
1
7. lim ![]() 2 = 0. График имеет горизонтальную асимптоту
у = 0, x→+∞1+ x
2 = 0. График имеет горизонтальную асимптоту
у = 0, x→+∞1+ x
наклонных асимптот нет.
Строим график в правой полуплоскости и симметрично отражаем его в левую полуплоскость. График функции изображен на рис. 15.
ПРИМЕР 2. Провести полное исследование функции
(x +1)3
y = ![]() 2 и построить график.
2 и построить график.
(x −1)
1.Область определения функции х≠1, т.е.D(y)=(-∞;1)∪(1;+∞).
Так как при х=-1 y<0, а при x>-1 y>0, и lim y(x) = −∞,lim y(x) = +∞, то множество значений функции
x→−∞ x→+∞
Е(у)=(-∞;+∞).
2.Функция у(х) не является периодической. Она ни четная, ни нечетная, т.е. ее график не обладает симметрией. (Этот очевидный для данной функции пункт можно было опустить).
3.В точке х=1 функция имеет разрыв y( x) - +
![]()
второго рода, -1 х
т.к. lim y(x) = +∞, lim y(x) = +∞. Рис. 16 x→1−0 x→1+0
4.Точки пересечения с осями координат: х=0, у=1, и х=-1,
у=0.Промежутки постоянного знака y′( x ) + - min + представлены на рис.
16. ![]()
5.Найдем интервалы возрастания, Рис. 17
убывания и экстремумы функции. Для этого вычислим первую производную:
![]() 3(x +1)2 (x −1)2 − 2(x −1)(x +1)3 (x +1)2 (x − 5) y′ = 4 = 3 .
3(x +1)2 (x −1)2 − 2(x −1)(x +1)3 (x +1)2 (x − 5) y′ = 4 = 3 .
(x −1) (x −1)
Отсюда получим а) у′>0 при x<1 и x>5, следовательно, на этих промежутках функция возрастает, а при х∈(1,5) у′<0 и функция убывает. (рис.
9.17).
б) у′=0 при х=5 и в точке (5;27/2) перегиб
y′′( x ) функция имеет локальный минимум. ![]() - + + х
- + + х
∩ -1 ∪ 1 ∪
Точка х=-1 тоже является критической Рис. 18.
точкой у(-1)=0, но локального экстремума функции в этой точке нет.
6. Найдем интервалы выпуклости функции. Для этого вычис24(x +1)
лим вторую производную: у′′ == ![]() 4 . Тогда у″<0
при х<-1 и (x −1)
4 . Тогда у″<0
при х<-1 и (x −1)
функция выпукла вверх, а на промежутках -1<x<1 и x>1 у″>0 и функция
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.