Ульяновский государственный технический университет
Институт авиационных технологий и управления
,
Сборник лабораторных работ по курсу высшей математики
ОГЛАВЛЕНИЕ
ВВЕДЕНИЕ.. 4
1. РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ.. 5
1.1. Общая характеристика методов решения систем линейных уравнений. 5
1.2. Решение систем с помощью обратной матрицы. Формулы Крамера. 6
1.3. Метод Гаусса. 7
1.4. Задания для выполнения лабораторной работы.. 8
2. ПРИБЛИЖЕНИЕ ФУНКЦИЙ. 9
2.1. Постановка задачи интерполирования. 9
2.2. Интерполяционная формула Лагранжа. 10
2.3. Интерполяционный полином Ньютона. Тригонометрическое интерполирование. 11
2.4. Задания для выполнения лабораторной работы.. 12
3. ПРИБЛИЖЕННОЕ ИНТЕГРИРОВАНИЕ ФУНКЦИЙ.. 13
3.1. Квадратурные формулы.. 13
3.2. Формула Симпсона. 15
3.3. Метод Монте-Карло. 16
3.4. Задания для выполнения лабораторной работы.. 17
4. ПРИБЛИЖЕННОЕ РЕШЕНИЕ АЛГЕБРАИЧЕСКИХ И ТРАНСЦЕНДЕНТНЫХ УРАВНЕНИЙ 18
4.1. Отделение корней уравнения. 18
4.2. Метод хорд и метод касательных. 19
4.3. Метод итераций. 20
4.4. Задания для выполнения лабораторной работы.. 22
5. ЗАДАЧА КОШИ ДЛЯ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ.. 23
5.1. Метод Эйлера. 23
5.2. Метод Рунге-Кутта. 25
5.3. Задания для выполнения лабораторной работы.. 26
6. РЕШЕНИЕ ПЕРВОЙ КРАЕВОЙ ЗАДАЧИ ДЛЯ УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ МЕТОДОМ КОНЕЧНЫХ РАЗНОСТЕЙ.. 27
6.1. Постановка задачи. 27
6.2. Задания для выполнения лабораторной работы.. 29
7. УРАВНЕНИЕ РЕГРЕССИИ И КОЭФФИЦИЕНТ КОРРЕЛЯЦИИ.. 30
7.1. Уравнение регрессии. 30
7.2. Коэффициент корреляции. 31
7.3. Задания для выполнения лабораторной работы.. 32
ПРИЛОЖЕНИЯ..............................................................................................................................................................33
БИБЛИОГРАФИЧЕСКИЙ
СПИСОК……………………………………………………………………………...52
ВВЕДЕНИЕ
Общим подходом для всех численных методов является сведение математической задачи к конечно-мерной. Это чаще всего достигается дискретизацией исходной задачи, т. е. переходом от непрерывного аргумента к дискретному. После дискретизации необходимо построить вычислительный алгоритм, т. е. указать конечную последовательность арифметических и логических действий при решении задачи на ЭВМ. Полученное решение дискретной задачи принимается за приближенное решение исходной задачи.
Математическая постановка любой задачи уже содержит некоторую неточность в связи с двумя обстоятельствами:
1. Математическая модель реального объекта никогда не учитывает всех явлений, влияющих на состояние этого объекта;
2. В уравнения математической модели входят некоторые задаваемые параметры, значения которых получаются в результате измерений различных характеристик моделируемого объекта. Всякое измерение производится с ошибкой.
В этой связи, только лишь записав в математической форме научно-технические задачи, уже появляется некоторая погрешность, которая является неустранимой.
Сформулировав математическую задачу, необходимо искать метод ее решения, и часто этот метод бывает приближенным. Это означает, что в результате применения метода могут быть получены не точные, а приближенные значения искомой функции, даже если все вычисления проделаны абсолютно точно. При создании численных методов закладывается возможность отслеживания таких погрешностей и доведения их до сколь угодно малого уровня. Отсюда погрешности метода считаются устранимыми.
Любые арифметические операции производятся над числами, усеченными до определенного количества разрядов. Вследствие этого неизбежно происходит округление как исходных численных данных, так и результатов. Вычислительный алгоритм называется устойчивым, если в процессе его работы вычислительные погрешности возрастают незначительно.
Все три описанных типа погрешностей – погрешности задачи, погрешности метода, погрешности округлений – в сумме дают полную погрешность результата решений задачи. При выводе оценок погрешностей численных методов обычно исходят из предположения, что все операции над числами выполняются точно. Это означает, что погрешность округлений не должна существенно отражаться на результатах реализации методов.
Разность между приближенным значением величины ![]() и ее точным значением
и ее точным значением ![]()
![]() называется
абсолютной погрешностью приближенного числа
называется
абсолютной погрешностью приближенного числа ![]() .
Под оценкой погрешности приближенной величины понимают неравенство вида
.
Под оценкой погрешности приближенной величины понимают неравенство вида ![]() , где (
, где (![]() )
)
![]() – граница абсолютной погрешности.
– граница абсолютной погрешности.
К решению систем линейных алгебраических уравнений сводится большое количество задач не только алгебры, но и уравнений математической физики, математического анализа, операционные методы.
Пусть имеется система n линейных уравнений:
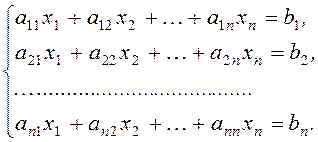 (1.1)
(1.1)
В матричной форме она имеет вид:
A .X = B, (1.2)
где A – матрица коэффициентов, В – столбец свободных членов, X – столбец неизвестных:
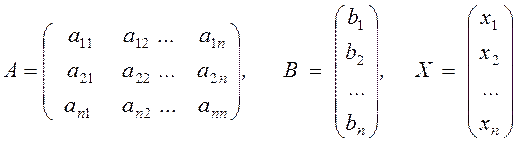 .
.
Наличие решений системы (1.1) определяется
соотношением рангов матрицы системы (A) и расширенной матрицы системы (![]() ). (Расширенная матрица – матрица,
содержащая коэффициенты при неизвестных и коэффициенты справа от знака равенства
в уравнениях (столбец свободных членов)). Если ранг матрицы A не
равен рангу расширенной матрицы
). (Расширенная матрица – матрица,
содержащая коэффициенты при неизвестных и коэффициенты справа от знака равенства
в уравнениях (столбец свободных членов)). Если ранг матрицы A не
равен рангу расширенной матрицы ![]() , то
система не имеет решений. Если ранги матриц равны, возможны два случая:
, то
система не имеет решений. Если ранги матриц равны, возможны два случая:
- если ранг меньше количества неизвестных, то система имеет бесконечное множество решений;
- если ранг матрицы A равен количеству неизвестных, то система
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.