Понятие вариации и показатели вариации. Абсолютные показатели вариации. Среднее линейное отклонение

МОДУЛЬ 2

2.1. ПОНЯТИЕ ВАРИАЦИИ И ПОКАЗАТЕЛИ ВАРИАЦИИ

Понятие вариационного ряда распределения. Виды вариационных рядов. Классификация показателей. Абсолютные и относительные показатели размера вариации.

Вариация – _______________________________________________________

_____________________________________________________________________

Меры вариации

 

абсолютные                                                    относительные

__________________________             _________________________________

__________________________             _________________________________

__________________________             _________________________________

__________________________             _________________________________

Абсолютные показатели вариации

Размах вариации  – __________________________________

_____________________________________________________________________

Среднее линейное отклонение – ____________________________________

_____________________________________________________________________

простое 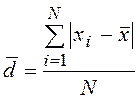                  взвешенное .

Дисперсия – ______________________________________________________

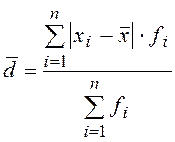простая 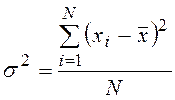                 взвешенная .

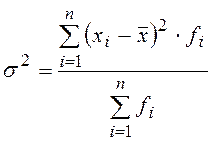Среднее квадратическое отклонение – ______________________________

_____________________________________________________________________

простое 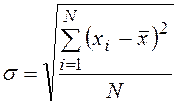                 взвешенное .

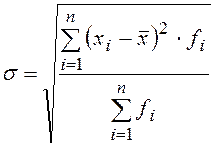Если распределение близко к нормальному, то . Тогда для нормального распределения справедливо «правило трех сигм»: в  находятся 68,3 % количества наблюдений, в  находятся 95,4 % количества наблюдений, в  находятся 99,7 % количества наблюдений.

Относительные показатели вариации

Коэффициент осцилляции –  _______________________________________

_____________________________________________________________________

.

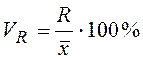Линейный коэффициент вариации – ________________________________

_____________________________________________________________________

.

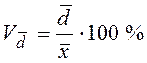Коэффициент вариации – __________________________________________

_____________________________________________________________________

.

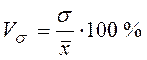Совокупность считается однородной, если .

Вариация альтернативного признака

Вариация альтернативного признака – ______________________________

_____________________________________________________________________

 – варианты значений признака. Пусть  – доля тех единиц совокупности, для которых ,  для . Известно, что , тогда

,                ,

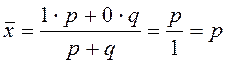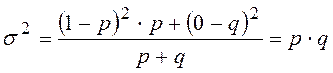 при p=0,5.

Обобщенной характеристикой различий внутри вариационного ряда служит энтропия распределения (мера неопределенности данных наблюдения). Показатель энтропии 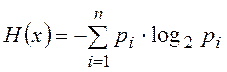. Если все варианты равновероятны, то  – максимальное значение энтропии для равновероятных вариант. Если все варианты (кроме одного) равны 0, то .

Для альтернативного признака:  (бит).

Пример:

Сорт	1–й	2–й	3–й	Брак	Итого
Вероятность	0,9	0,04	0,05	0,01	1

Решение.

(бит)

Энтропия распределения интерпретируется как мера __________________

_______________________________________________________________________________________________________________________________________________________________________________________________________________

Относительная энтропия определяется как 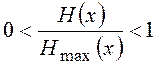.  Чем меньше относительная энтропия, тем меньше неопределенность, тем выше однородность совокупности.

2.2. ВИДЫ ДИСПЕРСИЙ И ПРАВИЛО ИХ СЛОЖЕНИЯ

Межгрупповая и внутригрупповая, общая дисперсии. Правило сложения дисперсий. Дисперсия доли признака. Правило сложения дисперсий для доли признака. Коэффициент детерминации и эмпирическое корреляционное отношение, их экономическая интерпретация.

Свойства дисперсии

1. ;	3. ;
2. ;	4. .

Формула, применяемая при вычислении дисперсии: .

Вычисление дисперсии по способу моментов (применяется для вариационных рядов с равными интервалами): 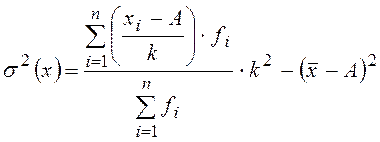, где  – ширина интервала,  – условный нуль, в качестве которого удобно использовать середину интервала, обладающего наибольшей частотой (мода).

Виды дисперсий и правило их сложения

Значение признака x	Число единиц в j–той группе				Итого
	1	2	…
			…
			…
…	…	…	…	…	…
			…
Итого			…

Рассчитаем  штук частных средних, т.е. среднее значение признака в каждой группе:

,   ,  . . .  , .

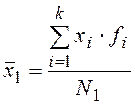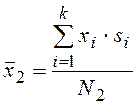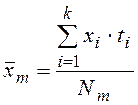Теперь можем рассчитать общую среднюю:

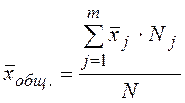, где ,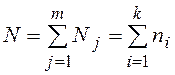

Тогда общая дисперсия 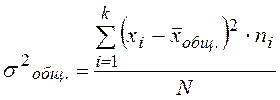 измеряет вариацию __

____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

Межгрупповая дисперсия 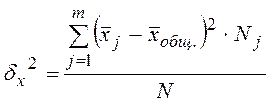 , где  – групповые средние и  – численности по группам.

Межгрупповая дисперсия как отклонение групповой средней от общей средней характеризует ________________________________________________

_______________________________________________________________________________________________________________________________________________________________________________________________________________

Рассчитаем значения дисперсий в каждой группе – (частных) групповых дисперсий:

,  ,  …  ,

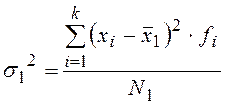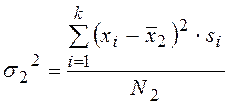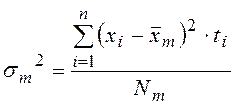
или по общей формуле  ,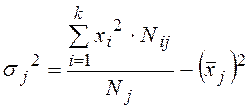

где  – частоты при  в каждой j–той группе.

Теперь можем рассчитать значение внутригрупповой дисперсии: 

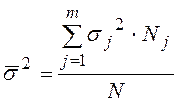, которая представляет собой ____________________________________________

____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

Общая дисперсия равна сумме средней из внутригрупповых и межгрупповой дисперсий:

 – правило сложения дисперсий.

Эмпирический коэффициент детерминации 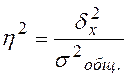 позволяет найти

____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

Эмпирическое корреляционное отношение 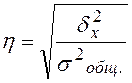  характеризует

_______________________________________________________________________________________________________________________________________________________________________________________________________________

	Связь		Связь
0	Отсутствует	0,5 – 0,7	Заметная
0 – 0,2	Очень слабая	0,7 – 0,9	Тесная
0,2 – 0,3	Слабая	0,9 – 0,99	Весьма тесная
0,3 – 0,5	Умеренная	1	Функциональная

Итак, , тогда
при	при
группировочный признак не влияет на вариацию значений результативного	результативный признак меняется только в зависимости от группировочного, влияние прочих факторных признаков равно 0.

Дисперсии доли для альтернативного признака

 – варианты значений признака в каждой группе статистической совокупности. Пусть  – доля тех единиц совокупности в –той группе, для которых ,  – доля тех единиц –той группы совокупности, для которых . Известно, что , тогда внутригрупповая дисперсия доли:

,

Средняя из внутригрупповых дисперсий 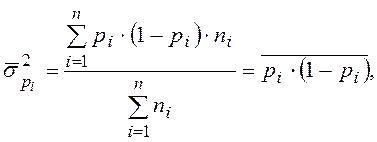 где  – численность единиц в отдельных группах совокупности.

Межгрупповая дисперсия доли 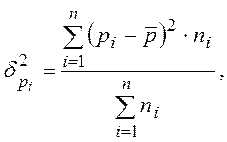 где 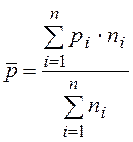 – доля изучаемого признака во всей совокупности.

Общая дисперсия:  или  – теорема сложения дисперсий доли признака.

2.3. МОМЕНТЫ РАСПРЕДЕЛЕНИЯ. ПОКАЗАТЕЛИ ФОРМЫ РАСПРЕДЕЛЕНИЯ

Структурные характеристики вариационного ряда. Графический способ нахождения моды и медианы. Показатели дифференциации и концентрации. Моменты распределения. Способы расчета моментов. Показатели формы распределения – асимметрия и эксцесс, их графическая иллюстрация.

Средние структурные

Мода  дискретного распределения  – такое спектральное значение , что предшествующее и последующее за ним спектральные значения имеют вероятности, меньшие, чем  – это наиболее часто встречающееся значение  признака у единиц совокупности.

.

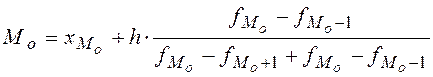Мода может быть найдена графически с помощью гистограммы.

Медиана распределения  – то значение признака, которое делит единицы ранжированного ряда пополам. 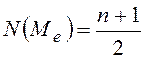, если  – четное, то медиана лежит между значениями ранжированного признака, если  – нечетное, то  совпадает точно с одним из значений признака.

.

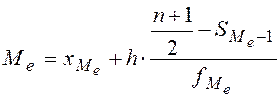Медиана может быть найдена с помощью кумуляты.

Если в качестве показателя центра распределения используется медиана, то для характеристики вариации признака в совокупности используется квартильное отклонени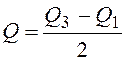е , где  – соответственно первая и третья квартили распределения.  также можно использовать вместо размаха вариации, чтобы избежать недостатков, связанных с использованием крайних значений.

Квартили – ______________________________________________________

_________________________________________, выбранные таким образом, что 25% единиц совокупности будут меньше по величине ; 25% единиц будут заключены между и ; 25% – между  и остальные 25% превосходят .

Расчетные формулы: ;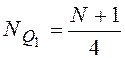       

;             ;

;       

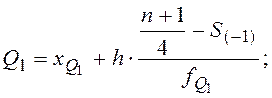
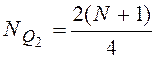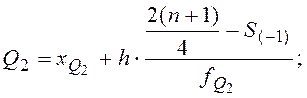
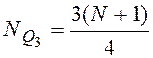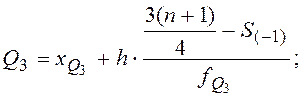
В симметричных и умеренно симметричных распределениях 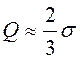 . Квартильное отклонение вычисляют в тех случаях, когда  найти трудно или невозможно. Если 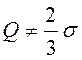, то распределение несимметричное.

Относительный показатель квартильной вариации: .

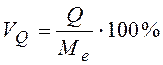Анализ вариации в рядах распределения полезно дополнить показателями дифференциации:

1)  Коэффициент фондовой дифференциации: 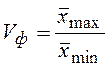, где  – среднее из 10% наибольших значений признака,  – среднее из 10% наименьших значений признака;

2)  Коэффициент децильной дифференциации: 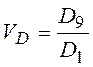, где  – девятая дециль,  – первая дециль.

Расчетные формулы для децилей при предположении равномерного наращивания величины интервала на каждую единицу частоты:

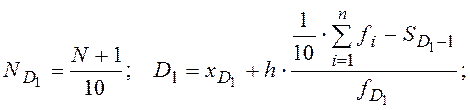
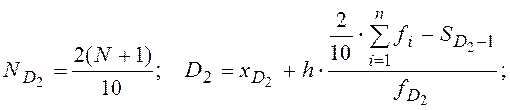
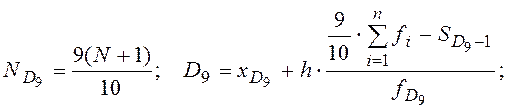
Децили

                                                                            

Моментом распределения называется _______________________________

__________________________________________________________________________________________________________________________________________

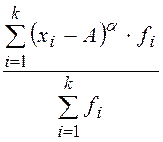, где  – порядок момента,  – величина, от которой определяются отклонения