Формула полной вероятности. Формула Байеса. Схема испытаний Бернулли. Случайные величины, страница 5

Функция распределения случайной величины и её свойства

Ряд распределения можно построить только для дискретной случайной величины, для непрерывной нельзя даже перечислить все её возможные значения. Универсальным способом задания закона распределения для любых случайных величин служит функция распределения.  Функцией распределения (или интегральной функцией распределения) F x( )случайной величины Х называется функция, которая для любого действительного значения xравна вероятности события {X < x}, т.е. 

                       F x( ) = P X( < x ,) x∈ −∞ +∞(                   ,       ).                                         (4)

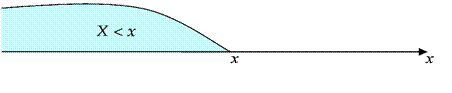
Геометрически равенство (4) можно истолковать так: F x( ) − это вероятность того, что с.в.

Х примет значение, которое на числовой оси изображается точкой, лежащей левее точки x, т.е. случайная точка Х попадёт в интервал (−∞,x) :

        

Свойства функции распределения (без доказательства):

1.  0 ≤ F x( ) ≤ 1, т.к. это вероятность.

2.  F(−∞ ≡)       lim F x( ) = 0, т.к. F(−∞) = _{P X}(   < −∞) = P V( ) = 0 , где V – невозможное

x→−∞ событие.

3.  F(+∞ ≡)       lim F x( ) = 1 т.к. F(+∞) = _{P X}(    < +∞) = P U( ) = 1, где U – достоверное

x→+∞ событие.

4.  P a( ≤ X < b) = F b( ) − F a( )                                                            (5)

5.  F x( ) − неубывающая функция, т.е., если x₁ < x₂ , то  F x( 1) ≤ F x( 2) .

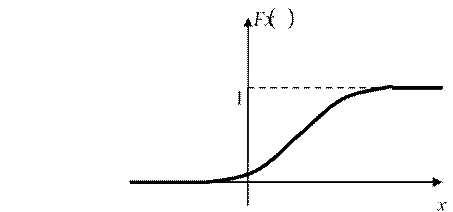
 Функция распределения непрерывной случайной величины непрерывна , её график имеет вид:

Функция распределения дискретной случайной величины

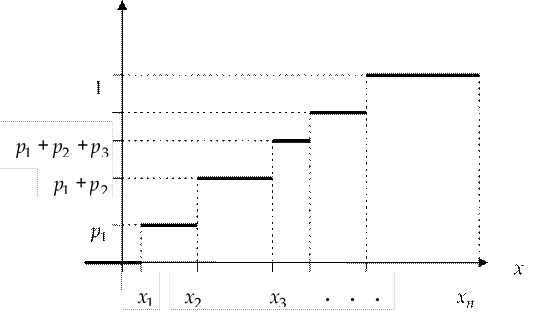
Вычислим функцию распределения д.с.в. Х, имеющей ряд распределения 

xk	x1	x2	.  .  .	xn
pk	p1	p2	.  .  .	pn

Будем задавать различные значения x и находить для них F x( ) = P X( < x) .

Пусть x₁ < x₂ < ...< x_n .

•  Если x ≤ x₁, то событие {X < x} невозможное, т.к. у с.в. нет значений, меньших x, следовательно, F x( ) = 0.

•  Если x₁ < x ≤ x₂, то событие {X < x}={X = x₁}, P X(       < x) = P X(  = x₁) = p₁.

•  Если x₂ < x ≤ x₃, то событие {X < x}⁼{X = x₁}⁺{X = x₂}, причём события в правой части равенства несовместны. P X( < x) = P X( = x₁) + P X( = x₂) = p₁ + p₂ .

•  Действуя аналогично для каждого следующего промежутка, наконец, получим,  что если x > x_n , то событие {X < x}⁼{X = x₁}⁺{X = x₂}+ ...⁺{X = x_n}, причём собы-

               тия в правой части равенства несовместны. P X(  < x) == p₁ + p₂ + ...+ p_n = 1.

Окончательно получили:

                               0,                         x ≤ x ;₁



                              _p ,₁                           x₁ < x ≤ x ;₂

                             p₁ + p ,₂            x₂ < x ≤ x ;₃

              F x( ) =                                                                                              (5)

                               p₁ + p₂ + p , x_{3 3} < x ≤ x ;₄

^⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅



                             1,                        x > ^{x .}_n

График этой функции имеет вид:

                   F x( )

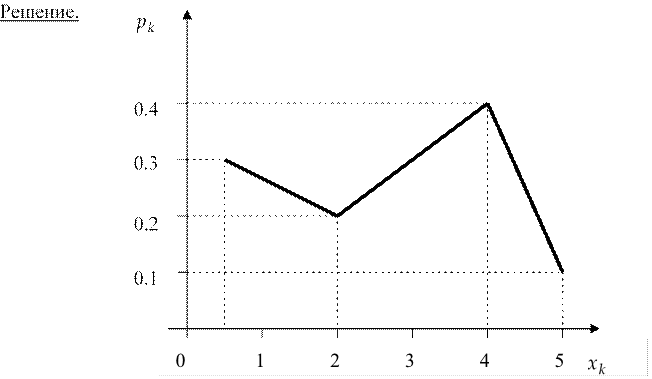
Пример 4. Дан ряд распределения с.в. Х:

xk	-2.4	3.1	5.2
pk	0.3	0.1	0.6

Найти функцию распределения.

Решение.
0, 0 3. ,  F x( ) =  0 4. , 1,	при при при при	x ≤ −2 4. − 2 4. < x ≤ 3 1. 3 1. < x ≤ 5 2. x > 5 2. .