Электрические цепи синусоидального тока. Основные сведения. Гармоническое воздействие, страница 2

.                                                                                (2.10)

Если (при известных I_m, ω и ψ_i) подставить в (2.10) значения напряжений на элементах цепи (2.7)…(2.9), то после соответствующих преобразований вычисляются амплитуда U_m и начальная фаза ψ_u, действующего на входе ЭЦ напряжения u(t) = U_m sin(ωt + ψ_u). Приведенный пример показывает, что использование временных функций при расчете даже простейших ЭЦ может вызвать определенные трудности вычислительного характера.

Наиболее просто задачи анализа синусоидальных ЭЦ решаются комплексным методом. Пусть комплексная амплитуда тока в цепи, приведенной на рис. 2.3, равна , тогда комплексы напряжений на элементах цепи в соответствии с выражениями  (2.7 – 2.9) имеют вид:

;                                                                  (2.11)

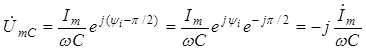;                 (2.12)

,                 (2.13)

Сумме синусоидальных напряжений (2.10) соответствует сумма комплексных амплитуд:

.           (2.14)

Соотношение (2.14) представляет собой уравнение по второму закону Кирхгофа, записанное в комплексной или векторной форме. Векторная диаграмма для ЭЦ представлена на рис. 2.4. Напряжение u_R совпадает по фазе с током i, поэтому вектор направлен одинаково с вектором . Поскольку напряжение u_C отстает, а напряжение u_L опережает по фазе ток i на π/2, то  вектор  сдвинут относительно вектора на угол π/2 «назад» (по часовой стрелке), а вектор  - 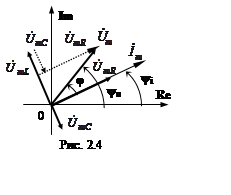«вперед» (против часовой стрелки). Сложив векторы  ,  и , получаем суммарный вектор входного напряжения , длина которого (U_m) определяет амплитуду входного напряжения цепи, а аргумент (ψ_u) – начальную фазу этого напряжения.. Из рис. 2.4 следует, что векторсдвинут против часовой стрелки относительно вектора на угол φ = ψ_u – ψ_i, т.е. напряжение u(t) опережает ток i(t) по фазе на угол φ. На векторной диаграмме угол φ отсчитывается в направлении от вектора к вектору .

Векторная диаграмма дает наглядное представление о процессах в электрической цепи, но точность графического построения невелика. Поэтому расчет ЭЦ лучше проводить, используя комплексные числа.

Входное комплексное сопротивление последовательного контура (рис. 2.3, а) определяется выражением

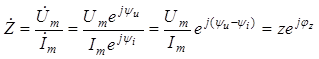,                             (2.15)

где z = U_m/I_m – полное сопротивление последовательного контура, а аргумент комплексного сопротивления φ_z = ψ_u – ψ_i.

Подставив в (2.15) значение комплексной амплитуды (2.14) с учетом выражений (2.11)…(2.13) получим

.     (2.16)

Действительная часть комплексного сопротивления r называется активным сопротивлением, а мнимая часть x = x_L – x_C – реактивным сопротивлением цепи. Из (2.15) и (2.16) следует, что

.    (2.17)

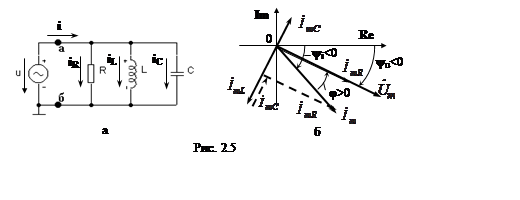
На рис. 2.6, а изображена электрическая цепь, состоящая из трех параллельно соединенных пассивных элементов R, L и C (параллельный контур), к которой приложено синусоидальное напряжение u(t) = U_m sin(ωt +ψ_u). Определим токи в ветвях параллельного контура, используя комплексный метод расчета. По первому закону Кирхгофа для комплексных амплитуд токов

                                                                         (2.18)

Введя обозначение комплексной амплитуды напряжения , приложенного к параллельно соединенным элементам ЭЦ, и применив для каждой ветви закон Ома в комплексной форме, получим

;                                           (2.19)

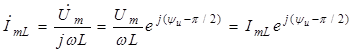;                    (2.20)

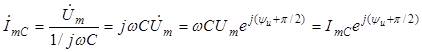.   (2.21)

Из полученных выражений следует, что ток в сопротивлении совпадает по фазе с приложенным напряжением: ψ_iR = ψ_u, ток в индуктивности отстает по фазе от напряжения на угол π/2: ψ_iL = ψ_u – π/2, а ток в емкости опережает напряжение на угол π/2: ψ_iC = ψ_u + π/2. Векторная диаграмма напряжения и токов в ЭЦ показана на рис. 2.5, б.

Комплексной проводимостью ЭЦ (рис. 2.5) называется отношение комплексного тока к комплексному напряжению:

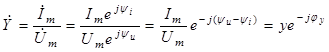.                          (2.22)