1.7 Решение системы канонических уравнений
Подставим найденные значения единичных и грузовых реакций в систему канонических уравнений (1):
0,400641 EJ ∙ Z1 + 0 ∙ Z2 – 0,027737 EJ ∙ Z3 + 384,0 = 0;
0 ∙ Z1 + 1,1875EJ ∙ Z2 – 0,260417 EJ ∙ Z3 + 85,33 = 0; (2)
– 0,027737 EJ ∙ Z1 – 0,260417 EJ ∙ Z2 + 0,113841 EJ ∙ Z3 + 0 = 0.
Решив полученную систему, найдем неизвестные перемещения
Z1 = – 1015,68
(кН
∙ м2); Z2 = –
253,09(кН ∙ м2);
Z3 = – 826,43 (кН
∙ м3).
Заметим, что Z1, Z2 являются углами поворота, Z3 – линейным горизонтальным перемещением. Знак "–" указывает, что их направления противоположны выбранным в п. 1.2 при образовании основной системы.
1.8 Построение окончательной эпюры изгибающих моментов М
Для построения окончательной эпюры изгибающих моментов необходимо сложить эпюры от действия каждого из перемещений Z1, Z2, Z3 и грузовую эпюру:
. (3)
Здесь М1, М2, М3 – эпюры изгибающих моментов от действительных перемещений узлов рамы (рисунок 13, а, б, в), они получаются умножением построенных ранее единичных эпюр (рисунки 4, 5, 6, б) на соответствующие значения перемещений Z1, Z2, Z3; Мр – эпюра от воздействия внешней нагрузки (рисунок 13, г).
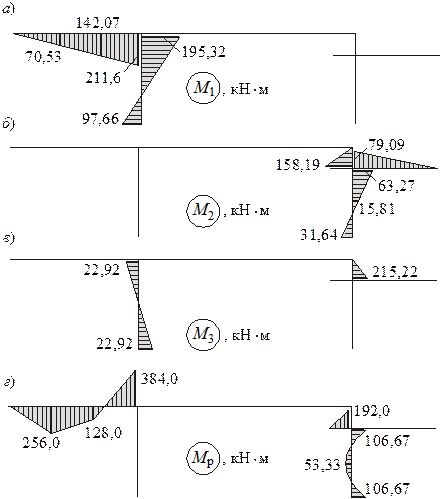
Рисунок 13
Складывая ординаты эпюр в соответствии с формулой (3), получаем окончательную эпюру изгибающих моментов (рисунок 14).
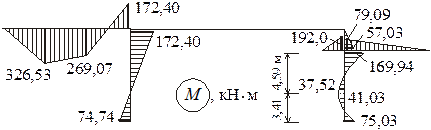
Рисунок 14
1.9 Проверка эпюры М
Статическая проверка
а) Проверка равновесия узлов
Вырезаем жесткие узлы рамы и рассматриваем их равновесие,
|
Рисунок 15 |
составляя уравнение Σ М узла = 0. Для первого узла (рисунок 15, а) 172, 40 – 172, 40 = 0. Для второго узла (рисунок 15, б) 57,03 + 192,00 – 169,94 – 79,09 = 0. Проверка выполняется. |
б) Проверка ординат
Для участков, загруженных в пролете внешней нагрузкой, должны выполняться условия равенства сумм характерных ординат и их дополнений соответствующим балочным ординатам.
Выполняем проверку ординат. Для участков с двумя сосредоточенными силами и распределенной нагрузкой выбираем соответствующие балки (рисунок 16, а, б), имеющие тот же пролет и схему нагружения. Определив опорные реакции, строим балочные эпюры моментов Мб. (Расчеты по построению Мб не приводим ввиду их простоты). Ниже изображаем эпюры изгибающих моментов для рассматриваемых участков, взятые из окончательной эпюры М (см. рисунок 14).
Соединяем крайние ординаты эпюр М прямыми линиями и находим из подобия треугольников дополнительные ординаты (на рисунке 16 они показаны пунктиром):
m1 =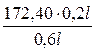 
= 57,47 кН ∙ м; m2 = 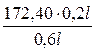= 114,93 кН ∙ м;
m3 = 75,03 + 
= 122,48 кН ∙ м.
Вычисляем суммы ординат эпюр М и соответствующих дополнений, сравниваем их с ординатами Мб. Для первой эпюры
m1 + 326,53 = 57,47 + 326,53 = 384 кН ∙ м;
m2 + 269,07 = 114,93 + 269,07 = 384 кН ∙ м;
Для второй эпюры
m3 + 37,52 = 122,48 + 37,52 = 160 кН ∙ м.
Полученные значения совпадают с соответствующими характерными ординатами балочной эпюры моментов, проверка выполняется.
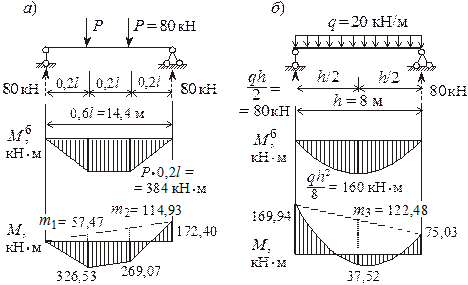
Рисунок 16
Деформационная проверка
Чтобы окончательно убедиться в правильности построения эпюры М, выполняем деформационную проверку. Она проводится так же, как и при расчете рам методом сил: вычисляется условное суммарное перемещение Dsp* перемножением окончательной эпюры М и суммарной единичной эпюры метода сил. Значение Dsp* должно равняться нулю:
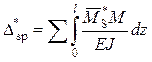= 0.
Здесь 
–
суммарная единичная эпюра изгибающих моментов, построенная для основной системы
метода сил.
Вычисляем степень
статической неопределимости заданной системы (см. рисунок 1) по формуле s = 3К – Ш = 3 ∙ 3 – 5 =
4. Формируем основную систему метода сил, вводя четыре шарнира и компенсируя их
четырьмя реакциями Х1, Х2, Х3,
Х4. Далее рассматриваем суммарное воздействие на основную
систему единичных сил Х1 = 1, Х2 = 1, Х3
= 1, Х4 = 1 (рисунок 17, а) и строим эпюру (рисунок 17, б).
Замечание. При построении данной эпюры удобно разбивать раму на однопролетные балки рассматривать их отдельно, прикладывая к каждой действующую нагрузку и реакции вышерасположенных балок.
|
а) |
|
|
б) |
|
Рисунок 17
Вычисляем Dsp*:
Dsp* =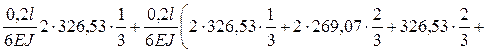 
.
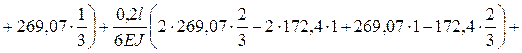
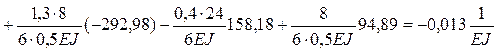Полученная величина Dsp*
0, деформационная
проверка выполняется, следовательно, окончательная эпюра изгибающих моментов М
построена верно.
1.10 Построение эпюр Q и N
Эпюра поперечных сил
Эпюра поперечных сил Q строится по готовой эпюре изгибающих моментов М. Для удобства вычислений отметим на оси рамы характерные точки (рисунок 18).
|
Рисунок 18 |
Для определения значений поперечных сил на участках, где эпюра М прямолинейна, используем дифференциальную зависимость
|
Здесь поперечная сила Qравна тангенсу угла наклона эпюры М. Правило знаков: сила Q считается положительной, если для совмещения оси стержня с эпюрой М ось вращают по часовой стрелке.
Длины участков: 0,2l = 0,2 ∙ 24 = 4,8 м; 0,4l = 0,4 ∙ 24 = 9,6 м;
h = 8 м; 1,3h = 1,3 ∙ 8 = 10,4 м; 0,3h = 0,3 ∙ 8 = 2,4 м; а = 2,4 м.
Участок 0-1: Q0–1 = 326,53/4,8 = 68,03 кН;
участок 1-2: Q1–2 = – (326,53 – 269,07)/4,8 = – 11,97 кН;
участок 2-3: Q2–3 = – (269,07 + 172,4)/4,8 = – 91,97 кН;
участок 4-5: Q4–5 = (172,4 +74,74)/10,4 = 23,76 кН;
участок 6-7: Q6–7 = – 57,03/2,4 = – 23,76 кН;
участок 8-9: Q8–9 = 79,09/9,6 = 8,24 кН;
участок 12-13: Q12–13 = – 192/2,4 = – 80 кН.
На участке 10-11,
где действует равномерно распределенная нагрузка, поперечную силу определяем с
помощью балочной аналогии. Представим этот стержень отдельно, как балку на двух
опорах. Приложим к его концам возникающие в системе внутренние моменты, взятые
из эпюры М (рисунок 19). Определим опорные реакции Y10, Y11 полученной
балки из уравнений 
; 
.
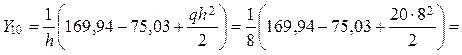91,86
кН;
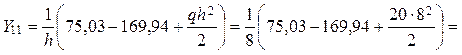68,14
кН.
Проверка: 
; 
.
|
Далее вычисляем поперечные силы в точках 10 и 11
Полученные значения откладываем на эпюре Q и соединяем прямой линией (рисунок 20). Подсчитаем абсциссу точки 14, в которой поперечная сила Q14 = 0, а, следо- |
|
вательно, М экстремален. Для этого определим Q14 и приравняем ее нулю:
= 0, отсюда 
м.
Изгибающий момент в точке 14 равен
М = – 169,94 – 
+
Y10z0 = – 169,94 – 20 ∙ 4,592/2 + 91,86 ∙ 4,59 =
= 41,03 кН ∙ м (растянуты левые волокна).
Отмечаем полученное значение на эпюре изгибающих моментов (см. рисунок 14).
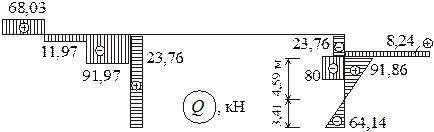
Рисунок 20
Эпюра продольных сил
Эпюру продольных сил N строим по готовой эпюре Q.
Вначале определим значение N на участке 0-3. Мысленно проведем сечение, отбросим правую часть и рассмотрим равновесие левой (рисунок 21, а). Очевидно, что N0–3 = 0.
Рассмотрим равновесие жестких узлов рамы 3-4, 6, 7-8-10-12. Приложим к ним поперечные и продольные силы в каждой из точек (рисунок 21, б, в, г). При этом поперечные силы покажем с их действительными направлениями (с учетом знака), а численное значение возьмем из эпюры Q.
Составим уравнения равновесия узлов.
Узел 3-4 (рисунок 21, б).
;
кН; 
;
кН.
Узел 6 (рисунок 21, в). Очевидно,
что 
;
;
кН (значение совпало с вычисленным
ранее).
Узел 7-8-10-13 (рисунок 21, г).
;
кН;
;
кН.
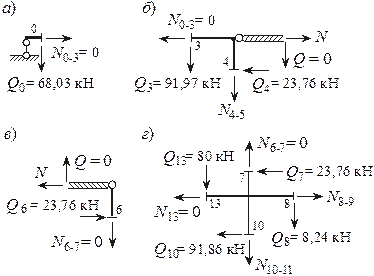
Рисунок 21
По полученным данным строим эпюру N (рисунок 22).
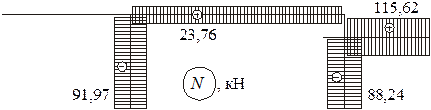
Рисунок 22
1.11 Статическая проверка равновесия всей рамы
Отсечем раму от опор, в местах полученных сечений приложим внутренние силы и моменты, взятые из эпюр М, Q, N (рисунок 23).
Составим уравнения равновесия рамы.
Суммы проекций всех сил на горизонтальную и вертикальную оси:
; – 23,76 + 68,14 + 115,62 – qh = 160 – 20 ∙ 8 = 0;
;
68,03 + 91,97
+ 88,24 – 8,24 – 3P = 240 – 3 ∙ 80 = 0.
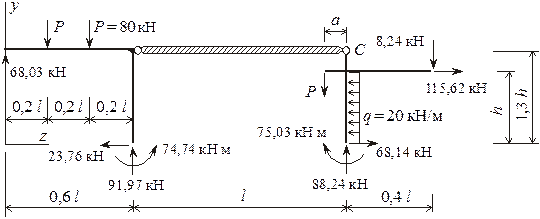
Рисунок 23
Сумма моментов всех сил относительно шарнира С:
;
– 68,03 ∙ 1,6l + P ∙ 1,4l + P ∙ 1,2l – 91,97 ∙ l – 23,76 ∙ 1,3h + 74,74 +
+ P ∙ a – qh(h/2 +0,3h) + 68,14 ∙ 1,3h – 75,03 – 8,24 ∙ 0,4l +
+ 115,62 ∙ 0,3h = – 68,03 ∙ 1,6 ∙ 24 + 80 ∙ 1,4 ∙ 24 + 80 ∙ 1,2 ∙ 24 –
– 91,97 ∙ 24 – 23,76 ∙ 1,3 ∙ 8 + 74,74 + 80 ∙ 2,4 – 20 ∙ 8 ∙ (8/2 +0,3 ∙ 8) +
+ 68,14 ∙ 1,3 ∙ 8 – 75,03 – 8,24 ∙ 0,4 ∙ 24 + 115,62 ∙ 0,3 ∙ 8 =
= 6244,884 – 6244,870 = 0,014 кН ∙ м.
Точность подсчетов приемлемая. Рама находится в равновесии, значит, расчет выполнен верно.
k
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
.
кН;
кН.
Рисунок 19