Вейвлетные пакеты. Волновые пакеты. Основные параметры - частота, масштаб и положение, страница 5

Базисные функции  хорошо локализованы по времени и по частоте. По времени локализация определяется длиной интервала . Спектр   состоит из 2-х всплесков на частотах  и , с шириной, равной ширине спектра . Выбирая  гладкую функцию , можно получить достаточно малую ширину спектра и хорошую локализацию.

Суперпозиция функций  может быть изображена как последовательность огибающих базисных функции (рис. 10). Вертикальные линии проведены в точках условных границ базисных функций.

Возможно вычисление нескольких локальных тригонометрических преобразований сразу, рекурсивно разделяя интервалы пополам. Базисная функция на каждом интервале есть прямая ортогональная сумма базисных функций на его левом и правом подинтервалах, то есть

, где ,и    - базисные функции для интервалов ,   и  соответственно.

Такое разбиение можно продолжать дальше рекурсивно, и все образующиеся базисы будут обладать свойством ортогональности. Полученное дерево напоминает дерево вейвлетных пакетов. Несколько уровней дерева локальных тригонометрических базисов изображено на рис. 11.

Дискретизированный косинус с полу-целыми частотами является базисной функцией стандартного быстрого дискретного косинусного преобразования (ДКП).  Поэтому для нахождения коэффициентов локального тригонометрического преобразования, вместо вычисления скалярного произведения (21), может быть использован алгоритм ДКП после предварительной операции «складывания» (folding). Эту операцию можно наглядно представить как «складывание» перекрывающихся частей функций  внутрь интервалов. Пусть необходимо «сложить» функцию в точке , на интервалах  и , которым соответствуют функции  и . «Складывание» заменяет функцию  её левой  и правой частями

;

.                             (22)

Симметрия  (19) позволяет использовать  вместо функции , связанной с левым подинтервалом  .

Восстановление  по известным  и   возможно по следующим формулам

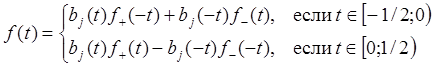.                    (23)

Эту операцию можно применять аналогично для любых соседних интервалов.

«Складывание» разбивает сигнал  на набор таких локальных сигналов , что применение ДКП к отсчетам   эквивалентно вычислению скалярного произведения сигнала с функциями , то есть

,                                                          (24)

где    

                                                          (25)

и 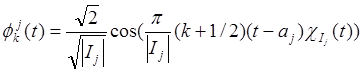       .         (26)

Функция  равна 1, если , и равна 0 в противоположном случае.

Если сигнал  дискретизирован в точках  , то можно сначала «сложить» его на границах всего интервала и получить , далее рекурсивно «складывать» в средних точках интервалов на нескольких уровнях до выбранной минимальной длины интервала. Эта процедура разделяет каждую функцию  на две  и , как показано на рис. 12.

После этого можно вычислить ДКП для каждого , и получить спектральное дерево (рис. 13).

Используя определение энтропии для отсчетов (17.1), можно ввести понятие адаптивного спектра для локального тригонометрического преобразования в смысле минимизации энтропии. Адаптивный локальный спектр  для временного интервала  определяется рекурсивно через спектры на подинтервалах  следующими формулами, аналогичным формулам получения «наилучшего» базиса для вейвлетных пакетов

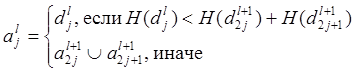.                     (27)

Если начать эту процедуру с   на некоторой глубине  разложения, тогда  будет содержать коэффициенты локального тригонометрического преобразования, с таким разбиением на подинтервалы, которое минимизирует энтропию. Выбранное разделение на подинтервалы называется адаптивным (минимизирующим энтропию) временным разбиением для данного сигнала.

Применение локальных тригонометрических базисов к обработке речевых сигналов

Пусть  - речевой сигнал, дискретизированный на временном интервале , и вычислено его адаптивное временное разбиение .