 |
Для приведения исходного уравнения f(x) = 0 к виду x = y(x) может быть применен достаточно общий прием, обеспечивающий выполнение неравенства y/(x) < 1: функция определяется следующим образом:
y(x) = x - 1/M*f(x), где коэффициент M представляет собой наибольшее значение модуля производной f/(x) на отрезке [a; b] , взятое с тем же знаком, что и производная f/(x) на этом отрезке.
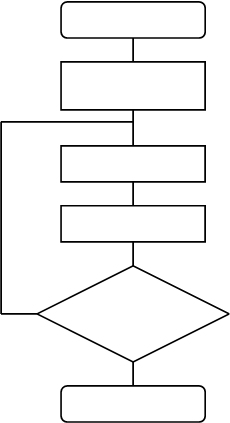
Схема алгоритма уточнения корня методом итераций приведена на рис. 2. Входными параметрами алгоритма являются a, b - границы интервала изоляции корня; E - погрешность вычисления, q - максимальное значение модуля производной y/(x) на интервале [a; b] .
Начальное значение корня x можно принять равным a + b / 2 (блок 2). Переменная y используется для запоминания предыдущего приближения корня (блок 3), в блоке 4 вычисляется очередное приближение корня по основной итерационной формуле. Выходным параметром алгоритма является корень уравнения x.
3. Метод Ньютона
Для обеспечения сходимости метода Ньютона (метода касательных) необходимо, чтобы производные f/(x) и f//(x) были определены, непрерывны и сохраняли постоянные знаки на отрезке [a; b].
Выберем некоторую точку x0 отрезка [a; b] и проведем в точке P0 {x0, f(x0)} касательную к кривой y = f(x). Ее уравнение:
y = f(x0) + f/(x0)(x - x0 ).
Новое приближение корня x1 равно абсциссе точки пересечения касательной с осью Ox: x1 = x0 - f(x0) / f/(x0). Проведя касательную через точку P1 {x1; f(x1)}, получим второе приближение корня x2. Процесс вычисления приближений по формуле
xn+1 = xn - f(xn) / f/(xn) (1)
продолжаем до выполнения неравенства xn+1 - xn <= E.
Начальное приближение x0 необходимо выбрать так, чтобы
f(x0) * f//(x0) > 0 (2)
В противном случае сходимость метода Ньютона не гарантируется. Обычно выбирают x0 = b, в зависимости от того, для какой из этих точек выполняется условие (2).
Рис. 3 Входные параметры (а,b,e)
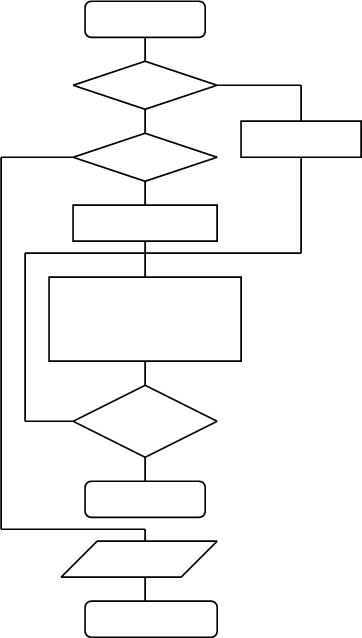 |
Схема алгоритма уточнения корня уравнения методом Ньютона приведена на рис. 3. Входными параметрами являются значения переменных a, b, E. Блоки 2 - 5 служат для выбора начального приближения корня. Если условие f(x0) * f//(x0) > 0 не выполняется для границ отрезка [a; b] (ветвь “Нет” блока 4), то выводится сообщение об ошибке и вычисления прекращаются (необходимо проверить условия сходимости метода Ньютона). Переменная h - приращение переменной x (h = xn+1 - xn). Выходным параметром алгоритма является корень уравнения x.
Если производная f/(x) мало изменяется на отрезке [a; b], в чем можно убедиться при предварительном исследовании функции f(x), то ее вычисление можно вынести из итерационного цикла, что сократит время вычислений.
4. Метод половинного деления
Если вид функции f(x) достаточно сложный, то вычисление функций f/(x) в методе Ньютона и y/(x), необходимой для оценки сходимости в методе итераций, затруднительно. Для решения таких уравнений можно использовать метод половинного деления, который всегда приводит к искомому результату, хотя и требует большего объема вычислений.
Для нахождения корня уравнения f(x) = 0, принадлежащего отрезку [a; b], делим отрезок пополам, т.е. выбираем начальное приближение равным x0 = (a +b) / 2. Если f(x0) = 0, то x0 - корень уравнения. В противном случае выбираем тот из отрезков [a; x0] или [x0; b], на концах которого функция f(x) имеет противоположные знаки (т.е. отрезок, содержащий корень уравнения). Новый отрезок [a; b] вновь делим пополам и повторяем процедуру до тех пор, пока длина отрезка, содержащего корень, не станет меньше заданной погрешности E.
Схема алгоритма уточнения корня уравнения методом половинного деления приведена на рис. 4.
Рис.4 Входные параметры (a,b,e)
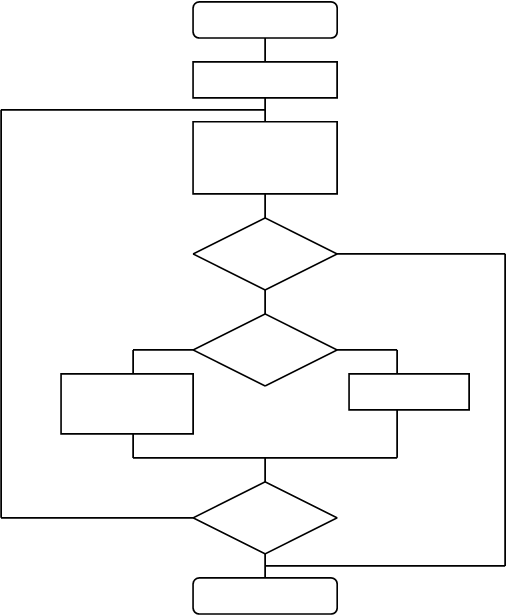 |
В схеме алгоритма:
2 - вычисление значения функции f(a);
3 - расчет координаты x середины интервала [a; b] и
вычисление значения функции f(x);
4 - проверка условия f(x) = 0.
Если условие выполняется, то x - корень уравнения, - выход из алгоритма;
5-7 - определение нового отрезка [a; b], содержащего корень;
8 - присвоение значения y = f(x) переменной z, если граница a сдвигается в точку x;
9 - проверка условия окончания вычисления корня.
5. Метод хорд
Проведем через точки (a, f(a)) и (b, f(b)) прямую.
Ее уравнение:
(y - f(a)) / (f(b) - f(a)) = (x - a) / (b - a).
Начальное приближение корня равно абсциссе точки пересечения прямой и оси Ox:
x0 = a - [(b - a) / (f(b) - f(a))] * f(a) (3)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.