В математике множеством называют совокупность, набор каких-либо предметов, объектов. Это не является точным математическим определением. Так же как понятие числа, понятие множества является одним из первичных, наиболее общих понятий, которые принимаются без определения.
Объекты, составляющие множество, называются его элементами.
То, что элемент а принадлежит множеству А , записывается так: ![]() ; а если не принадлежит, то так:
; а если не принадлежит, то так: ![]() . Имеет смысл рассматривать множество, не
содержащее ни одного элемента. Оно называется пустым и обозначается
символом
. Имеет смысл рассматривать множество, не
содержащее ни одного элемента. Оно называется пустым и обозначается
символом ![]() .
.
Задать множество можно, либо предъявив перечень его элементов (только для конечных множеств), либо указав правило для определения того, принадлежит или нет данный объект рассматриваемому множеству.
Если А и В – множества, то запись ![]() означает, что они состоят из одинаковых
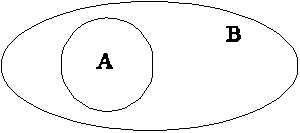
элементов. Если все элементы множества А являются элементами множества В,
то говорят, что А – подмножество В и пишут
означает, что они состоят из одинаковых
элементов. Если все элементы множества А являются элементами множества В,
то говорят, что А – подмножество В и пишут ![]() . Пустое
множество является подмножеством любого множества.
. Пустое
множество является подмножеством любого множества.
 |
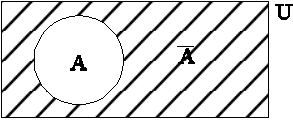
Пусть мы рассматриваем только множества, которые
являются всевозможными подмножествами данного множества U. В
этом случае исходное множество U называется универсальным множеством. Рассмотрим,
например, множество U , состоящее из двух элементов: ![]() . Перечислим все подмножества U :
. Перечислим все подмножества U :![]() ,
, ![]() ,
, ![]() ,
, ![]() . Всего
их
. Всего
их ![]() . Можно доказать, что если универсальное
множество состоит из n элементов, то число всех его подмножеств равно
. Можно доказать, что если универсальное
множество состоит из n элементов, то число всех его подмножеств равно ![]() .
.
 |
1.
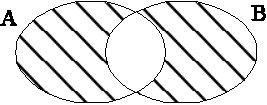
Объединением ![]() двух множеств А и В называется
множество, состоящее из всех элементов, принадлежащих по крайней мере одному из
множеств А и В. Соответствующая диаграмма Венна имеет вид:
двух множеств А и В называется
множество, состоящее из всех элементов, принадлежащих по крайней мере одному из
множеств А и В. Соответствующая диаграмма Венна имеет вид:
 |
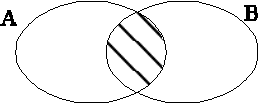 |
3. Разностью ![]() множеств
А и В называется множество, состоящее из всех элементов А, не входящих в В:
множеств
А и В называется множество, состоящее из всех элементов А, не входящих в В:

 |
Пример.
Симметрическая разность выражается через другие операции: ![]() . Обоснуем это с помощью диаграмм Венна.
Для этого построим диаграммы левой и правой частей равенства. Левая часть –
симметрическая разность – изображена выше. Чтобы построить правую, нарисуем
множества А и В, а затем будем заштриховывать различным образом множества,
получающиеся при операциях в формуле (в порядке выполнения последних).
Заштрихуем вертикально
. Обоснуем это с помощью диаграмм Венна.
Для этого построим диаграммы левой и правой частей равенства. Левая часть –
симметрическая разность – изображена выше. Чтобы построить правую, нарисуем
множества А и В, а затем будем заштриховывать различным образом множества,
получающиеся при операциях в формуле (в порядке выполнения последних).
Заштрихуем вертикально ![]() , потом горизонтально
, потом горизонтально ![]() :
:

Тогда разность этих множеств будет состоять, по определению, из всех элементов, заштрихованных либо вертикально, либо горизонтально, но не горизонтально и вертикально одновременно. Сравнение с диаграммой для левой части завершает рассуждение.
Некоторые свойства объединения и пересечения множеств очень похожи на свойства операций сложения и умножения чисел. В то же время многие свойства введенных операций со множествами отличаются от свойств алгебраических операций. Перечислим основные из них.
1. ![]() и
и ![]() - коммутативность объединения и
пересечения множеств.
- коммутативность объединения и
пересечения множеств.
2. ![]() и
и ![]() - ассоциативность объединения и
пересечения множеств.
- ассоциативность объединения и
пересечения множеств.
3. ![]() - дистрибутивность
пересечения относительно объединения;
- дистрибутивность
пересечения относительно объединения; ![]() -
дистрибутивность объединения относительно пересечения.
-
дистрибутивность объединения относительно пересечения.
4.
![]()
![]() - законы де Моргана.
- законы де Моргана.
5.
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
6.
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Все эти свойства могут быть выведены непосредственно из определений или с помощью диаграмм Венна.
Пример.
Докажем равенство ![]() . Изобразим левую сторону.
Заштрихуем А горизонтально,
. Изобразим левую сторону.
Заштрихуем А горизонтально, ![]() - вертикально. На
диаграмме пересечению этих множеств соответствует область, заштрихованная двумя
способами одновременно. Изобразим правую сторону. Заштрихуем
- вертикально. На
диаграмме пересечению этих множеств соответствует область, заштрихованная двумя
способами одновременно. Изобразим правую сторону. Заштрихуем ![]() горизонтально, а
горизонтально, а ![]() -
вертикально. На диаграмме объединению этих множеств соответствует
заштрихованная область.
-
вертикально. На диаграмме объединению этих множеств соответствует
заштрихованная область.

Сравнивая две диаграммы, получаем требуемое равенство.
Определение. Функцией алгебры логики f от n переменных называется отображение:
![]() .
.
Назовем элементарными следующие функции алгебры логики одной и двух переменных:
Таблица 1
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.