В основе предмета о физическом подобии лежит идея о независимости закона природы от конкретной системы мер, выбранной исследователем.
Основная теорема подобия: физически подобные процессы – те, у которых безразмерные поля, характеризующие их одноименные величины, тождественны (поля скорости температур) в геометрически подобных конфигурациях при турбулентном и ламинарном течении (или два физические явления подобны, если они имеют одинаковое математическое описание (физическое подобие), равенство соответствующих критериев подобия и идентичность условий однозначности). Механически подобными течениями называются течения с геометрически подобными картинами линии тока.
Для выполнения механического подобия необходимо, чтобы во всех подобно расположенных точках силы, действующие на элемент объема жидкости, находились в одинаковом отношении одна к другой во все моменты времени.
Имеются только силы трения и силы инерции:
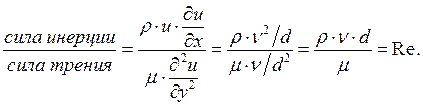
Каждая точка критериальной функции соответствует группе подобных явлений. Критерии подобных явлений справедливы как для сжимаемых, так и несжимаемых течений.
Теория подобия позволяет, не решая основной системы уравнений, выделить безразмерные (определенные) компоненты (критерии), которые определяют решение.
При этом значительно уменьшается число определяемых факторов, и решение получается в наиболее общем виде.
Введём для нестационарного режима течение понятие критерия подобия Био:
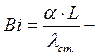 отношение внутреннего термического сопротивления теплопроводности к
внешнему термическому сопротивлению теплоотдачи
отношение внутреннего термического сопротивления теплопроводности к
внешнему термическому сопротивлению теплоотдачи ![]()
1) для шара: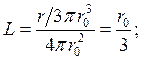 2) для цилиндра:
2) для цилиндра: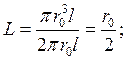 3) для куба:
3) для куба: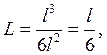
где ![]() сторона
куба.
сторона
куба.
В общем виде
решение имеет вид: ![]()
Таким образом,
критерий подобия Био характеризует неравномерность температурного поля в теле. При
![]() тепло проходит «транзитом»
сквозь стенку и температура не изменяется (нет температурного перепада), а при
тепло проходит «транзитом»
сквозь стенку и температура не изменяется (нет температурного перепада), а при![]() тепло скапливается вблизи
поверхности. Такие случаи бывают на ракетах – «тонкая стенка» (в
тепловом отношении нет перепада температур
тепло скапливается вблизи
поверхности. Такие случаи бывают на ракетах – «тонкая стенка» (в
тепловом отношении нет перепада температур ![]() ).
).
Введём критерий подобия Фурье:
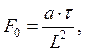
где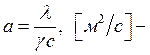 коэффициент
температуропроводности, характеризующий темп прогрева или охлаждения тела. Величина
обратная
коэффициент
температуропроводности, характеризующий темп прогрева или охлаждения тела. Величина
обратная ![]()
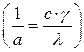 называется
тепловой инерцией тела.
называется
тепловой инерцией тела.
Критерий подобия
Фурье – мера тепловой насыщенности тела; характеризует нестационарность
процесса. Чем больше![]() тем ближе стенка к полному
прогреванию.
тем ближе стенка к полному
прогреванию.
Критерии подобия Био и Фурье относятся к теплообмену теплопроводностью в твёрдых телах (нестационарная задача) и соответственно, учитывают физические свойства тел и временные характеристики.
Критерий подобия Прандтля, характеризующий теплофизические свойства среды:
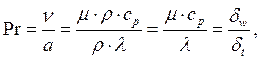
где ![]() толщина
гидродинамического слоя;
толщина
гидродинамического слоя; ![]() толщина
температурного слоя.
толщина
температурного слоя.
Критерий Эйлера, который следует из уравнения движения и характеризует соотношение перепада статических давлений к динамическому напору:
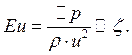
В реальном напоре всегда есть потери полного давления.
Критерий Архимеда, учитывающий массовые силы – отношение подъемной силы к силе вязкого трения:
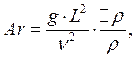
где ![]() ускорение
свободного падения;
ускорение
свободного падения; ![]() характерный размер;
характерный размер; ![]() кинематическая вязкость;
кинематическая вязкость;
![]() характерная
плотность, где
характерная
плотность, где ![]() коэффициент теплового
расширения;
коэффициент теплового
расширения;
![]() разность
температур, обусловливающих движение.
разность
температур, обусловливающих движение.
Критерий Грасгоффа – частный вид критерия Архимеда для тепловой гравитационной (свободной) конвекции:
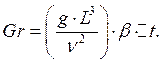
Критерий Галилея:
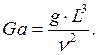
Критерий турбулентности:
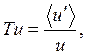
где ![]() пульсационная
скорость.
пульсационная
скорость.
Критерий С. С. Кутателадзе, который вводят при фазовых переходах:
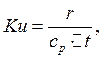
где ![]() теплота
фазового перехода.
теплота
фазового перехода.
В реальной практике используют комбинированные критерии подобия.
Критерий Пеклé для несжимаемой жидкости:
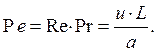
Критерий Рэлея:
![]()
Искомыми переменными в безразмерном виде являются критерии Нуссельта и Стантона.
Критерий Нуссельта, который можно получить из дифференциального уравнения теплоотдачи методом масштабных преобразований – показывает во сколько раз теплоотдача больше теплопроводности:
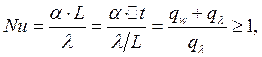
где ![]() теплота
за счет конвекции;
теплота
за счет конвекции; ![]() теплота за счет
теплопроводности.
теплота за счет
теплопроводности.
Если ![]() то конвекции нет, только
тепловодность.
то конвекции нет, только
тепловодность.
Получим искомое
решение в безразмерном виде: ![]() где
где ![]() локальное число Нуссельта;
локальное число Нуссельта; ![]() безразмерная координата.
безразмерная координата.
Введём
понятия критерия Стантона ![]() и локального
коэффициента сопротивления трению
и локального
коэффициента сопротивления трению ![]()
Критерий Стантона – безразмерный коэффициент теплоотдачи:
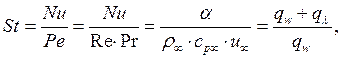
где
коэффициент теплоотдачи ![]()
Тогда
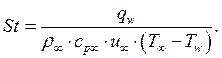
Локальный коэффициент сопротивления трению:
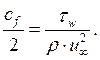
Используя выше приведенные выражения, получим:
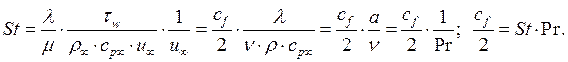
Если ![]() то
то ![]() справедливо
только для пластины.
справедливо
только для пластины.
Важный
вывод: механизм переноса импульса и тепла один и тот же. Если известен St,
то можно определить ![]() и наоборот.
и наоборот.
Критерий подобия Эккерта, который связан с выделением тепла при адиабатическом сжатии:
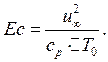
где![]() разность температур тела и потока.
разность температур тела и потока.
Проведя некоторые преобразования, получим:
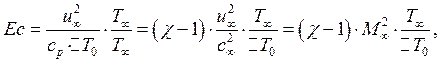
где
число Маха: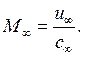
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.