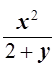 +
+ 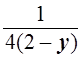 = 1.
= 1.
Поскольку x2 = 4 – y2, приведем последнее уравнение к виду
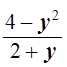 +
+ 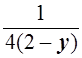 = 1.
= 1.
Видя, что каждое слагаемое левой части неотрицательное, оценим левую часть:
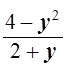 +
+ 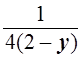
![]() 2
2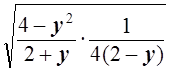 =
=
= 2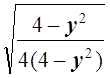 = 2
= 2![]() =
= ![]() = 1.
= 1.
Теперь ясно, что исходное уравнение равносильно системе
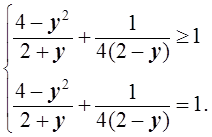
Неравенство этой системы обращается в равенство тогда, когда
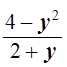 =
= 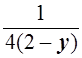 , т.е. 2 – у =
, т.е. 2 – у = 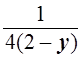 .
.
Дальше все проходит автоматически:
![]() = 1
= 1![]()
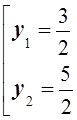
![]()
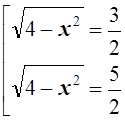
![]()
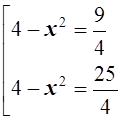
![]()
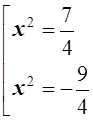
![]()
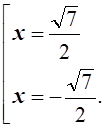
Оба полученных корня принадлежат промежутку [-2;0) ![]() (0;
2].
(0;
2].
О т в е т: x1,2= ± ![]() .
.
3. Решить уравнение: ![]() +
+ ![]() = 2xy–1 .
= 2xy–1 .
Р е ш е н и е. Перепишем в виде:
![]() +
+ ![]() = 4xy–2 .
= 4xy–2 .
неравенство Коши.
![]() +
+ ![]()
![]() 2
2![]() = 2x2y2
= 2x2y2
Имеем
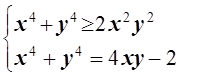
![]() 4xy – 2
4xy – 2 ![]() 2x2y2
2x2y2
Из исходного неравенства, получим:
x2 y2 – 2xy + 1 ![]() 0,
0,
(xy – 1)2 ![]() 0,
0, ![]() xy
= 1,
xy
= 1, ![]() y =
y = ![]() .
.
x4 + ![]() = 2, x
= 2, x ![]() 0;
0;
x8 – 2x4 + 1 = 0;
(x4 – 1)2
= 0; x4 = 1; x = ![]() 1; y =
1; y = ![]() 1;
1;
Ответ: x = ![]() 1; y =
1; y = ![]() 1.
1.
Опишем теперь способ, с помощью которого будут решены остальные уравнения этого пункта. Как и в предыдущих случаях, основой способа является неравенство Коши. Но оно теперь будет применяться к уравнениям вида
![]() = g(x).
= g(x).
Сначала оценивают каждый арифметический корень левой части уравнения с учетом показателя степени корня, для чего подкоренное выражение представляют в виде произведения множителей, количество которых определяется показателем степени корня. Например,
![]() =
= ![]()
![]()
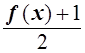 ,
, ![]() =
= ![]()
![]()
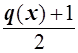 .
.
Затем складывают полученные оценки и записывают неравенство
![]()
![]()
![]() (x), где φ(x) =
(x), где φ(x) = 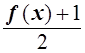 +
+ 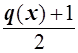 .
.
Таким образом, получают систему
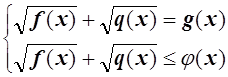 , а из нее – неравенство
, а из нее – неравенство ![]() (x)
(x) ![]() g(x).
g(x).
Теперь остается определить, при каких x достигается равенство
в неравенстве ![]() (x)
(x) ![]() g(x).
g(x).
Приведем ряд задач, в которых применяется этот способ.
4. Решить уравнение: ![]() .
.
Р е ш е н и е. Оценим каждый арифметический корень левой части уравнения. Учитывая, что подкоренные выражения неотрицательны, имеем:
![]()
![]()
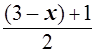 =
=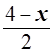 ;
; ![]() =
=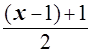 =
=![]()
Найдем сумму полученных выражений:
![]()
![]()
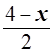 +
+ ![]() = 2, т.е.
= 2, т.е. ![]()
![]() 2.
2.
Преобразуем теперь правую часть исходного уравнения:
![]() =
(
=
(![]() ) + 2 = (
) + 2 = (![]() )2
+ 2
)2
+ 2
![]() 2, сравнивая
2, сравнивая
![]() и
и ![]()
получим
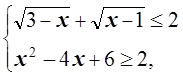
откуда
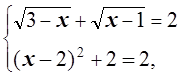
и, следовательно, x= 2.
Остается проверить, удовлетворяет ли найденное значение x области допустимых значений неизвестного. Из условий
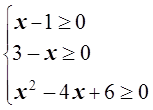
следует, что 1![]() x
x![]() 3,
т.е. 2
3,
т.е. 2![]() [1; 3].
[1; 3].
О т в е т:x= 2.
5. Найдите все пары чисел (x; у), удовлетворяющие уравнению:
![]() +
+ ![]() = 2 –
= 2 – 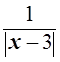 .
.
Р е ш е н и е. Запишем исходное уравнение в виде:
![]() +
+ 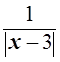 = 2 –
= 2 – ![]() .
.
Используя неравенство Коши и неотрицательность модуля действительного числа, найдем оценки для левой и правой части уравнения:
![]() +
+ 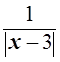
![]() 2
2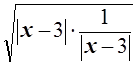 = 2, 2 –
= 2, 2 – 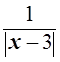
![]() 2.
2.
Видим, что в первом случае равенство достигается
только тогда, когда ![]() =
=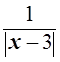 ,
,
а во втором ![]() . Из этих данных и находим решение: (x – 3)2 =1, т.е. x
равно 2
. Из этих данных и находим решение: (x – 3)2 =1, т.е. x
равно 2
или 4. Отсюда находим, ![]() = 4 или
= 4 или ![]() = 2, т.е. y равен 2 или 16.
= 2, т.е. y равен 2 или 16.
О т в е т: (4; 16)![]() (2;2).
(2;2).
6. Решить систему уравнений:
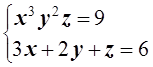 ,
если x > 0,y> 0, z> 0.
,
если x > 0,y> 0, z> 0.
Р е ш е н и е. В
силу того, что x > 0,y> 0, z> 0, первое уравнение
системы Можно записать в виде ![]() . Оценив левую часть этого уравнения с учетом показателя степени корня,
получим
. Оценив левую часть этого уравнения с учетом показателя степени корня,
получим
![]() =
= ![]()
![]()
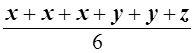 =
= 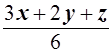 = 1.
= 1.
Подставили второе уравнение в
неравенство и получили ![]()
![]() 1.
1.
Так как ![]() , делаем вывод, что
, делаем вывод, что ![]()
![]() 1. Но
последнее неравенство неверно, значит, данная система не имеет решений.
1. Но
последнее неравенство неверно, значит, данная система не имеет решений.
О т в е т: решений нет.
1)Углубленное изучение курса алгебры и математического анализа.М. Л. Галицкий, Москва “Просвещение”, 1990г.
2) Алгебра и математического анализ. 11 кл. Н.Я. Виленкин и др.
Москва “Просвещение”, 1995 г.
журнал. 2002 г.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.