Математический анализ. Дифференциальное и интегральное исчисления

целый»; интегрирование — процесс объединения в целое малых элементов, из которых составлены фигура, тело и т. п. (Вначале Лейбниц предлагал термин «сумматорное исчисление».)

У Лейбница сразу же появились последователи, наиболее прославились братья Иоганн и Якоб Бернулли. Термин «анализ» впервые встречается в заглавии учебника «Анализ бесконечно малых величин» (1696 г.), написанного учеником Иоганна Бернулли — Гийомом де Лопиталем.

Подход Лейбница был геометрическим: он стремился дать общий метод определения касательной к кривым и научиться вычислять площади фигур, ограниченных графиками функций. Предшественниками Лейбница являлись великие геометры древности. Архимед вплотную подошёл к интегральному исчислению, определяя площади и объёмы фигур — круга, шара, цилиндра, сегмента параболы. Его идеи развил в XVII в. итальянец Бонавентура Кавальери, который создал метод «неделимых» (по сути дела, бесконечно малых). Касательные к различным кривым изучали в XVII столетии Рене Декарт, Блез Паскаль, Пьер Ферма и Христиан Гюйгенс. Последний оказал на Лейбница особенно сильное влияние.

 

Ньютон пришёл к анализу, исходя из необходимости описывать движение тел и эволюцию различных процессов. Он мыслил как физик, кинематически: если функция x(f) задаёт путь, пройденный телом к моменту времени t, то естественно возникает понятие скорости v(f) в данный момент. Она примерно равна отношению пути, пройденного телом за очень малый отрезок времени t (т. е. , к t, а точно — пределу этого отношения, когда t стремится к нулю. Скорость тела в момент t Ньютон обозначил x(f) и назвал флюксией (от лат. fluctio — «течь», «струиться»). В современной математике приняты термин «производная» и обозначение x'(t), физики же чаще пользуются символом x(f).

Сочинение Ньютона «Метод флюксий и бесконечных рядов», написанное в 1670—1671 гг., было опубликовано посмертно, в 1736 г. Суть дифференцирования, по Ньютону, — нахождение скорости по пути, т. е. x(f) no x(f); интегрирование — обратная операция, а именно восстановление пути по скорости. Иначе говоря, интегрирование — это решение простейшего дифференциального уравнения         

Во всём этом Ньютон принял эстафету от родоначальников современного естествознания — Галилео Галилея и Иоганна Кеплера.

Созданный Ньютоном математический аппарат привёл его к фундаментальной концепции, которую учёный выразил сначала в зашифрованном виде анаграммой. Её суть можно передать словами: «Мир управляется диффеИоганн Кеплер

ренциальными уравнениями». В «Математических началах натуральной философии» (1687 г.) Ньютон описал механическую систему мира, в частности, опираясь на закон всемирного тяготения, сформулировал законы движения небесных тел во Вселенной.

Всеобщее признание и последовавшее за ним бурное развитие классической механики Ньютона укрепили позиции детерминизма — философского принципа, согласно которому все явления природы полностью предсказуемы, если имеется исчерпывающая информация о состоянии мира в какой-то момент времени (начальные данные). Простейшим примером такой предопределённости является возможность описать путь x(f) некоего тела, если известна его скорость v(f) на отрезке [О, Т]. Для этого достаточно задать начальное данное — координату х(0) положения тела в начальный момент времени.

Грандиозные успехи естествознания и математики в последующие три столетия во многом были определены великим открытием Ньютона и Лейбница. В XVIII в. свой вклад в развитие математического анализа внесли братья Иоганн и Якоб Бернулли, Леонард Эйлер, Жозеф Луи Лагранж, Пьер Симон Лаплас и другие учёные. Образно говоря, они старались захватить возможно большие территории, не заботясь о том, чтобы как можно лучше освоить уже имеющиеся. Представления о бесконечно малых и их суммировании они скорее воспринимали интуитивно, чем подвергали логическому анализу.

Только в XIX в. были даны строгие определения функции, непрерывности, производной. Современное понятие функции сформировалось в первой половине XIX в. благодаря исследованиям таких выдающихся математиков, как Николай Иванович Лобачевский, Петер Густав Лежён Дирихле и др. Производная была определена как предел отношения приращения функции к приращению аргумента (Опостен Коши); интеграл — как предельное значение интегральных сумм, т. е., по сути дела, площадей под графиком кусочно-постоянных («ступенчатых») функций, приближающих данную (интегрируемую) функцию (Бернхард Риман). До сих пор математическое образование основывается на этих подходах, хотя в XX в. они получили значительное развитие. Тогда же вошли в употребление термины «элементарная» и «высшая» математика. (Под элементарной математикой обычно понимают ту математику, которая предшествовала рождению математического анализа; высшая начинается с понятий предела, производной и интеграла.)

Одним из важнейших завоеваний математического анализа в XIX в. стало рождение теории аналитических функций и функций комплексного переменного.

Теория аналитических функций во многом базируется на теории рядов, которая зародилась одновременно с математическим анализом. Первые разложения элементарных функций в ряды были получены в XVII в. Эйлер научился разлагать в ряды большинство элементарных функций. Теорию аналитических функций построил Коши.

Геометрия, явившаяся одним из краеугольных камней, на которых зиждется математический анализ, в XVIII—XIX вв. развивалась в значительной мере независимо от него. В XX в., уже на новом уровне, происходит всё большее слияние геометрии и анализа. Областью приложения анализа становятся многообразия — кривые и поверхности, расположенные в многомерных пространствах, обладающих, как правило, дополнительной алгебраической структурой (группой движений и т. п.).

ИНТЕГРАЛ  И ПЕРВООБРАЗНАЯ ФУНКЦИИ

Внедрение элементов математического анализа в курс математики средней школы поставило перед математиками, методистами и учителями сложные и разнообразные задачи. Тема « Первообразная и интеграл» - одна из главных в курсе « Алгебра и начала анализа» и по содержанию материала, и по тем приемам  учебной деятельности, которые могут и должны быть сформированы  при изучении данной темы и применены к решению разнообразных задач теоретического и прикладного характера.

Представим себе, что по дороге движется автомобиль. Стрелка спидометра замерла на отметке 100 км/ч, а счётчик пройденного расстояния... заклеен непрозрачной бумагой. Можно ли сказать хотя бы что-нибудь о показаниях счётчика? Конечно. Ясно, например, что в любой момент он показывает ровно на 100 км большее расстояние, чем час назад. Построим

Рис. 1.

 

график зависимости скорости от времени v(t) = v₀ = const (рис. 1). Если S(t) — путь, пройденный автомобилем начиная с какого-то момента времени t0, то расстояние, которое он покроет за промежуток времени от t_H до t_k, равно S(t_h- t_k) = v₀(t_K - t_H). Обратите внимание, что эта величина равна площади прямоугольника, ограниченного снизу осью абсцисс, сверху — графиком функции v(f) = v0, а слева и справа — вертикальными прямыми t = t_H,  t = t_K (рис. 2).

А что делать, если скорость непостоянна? Выделим в интервале времени от t_H до t_K какой-нибудь промежуток t, настолько малый, что скорость автомобиля не успеет сколько-нибудь заметно измениться в течение этого t. Средняя скорость на промежутке  незначительно отличается от мгновенной скорости в любой момент времени t из данного промежутка. А потому расстояние, пройденное автомобилем за время t, примерно равно v(t)  t.

Теперь, если разбить отрезок времени от t_H до t_K на много маленьких промежутков продолжительностью , а затем сложить найденные

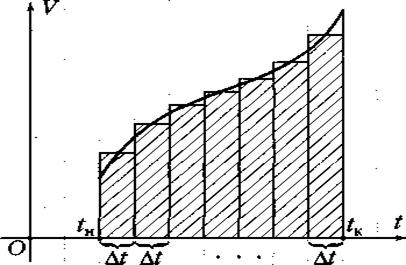
Рис. 3.

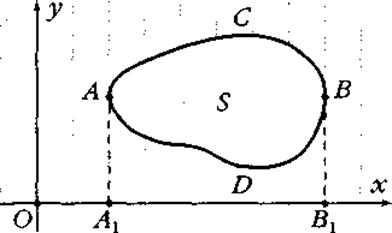
Рис. 4.

для них расстояния S = v(t) t, то можно с хорошей точностью вычислить S(t_K) - S(t_H). При этом чем уже промежуток t (т. е. чем на большее число промежутков разбит отрезок [t_H, t_k], тем ближе к действительному значению S(t_K) - S(t_H). будет найденная сумма.

На рис. 3 ей соответствует площадь заштрихованной ступенчатой фигуры. При стремлении t к нулю фигура стремится к криволинейной трапеции под графиком функции (показана жёлтым цветом), а её площадь — к площади трапеции. Эта величина называется определённым интегралом функции v(t) на отрезке [t_H t_K] и обозначается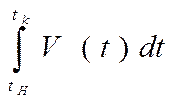              

К вычислению определённого интеграла сводится множество задач. Рассмотрим некоторые из них.

1. Пусть на координатной плоскости задана выпуклая криволинейная фигура, ограниченная графиками функций f(x) и g(x). Требуется узнать её площадь.

Проведём две вертикальные касательные АА₁ и ВВ₁ (рис. 4). Очевидно, что искомая площадь равна разности площадей двух криволинейных трапеций: А₁АСВВ₁ и A₁ADBB₁. Поэтому если абсцисса точки А равна x₁ точки В — х₂, то

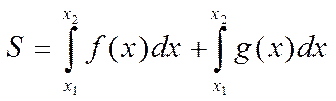
2.  Возьмём тонкий неоднородный стержень, один из концов которого примем за начало. Пусть линейная плотность материала стержня на расстоянии х от начала равна p(x). Нужно найти массу стержня.

Мысленно разобьём стержень на короткие кусочки Ах Определим массу каждого кусочка (она приблизительно равна P(x) x) и сложим эти массы. Не правда ли, мы действуем так же, как и в задаче, в которой определяли расстояние по скорости? А потому и искомая величина равна площади криволинейной трапеции под графиком функции, т. е. интегралу

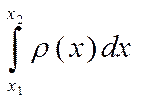
3. Работа, как известно, равна произведению силы на перемещение. Если же сила меняется с расстоянием, то приходится разбивать весь путь на маленькие отрезки s, в пределах которых сила F практически не меняется. Тогда работа на каждом таком отрезке равна Fs, a общая работа — сумме всех «микроработ»                    

ПЕРВООБРАЗНАЯ

Задача с движущимся автомобилем подсказывает способ нахождения определённых интегралов. В самом деле, если S(f) — путь, пройденный автомобилем за время t, то его скорость v(t) — это производная пути:

V(t)= S’(t)

Таким образом, если нам известна функция v(t), то нужно подобрать такую функцию S(t), производная которой была бы равна v(t). Например, если v(t) = at (при равноускоренном движении), то в качестве S(t) можно взять любую функцию вида S(t) = at /2 + С, где С — некоторая константа, так как

Зная S(t), уже несложно вычислить интеграл

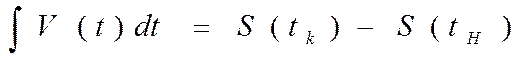
В частности, Функция F(x), производная которой равна данной функции/(л:), называется её первообразной. Так, функция F(t) = at²/2 есть первообразная для функции  F(t)= at. Поскольку производная константы равна нулю, первообразная определена с точностью до постоянного слагаемого, т. е. если F(х) есть первообразная функции f(x), то G(x) = F(x) + С тоже её первообразная. Для любой первообразной F(х) функции f(x) справедлива формула Ньютона — Лейбница

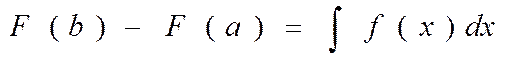
По сути дела, это всё та же формула (*), к которой нас привела задача о движущемся автомобиле. Формула Ньютона — Лейбница устанавливает связь между дифференциальным и интегральным исчислениями, а значит, между задачами о касательной и площади.

Семейство всех первообразных данной функции называется её неопределённым интегралом и обозначается

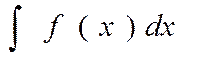
Если хотят записать формулу неопределённого интеграла какой-либо функции, то в конце формулы обязательно добавляют + С, подчёркивая тем самым, что это не какая-то одна первообразная, а множество всех первообразных данной функции. Например:

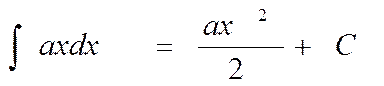
КАК НАЙТИ ИНТЕГРАЛ

Предположим, что мы хотим вычислить площадь криволинейной трапеции под графиком параболы y= х² на отрезке [0, а], где а — некоторое действительное число. Из рассмотренных выше примеров понятно, что искомая площадь равна интегралу

По формуле Ньютона — Лейбница, данный интеграл есть разность

F(a)-F(0)

где F(х) — первообразная функции f(x) = х². Как же найти эту первообразную?

Можно просто посмотреть в справочник (или в приводимую в нашей статье таблицу неопределённых интегралов). Но мы поступим иначе. Вспомним, что если F(х) — первообразная функции f(х), то F '(x) = f(x). Другими словами, интегрирование (т. е. в данном случае нахождение неопределённого интеграла) — задача, обратная дифференцированию. Поэтому мы обратимся к таблице производных (см. статью «Производная»), но воспользуемся ею не так, как положено, а наоборот — найдём такую функцию, производная которой «похожа» на функцию f(x) = х². Из всего, что там есть, как будто подходит формула

(x^a)’=ax^a-1

В её правой части стоит (а - 1)-я степень х. Нас интересует вторая степень, а потому будем считать, что а = 3:

(x³)’=3x²

Теперь, чтобы избавиться от коэффициента 3, вспомним: постоянный множитель можно выносить за знак производной, т. е.

(kx³)’= 3kx²

Положив k = 1/3, получим

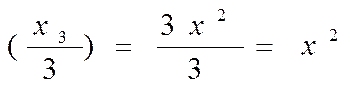
Итак, одной из первообразных функции f(x) = х² будет Р(х) = х³ /3, а все первообразные задаются формулой

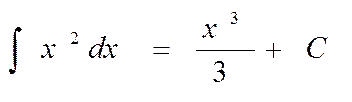
Попутно мы вывели одно из правил интегрирования:

Постоянный множитель можно выносить за знак интеграла:

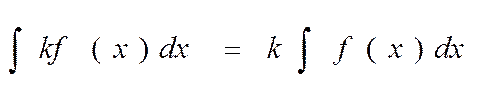
Интеграл суммы двух функций равен сумме интегралов этих функций:

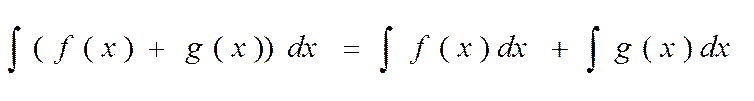
Однако вернёмся к нашей задаче. Нам осталось вычислить значения функции F(x) в точках х = 0  и  х = а, а затем вычесть первое из второго:

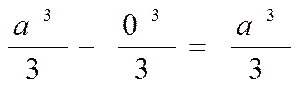
Таким образом, площадь криволинейной трапеции под графиком параболы  y= х2 на отрезке [0, а] равна a³/3.

Задачу о «квадратуре параболы» впервые решил древнегреческий учёный Архимед в III в. до н. э. (см. статью «Архимед»). В отличие от нас он рассмотрел общий случай параболы и доказал, что «произвольный сегмент, ограниченный прямой и параболой, равен 4/3 треугольника, имеющего те же основание и высоту» (рис. 6). Архимед также успешно находил площади и объёмы других фигур, несмотря на то что в математике его времени не было понятий интеграла и производной. Интегральное исчисление даёт общий метод решения всех подобных задач.

Первообразная и интеграл используются при  нахождении объема шара, объема наклонной призмы, объема пирамиды и объема конуса.

ОБЪЁМ ШАРА И ИНТЕГРАЛ

Одним из своих наивысших достижений Архимед считал доказательство того, что объём шара  в полтора раза меньше объёма описанного около него цилиндра:

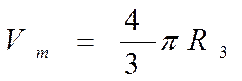
поскольку объём описанного цилиндра равен SH = nR² • 2R = 2л/R³. Недаром шар, вписанный в цилиндр, был высечен на надгробии Архимеда в Сиракузах. Это доказательство, как и вывод формулы объёма пирамиды с помощью «чёртовой лестницы», а также вычисление объёмов многих других тел, основаны на представлении тела в виде «стопки» тонких параллельных слоев. Объём каждого слоя примерно равен произведению площади его основания на толщину (слой — обобщённый цилиндр), так что, в сущности, нужно вычислить сумму площадей параллельных сечений, точнее, предельного значения произведения этой суммы на толщину слоя, когда последняя стремится к нулю. Математики прошлого проявляли немалую находчивость и остроумие в подобных вычислениях. Допустим, например, что для некоторого тела неизвестного объёма удалось подобрать

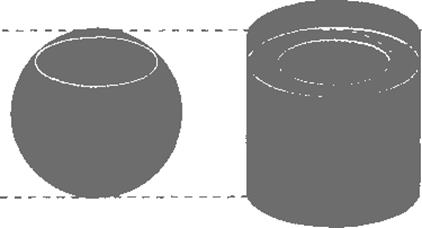
Рис. 9. Можно показать, что площадь любого сечения шара равна площади сечения той же плоскостью тела (изображено зелёным цветом), получаемого вырезанием из описанного около шара цилиндра двух конусов с обшей вершиной