Нестационарная стохастическая модель переменного роста для оценки стоимости некотируемых активов

Глава 21. Нестационарная стохастическая модель переменного роста для оценки стоимости некотируемых активов

Отсутствие цен на некотируемые активы не позволяет применить сравнительный подход. Остаются затратный (для финансовых активов – балансовый) и доходный подходы. В рамках доходного подхода наиболее подходящим является метод дисконтирования дивиденда (для оценки акций) и чистого денежного потока (для оценки бизнеса). Далее для определенности будем говорить об оценке бизнеса, и использовать соответствующую терминологию. Известными считаются только начальное значение чистого денежного потока и предполагаемые темпы его изменения в прогнозном периоде, который считается нестационарным. Необходимо определить инвестиционную стоимость актива. Для постпрогнозного периода, который предполагается стационарным эта задача изучалась в [5].

В главе также рассматриваются проблемы информационного обеспечения смешанной модели и, в частности, корректного экстраполирования ретроспективных статистических данных в прогнозном периоде, а также возможности использования экономических индексов для оценки неизвестной беты актива, которая в нестационарной модели будет зависеть от номера периода.

21.1. Стохастический аналог модели DDM переменного роста

Будем определять оценку текущей цены  актива в момент t, как условного математического ожидания приведенного потока доходов  по соответствующим ставкам дисконта , которые считаются внешними параметрами модели DDM переменного роста и предполагаются известными:

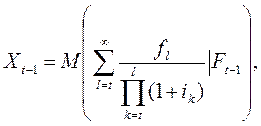                 (21.1)

где - алгебра, порожденная величинами  (ретроспективной информацией о потоке дохода до момента t), в предположении, что

где последовательность независимых случайных величин (с.в.) со средними значениями , которые считаются известными из прогноза.

Пусть

 , где номер последнего прогнозного года, то есть постпрогнозный период предполагается стационарным.

В силу независимости последовательности с.в. условное математическое ожидание величины  в формуле (1) будет равно:

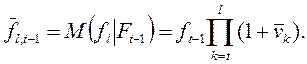        (21.2)

Вместе с (1) уравнение (2) дает стохастическую модель DDM переменного роста для текущей цены  актива, которая является случайной величиной как условное математическое ожидание и интерпретируется в модели как инвестиционная стоимость актива:

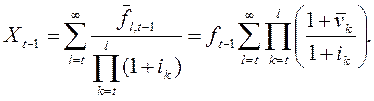              (21.3)                                                  

Предположим, что выполнено условие:

              (21.4)

Тогда ряд в формуле (21.3) сходится и справедлива формула Гордона для постпрогнозной стоимости актива [5]:

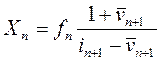
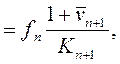                   (21.5)

где –– соответствующая ставка дисконта, определяемая по формуле

                   (21.6)

С учетом (21.5) уравнение (21.3) можно представить в виде обычного уравнения дисконтирования чистого денежного потока:

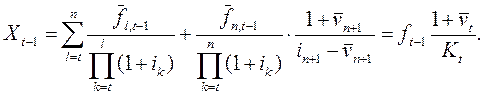          (21.7)

Здесь –– ставка капитализации, определяемая по формуле:

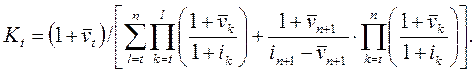           (21.8)

Формула (8) непосредственно обобщает формулу Гордона (21.6) для стационарного постпрогнозного периода на нестационарный прогнозный период. Таким образом, в рамках нашей модели существует линейная зависимость с.в. , которая имеет вид обычной формулы метода прямой капитализации чистого денежного потока:

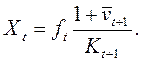                (21.9)

В частности, при  получим из (9) формулу метода прямой капитализации чистого дохода для начальной стоимости актива:

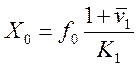                  (21.10)

Здесь –– ставка капитализации чистого денежного потока, которая определяется по формуле (21.8) при  .

Формула (21.10) решает задачу оценки начальной стоимости актива, однако для ее применения необходимо знать ставки дисконта , которые является внешними параметрами модели и должны определяться отдельно. Основная цель данной главы – сделать ставки дисконта внутренними параметрами смешанной модели DDM переменного роста и CAPM. В частности, используя основное уравнение модели CAPM для средней доходности актива и определение ставки дисконта, мы собираемся получить в расширенной модели недостающие соотношения для определения ставок дисконта и сделать смешанную модель замкнутой. С практической точки зрения удобно представить основные соотношения смешанной модели рекуррентными уравнениями, позволяющими использовать для расчета основных характеристик конечные итерационные алгоритмы. В частности, впервые (по нашим сведениям) будет получено рекуррентное уравнение для ставки капитализации, граничное условие для которого дает формула Гордона (21.6).

21.2. Рекуррентное уравнение для ставки капитализации

По определению ставки дисконта  справедливо равенство, которое в принятых нами обозначениях можно записать в виде:

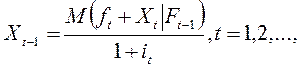            (21.11)

Из (21.11) при сделанных предположениях относительно изменения  получим: