Исследование электрической цепи. Временной и частотный анализ динамики электрических цепей, страница 2

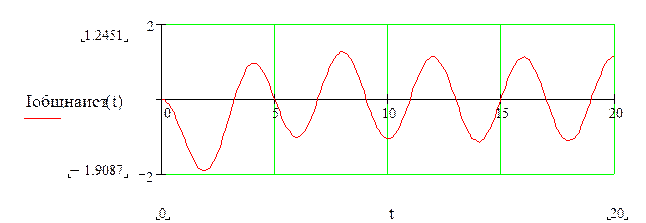
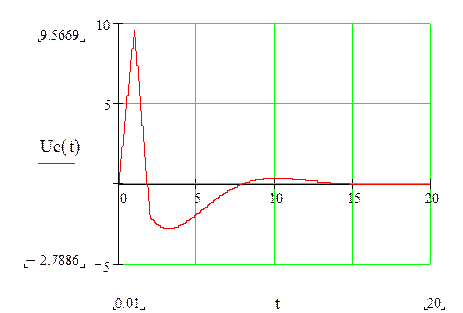
По этому выражению строим график

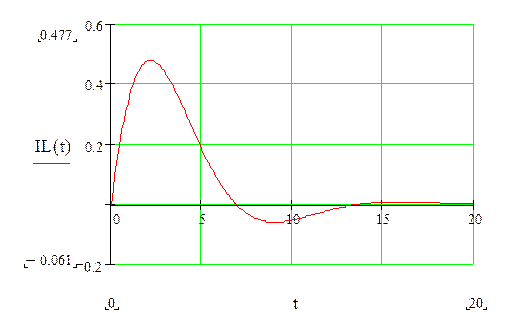
Составляем систему уравнений для нахождения свободной составляющей напряжения на конденсаторе:

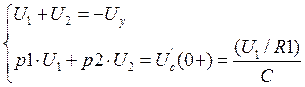
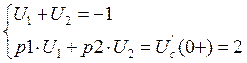
Решаем ее матричным способом в системе MathCAD:

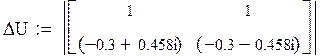
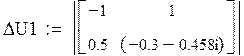
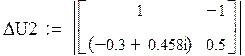
Известно, что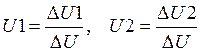

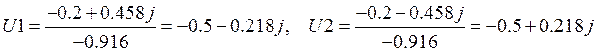
Составляем уравнение зависимости напряжения от времени на конденсаторе, при подачи ступеньки (переходная характеристика цепи):

По этому выражению строим график

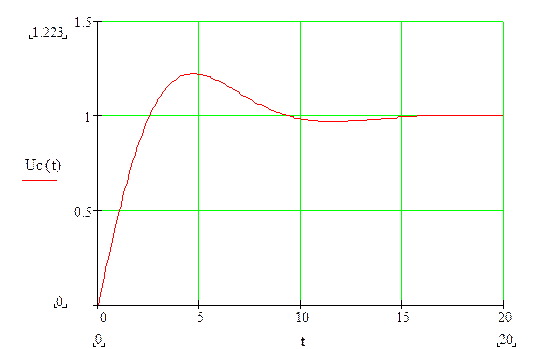
Находим ток на источнике:

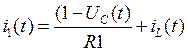
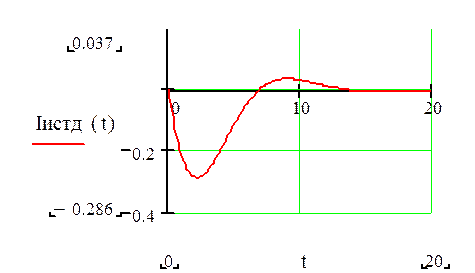
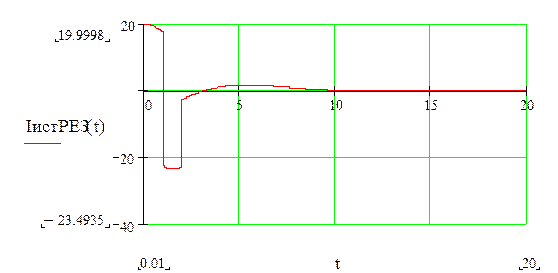
Строим график тока на источнике:

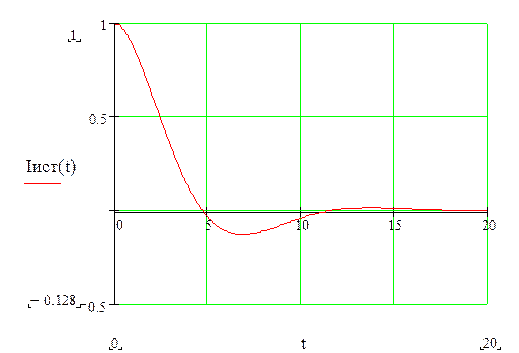
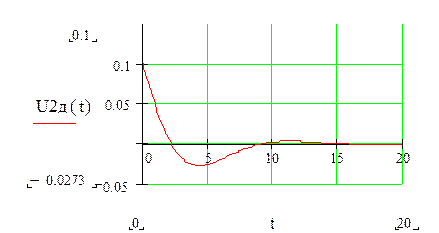
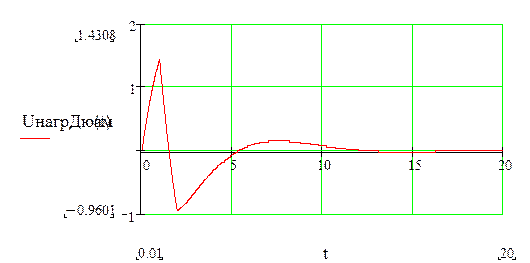
Строим график напряжения на нагрузке:

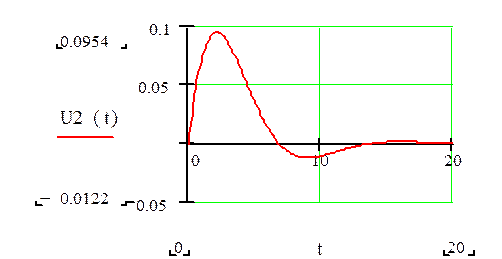
Как видно этот график полностью идентичен с графиком построенным в пакете прикладных програм Math lab, стр. 9, следовательно, расчет выполнен верно.

Реакция цепи на линейный сигнал

Для этого нужно взять интеграл от переходной характеристики:

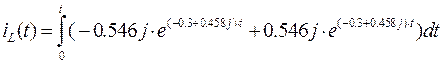
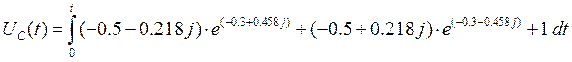
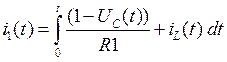
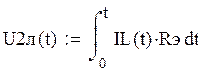
: Строим графики реакции на линейный сигнал

Реакция на дельта-функцию

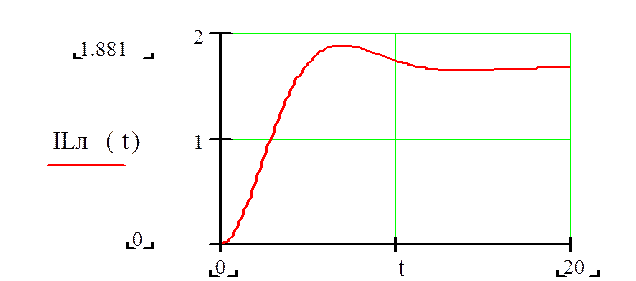
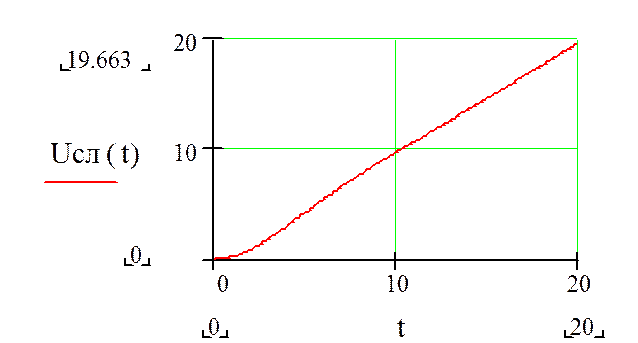
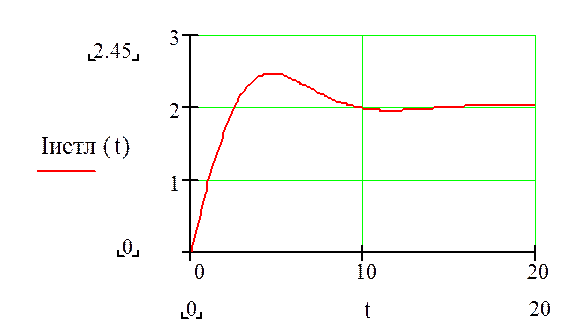
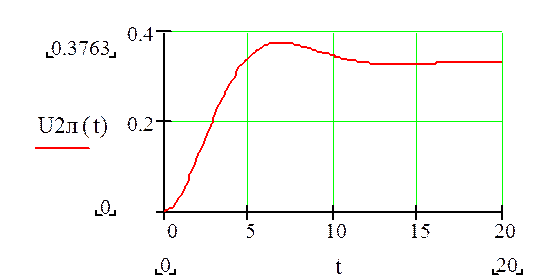
Для этого продифференцируем переходную характеристику:

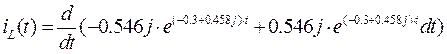
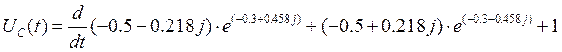
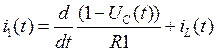
Строим графики реакции на дельта-функцию:

Реакция на синусоидальную функцию

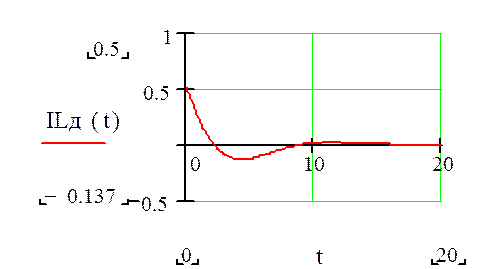
Находим входное сопротивление схемы:

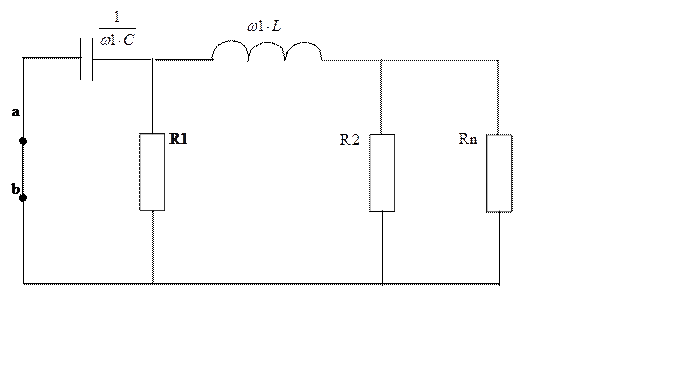
Находим частоту, и входное сопротивление цепи:

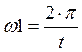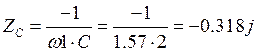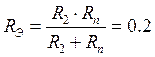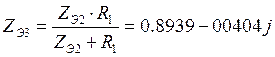, ,   рад/сек,  Ом,  Ом, , Ом,  Ом, Ом.

Ток через источник будет равен:

.

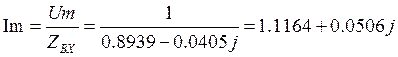Найдем свободную составляющую тока на источнике:

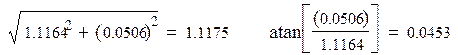 , следовательно

Определение принужденной составляющей тока на источнике:

,

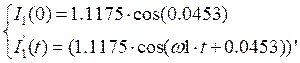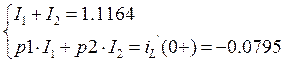
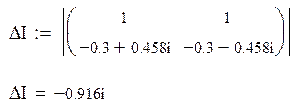
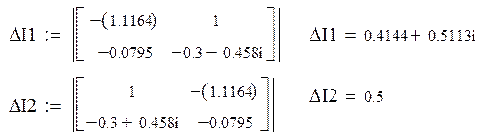
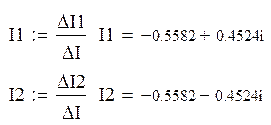
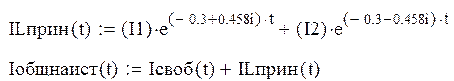
Строим график тока на катушке:

Находим свободную составляющую тока на катушке:

Ток через катушку будет равен:

,

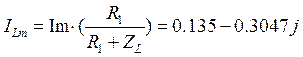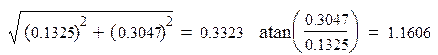 ,следовательно

Определение принужденной составляющей тока на катушке:

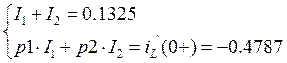
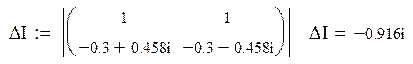
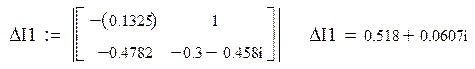
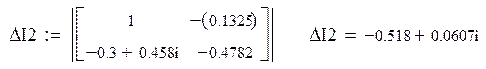
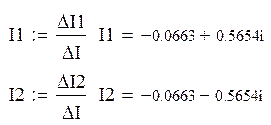
Ток на катушке будет равен:

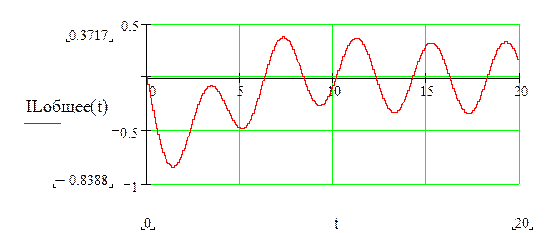
Ток на нагрузке будет равен:

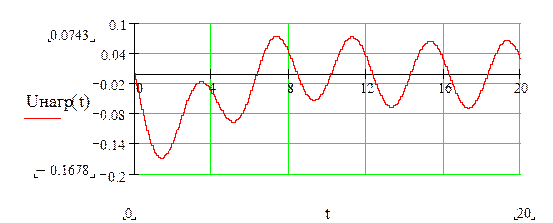
Найдем свободную составляющую напряжения на конденсаторе:

Напряжение на конденсаторе будет равно:

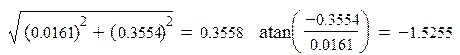, следовательно

Определение принужденной составляющей напряжения не конденсаторе:

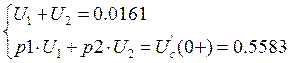
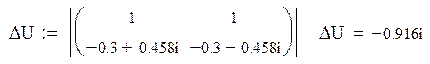
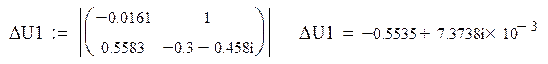
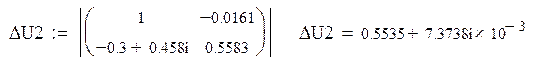
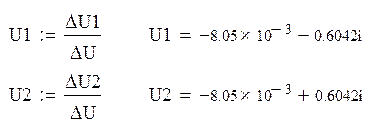
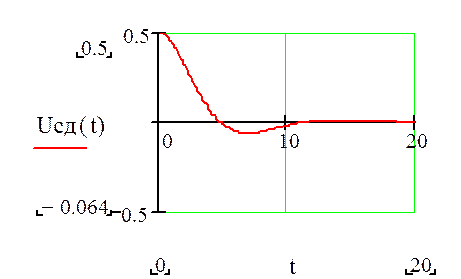
Строим график напряжения на конденсаторе:

Определение реакции цепи с помощью интеграла Дюамеля

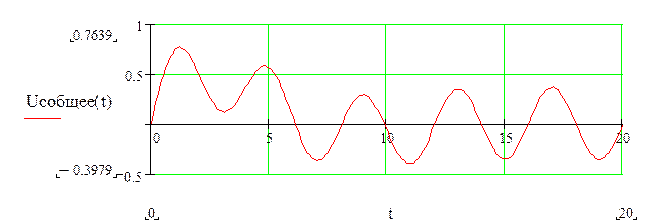
Записываем интеграл Дюамеля для импульса представленного в задании:

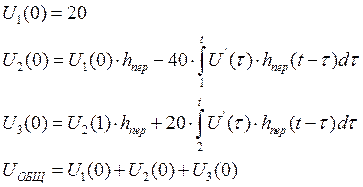
Таким образом реакция на сигнал может быть представлена в виде суммы элементарных сигналов:

Изменение тока на катушке в первый момент времени:

Изменение тока на катушке при t>1:

 

Изменение тока на катушке при t>2:

Результирующий ток протекающий в катушке:

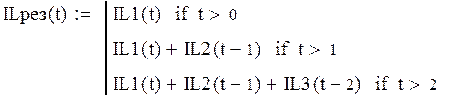
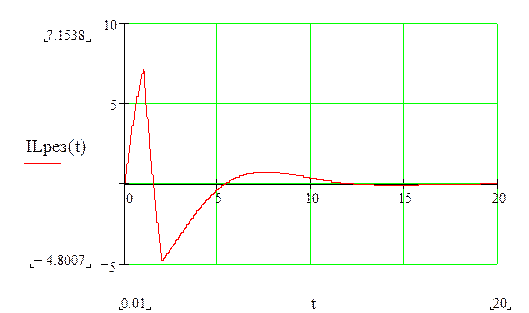
Изменение напряжения на конденсаторе в первый момент времени:

Изменение напряжения на конденсаторе при t>1:

Изменение напряжения на конденсаторе при t>2:

Результирующее напряжение на конденсаторе:

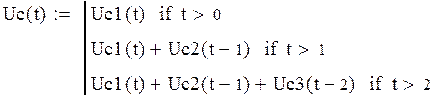
Изменение тока на источнике в первый момент времени:

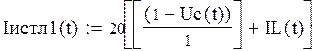
Изменение тока источнике при t>1:

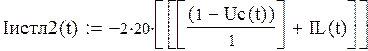
Изменение тока на катушке при t>2:

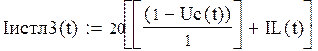
Результирующий ток протекающий на источнике:

Часть 2. Анализ цепи в частотной области описания сигналов и систем

Нахождение операторных коэффициентов передачи и реакции цепи на заданные сигналы

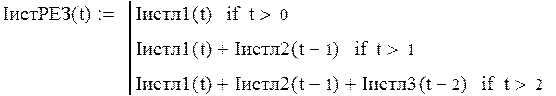
Для нахождения коэффициентов передачи найдем контурные токи в цепи по законам Кирхгоффа

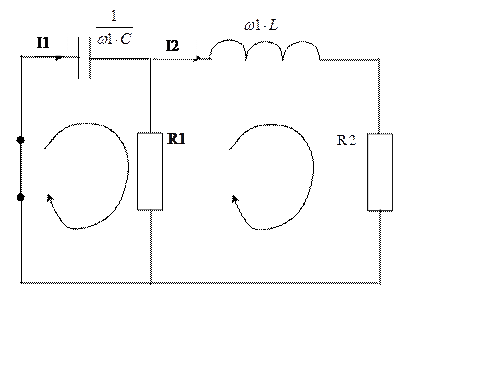
где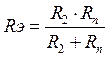

Составляем уравнения:

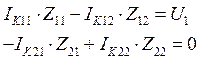
Если считать, что входное напряжение равно единице, то получим:

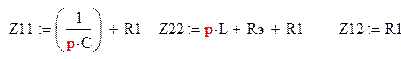
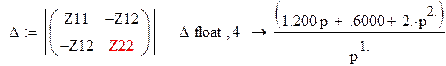
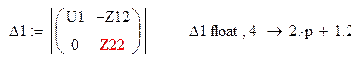
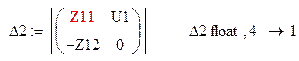
Ток в первом контуре равен:

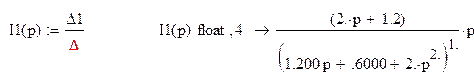
Ток во втором контуре равен:

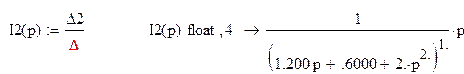
Так как ток во втором контуре равен току в Rэ то можно найти напряжение на Rэ, т.е. , помножив ток I2 на сопротивление Rэ

 

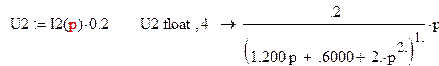
Теперь найдем операторный коэффициент передачи (коэффициент усиления по напряжению)

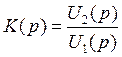, но , следовательно K(p)=U2.

Найдем импульсный коэффициент по напряжению, он равен оригиналу операторного, и представляет собой реакцию цепи на единичный импульс – дельта функцию – и характеризует свободный режим цепи.

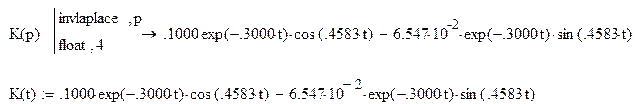
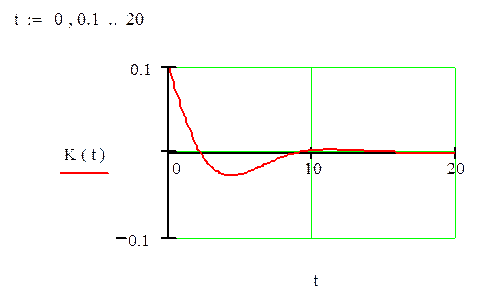
Как видно график полностью совпадает с графиком реакции на дельта функцию из первой части стр.18.

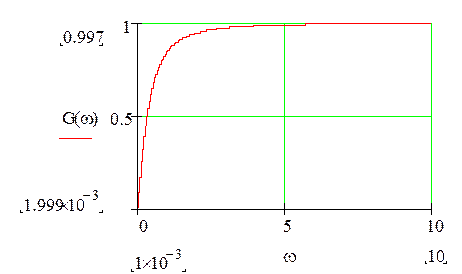
Переходной коэффициент передачи K1(t) представляет собой реакцию на еденичную ступень 1(t), и может быть вычислен как оригинал операторного выражения:

 ,

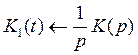В нашем случае:

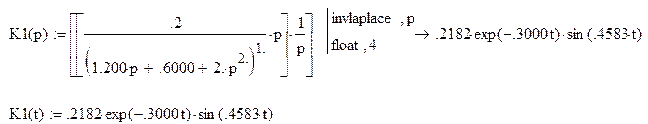
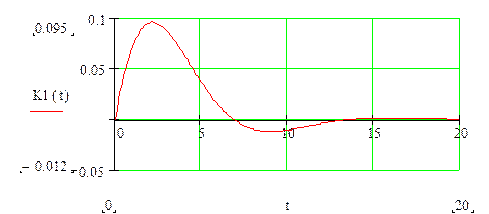
Полученный результат может быть проверен с помощью теорем о начальном и конечном значении функции.

 

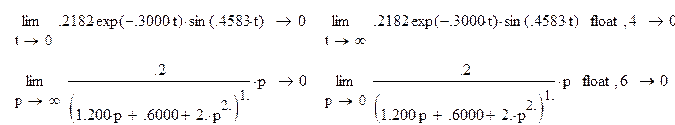
Операторный коэффициент передачи на линейно возрастающую функцию будет равен:

;

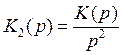коэффициент передачи на линейно возрастающую функцию будет равен оригиналу этого выражения:

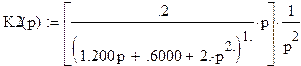
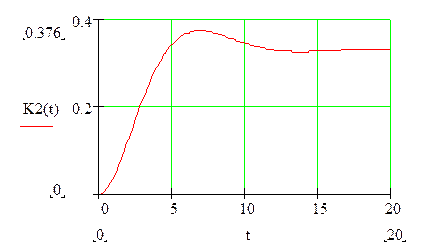
Определяем реакцию цепи на заданный сигнал с помощью интеграла Дюамеля:

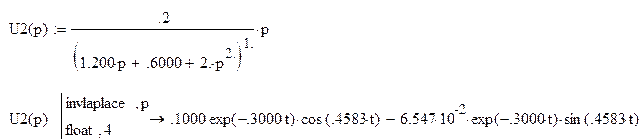
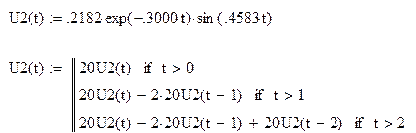
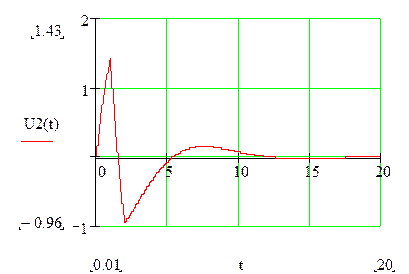
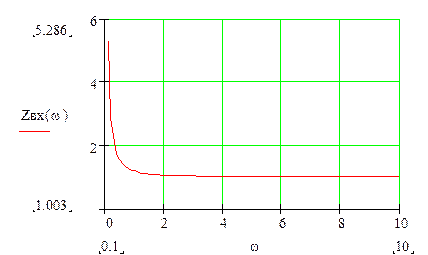
Строим график для входной характеристики – это зависимость входной проводимости от частоты ().

Амплитудно - фазочастотная характеристика цепи

Амплитудно - фазочастотная характеристика цепи получается из операторного коэффициента передачи путем подстановки вместо p   j.

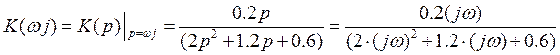
Для того чтобы построить годограф, создаем в Math Lab m-файл и пишем в нем программу:

w=0:0.0001:1.8;

Kwj=(0.2.*(i*w)./(2.*(i*w).^2+1.2.*(w*i)+0.6));

Kim=imag(Kwj);

Kre=real(Kwj);

plot(Kre,Kim)

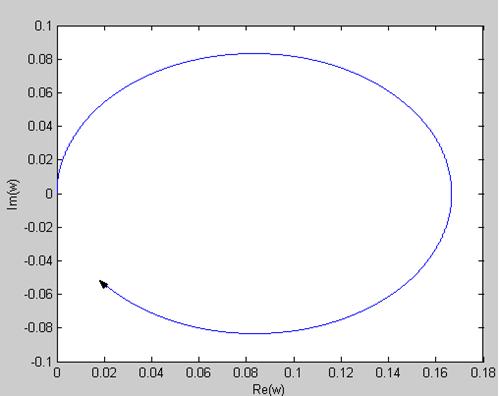
Амплитудно – частотная характеристика:

w=0:0.001:20;

Kwj=(0.2.*(i*w)./(2.*(i*w).^2+1.2.*(w*i)+0.6));

Kw=real(Kwj);

plot(w,Kw)

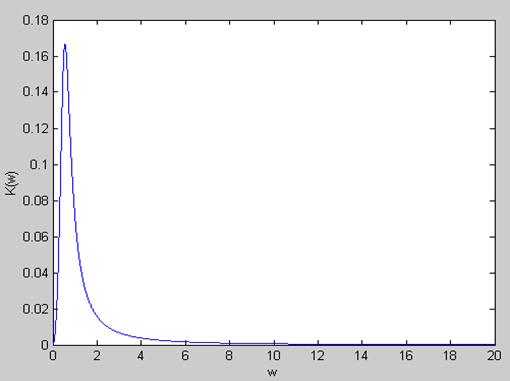
Фазочастотная характеристика:

w=0:0.001:20;

Kwj=(0.2.*(i*w)./(2.*(i*w).^2+1.2.*(w*i)+0.6));

Kf=angle(Kwj);

Kf=(angle(Kwj))/0.017;

plot(w,Kf)

Построение спектра выходного сигнала

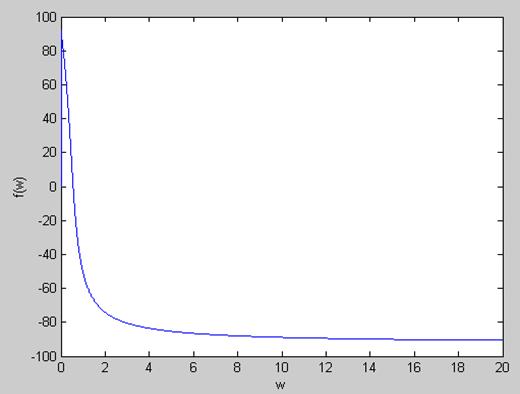
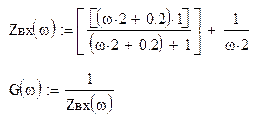
Спектр получается из операторного выражения U₁(p) путем подстановки  вместо p

;

Запишем операторное выражение для входного сигнала:

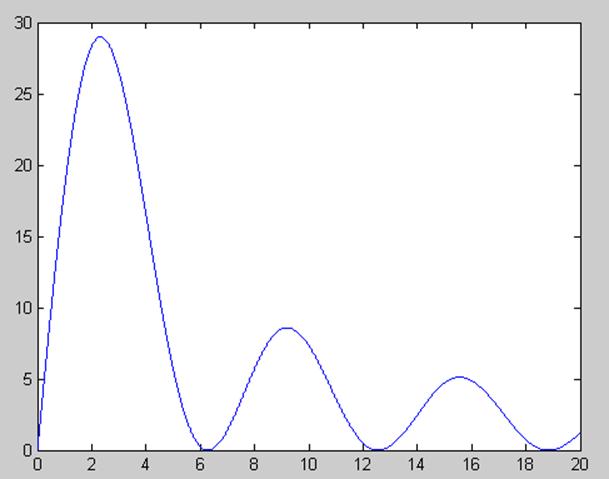
Для построение спектра входного сигнала находим модуль и строим график в программе Math Lab, пример программы для построения спектра приведен ниже:

w=0:0.001:20;

I=(20./w*i).*(1-2.*exp(-w*i)+exp(-2*w*i));

U1=(abs(I));

plot(w,U1)

Для построения спектра выходного сигнала помножим на ,

 

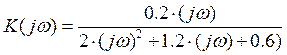
Для построение спектра выходного сигнала находим модуль , умнажаем на и строим график в программе Math Lab, пример программы для построения спектра приведен ниже:

w=0:0.001:20;

I=(20./w*i).*(1-2.*exp(-w*i)+exp(-2*w*i));

U1=(abs(I));

K=0.2.*(w*i)./(2.*(w*i).^2+1.2.*(w*i)+0.6);

K1=abs(K);

U2=K1.*U1;

plot(w,U2)

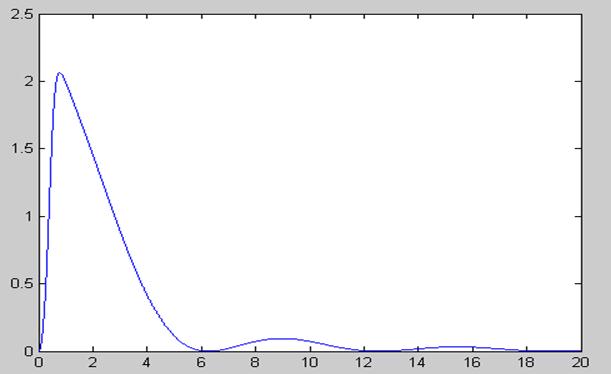
Для сравнения спектра входного и выходного сигнала строим оба спектра сигнала на одном графике:

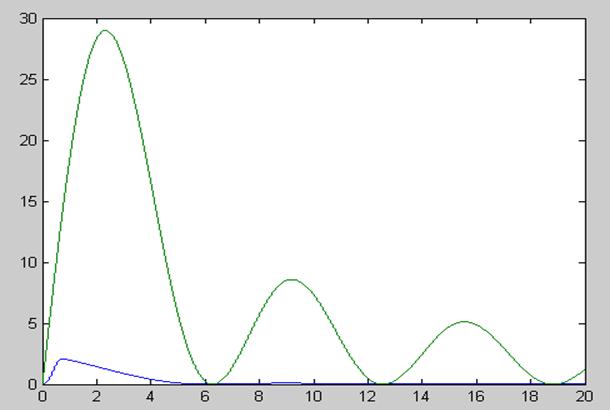
Из спектра графика можно судить, что цепь является фильтром нижних частот, так как высшие гармоники сильно зарезаны, хотя и основная гармоника зарезана в более чем десять раз.

Вывод

Сравнивая результаты, полученные двумя различными методами, можно увидеть, что реакция цепи U₂(t) на импульс напряжения U₁(t) совпадает при расчете двумя различными методами. Данная цепь является фильтром низких частот, зарезая частоты выше , но и при  сильно ослабляет входной сигнал.