![]() ,
(4)
,
(4)
при ограничениях
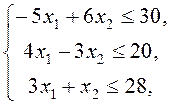
![]() .
(5)
.
(5)
Решение.
Найдем множество ![]() решений неравенств. Для этого
построим три прямые:
решений неравенств. Для этого
построим три прямые:
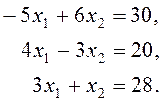
![]()
Прямая ![]() разбивает
плоскость на две полуплоскости. Стрелочками отметим ту полуплоскости, которая
удовлетворяет неравенству
разбивает
плоскость на две полуплоскости. Стрелочками отметим ту полуплоскости, которая
удовлетворяет неравенству ![]() . Для этого достаточно
проверить хотя бы одну точку этой полуплоскости, например, начало координат
. Для этого достаточно
проверить хотя бы одну точку этой полуплоскости, например, начало координат ![]() . Пересечение полуплоскостей составит
множество допустимых решений задачи D.
. Пересечение полуплоскостей составит
множество допустимых решений задачи D.
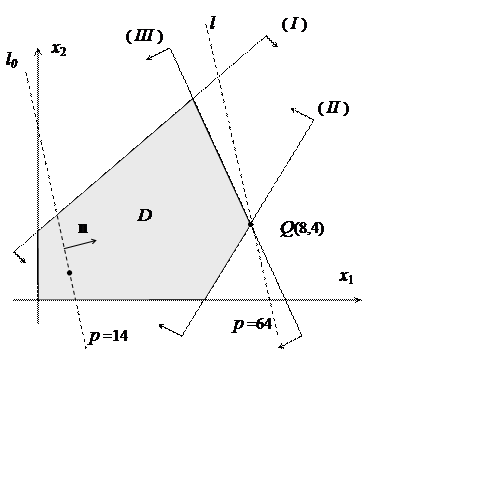 Построим теперь
линии уровня функции F, т.е прямые
Построим теперь
линии уровня функции F, т.е прямые ![]() для различных p.
На рисунке показана прямая, соответствующая значению
для различных p.
На рисунке показана прямая, соответствующая значению ![]() .
На части этой прямой, лежащей внутри этой области, значение функции F равно 14.
.
На части этой прямой, лежащей внутри этой области, значение функции F равно 14.
Параллельно
переместим эту прямую в направлении вектора ![]() . Свое наибольшее
на множестве
. Свое наибольшее
на множестве ![]() значение функция F
примет в вершине многоугольника точке
значение функция F
примет в вершине многоугольника точке ![]() . Для
того чтобы найти ее координаты достаточно решить систему уравнений:
. Для
того чтобы найти ее координаты достаточно решить систему уравнений:
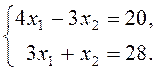
Откуда мы
находим ![]() ,
, ![]() . Итак, максимальное
на множестве
. Итак, максимальное
на множестве ![]() значение функции F равно
значение функции F равно ![]() , которое она принимает в точке с
координатами
, которое она принимает в точке с
координатами ![]() ,
, ![]() .
.
Определение 4. Задача линейного программирования называется канонической, если она имеет следующий вид.
Задача 2. Найти минимум линейной функции:
![]() , (6)
, (6)
при ограничениях
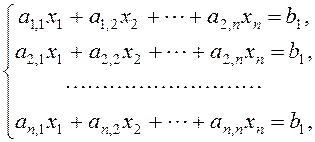 (7)
(7)
![]() ,
,
или в матричной форме
![]() ,
(8)
,
(8)
![]() ,
,
![]() .
(9)
.
(9)
Определение 5. Мы будем говорить, что задача линейного программирования (1,2) сведена к некоторой канонической задаче линейного программирования (возможно с другим числом переменных и ограничений), если по решению первой задачи можно построить решение второй задачи и наоборот.
Пример 4. Свести задачу линейного программирования
![]() , при ограничениях
, при ограничениях
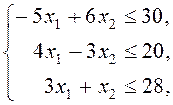 (10)
(10)
![]() , к канонической задаче.
, к канонической задаче.
Перенесем члены неравенств в одну часть так, чтобы полученные выражения были неотрицательны:
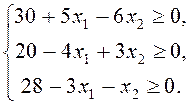
Введем дополнительные
переменные ![]() ,
, ![]() ,
, ![]() по формулам:
по формулам:
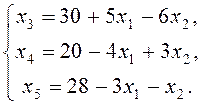 (11)
(11)
Таким образом,
каждому решению ![]() системы неравенств (10) будет
соответствовать решение
системы неравенств (10) будет
соответствовать решение ![]() системы уравнений (11),
причем все его компоненты будут неотрицательны. И наоборот каждому
неотрицательному решению
системы уравнений (11),
причем все его компоненты будут неотрицательны. И наоборот каждому
неотрицательному решению ![]() системы (11) будет
соответствовать решение
системы (11) будет
соответствовать решение ![]() системы (10).
системы (10).
Если функция F принимает в некоторой точке
максимальное значение, то в этой точке функция (–F)
принимает свое минимальное значение. Причем эти значения будут равны с точностью
до знака. Таким образом, вместо максимума функции ![]() на
множестве D можно искать на
этом множестве минимум функции
на
множестве D можно искать на
этом множестве минимум функции ![]() .
.
Таким образом, искомая задача может быть сведена к следующей задаче линейного программирования:
![]() , при ограничениях
, при ограничениях
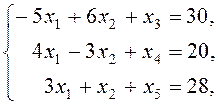
![]() .
.
По оптимальному решению первоначальной задачи легко найти оптимальное решение канонической задачи.
Минимальное значение функции ![]() , в точке с
координатами:
, в точке с
координатами:
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Определение 6. Набор из m различных переменных системы уравнений (7) называется базисным, если все переменные из этого набора могут быть выражены только через оставшиеся переменные с помощью элементарных преобразований системы. Переменные, входящие в этот набор, называются базисными, а остальные свободными.
Определение 7. Решение системы (7) называется базисным (опорным планом), если значения всех свободных переменных равны нулю.
Пример 5. Найти базисное решение системы:
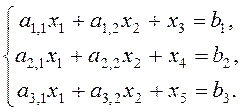 (12)
(12)
Решение.
В этой системе уравнений за базисные переменные можно взять переменные ![]() , а за свободные
, а за свободные ![]() ,
так как первые легко выражаются через последние. Итак, базисным решением этой
системы будет набор чисел
,
так как первые легко выражаются через последние. Итак, базисным решением этой
системы будет набор чисел ![]() .
.
Определение 8. Симплекс-таблицей для канонической задачи (6), (7) называется следующая таблица:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.