Табличное представление задачи ЛП, симплекс-таблица. Симплекс-метод для отыскания опорного решения задачи ЛП

Этот факт хорошо иллюстрируется геометрическим представлением данной задачи на рисунке 2.5.

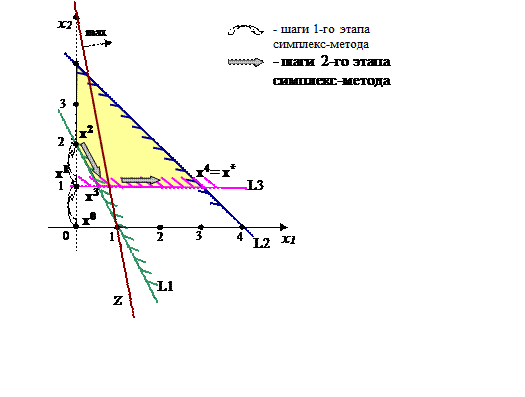
Рисунок 2.5 – Геометрическая иллюстрация решения задачи ЛП из примера 2.5

1.1.2. Симплекс-метод для отыскания опорного решения задачи ЛП

Симплекс-метод для решения задачи ЛП состоит из двух основных этапов. Первый этап предназначен для отыскания опорного допустимого  решения (или установления факта несовместности ограничений, т.е. того факта, что задача не имеет ни одного допустимого решения). Второй этап состоит из последовательного перехода от полученной на первом этапе точки к другой точке, для которой целевая функция имеет большее значение, до получения точки, соответствующей оптимальному решению.

Описание первого этапа симплекс-метода

Рассмотрим первый этап симплекс-метода.

Пусть в таблице вида (2.12) все свободные члены неотрицательны, т.е.  b₁ ≥ 0, …, b_m ≥  0. В этом случае таблица вида (2.12) дает возможность сразу получить одно из допустимых опорных решений задачи (2.4) и можно считать, что первый этап выполнен.

Теперь предположим, что в таблице вида (2.12) есть хотя бы один отрицательный свободный член, например, пусть  b _{i 0} < 0. В этом случае точка (x,y), определяемая данной симплекс-таблицей, соответствует недопустимому решению, так как  у _{i 0} = b _{i 0} < 0.

Симплекс-метод для отыскания допустимого опорного решения означает специальное правило перехода от данной точки  Р₀ = (x,y) к такой соседней, которую отделяет от выпуклого многогранника D (являющегося множеством допустимых решений исходной задачи) меньшее (во всяком случае не большее) число гиперплоскостей, т.е. для которой в соответствующей таблице содержится меньшее (не большее) число отрицательных свободных членов.

Для осуществления перехода от вершины  Р₀ = (x,y) к указанной соседней производим шаг жорданова исключения, выбирая разрешающий элемент согласно ПРАВИЛУ 1. После конечного числа шагов либо установим несовместность системы ограничений, либо перейдем к таблице, не содержащей отрицательных свободных членов, т.е. получим допустимое опорное решение задачи, приравняв нулю все независимые переменные, оказавшиеся на верху таблицы.

ПРАВИЛО 1 выбора разрешающего элемента

Примечание 3. В случае вырождения, когда 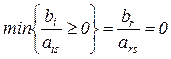 , элемент  a_rs  выбираем  в качестве разрешающего лишь в том случае, если при  a_rs >0 .

Пример 2.5 (продолжение)

Рассмотрим таблицу, соответствующую итерации 1 примера 2.5, полученную выше:

Так как y₁ = -2 < 0 и y3 = -1 < 0, то точка (x,y)⁰ = (0; 0; - 2; +4; - 1), определяемая данной таблицей, соответствует недопустимому решению. Поэтому необходимо произвести переход к другой точке с помощью модифицированного жорданова исключения. Разрешающий элемент выбираем по правилу 1. а именно: в первой строке (так как b₁ = -2 по абсолютной величине больше b₃ = -1) отыскиваем любой отрицательный коэффициент, например, a₁₂ = -1, поэтому 2-ой столбец объявляем разрешающим. Теперь рассчитаем неотрицательные симплексные отношения:      b₁ : a₁₂ = (-2) : (-1) = 2 > 0,     b₂ : a₂₂ = 4 : 1 = 4 > 0,      b₃ : a₃₂ = (-1) : (-1) = 1 > 0. минимальное из них соответствует 3-ей строке, а, следовательно, 3-я строка объявляется разрешающей. При  этом элемент a₃₂ будет разрешающим элементом.

Переходим к следующей 2-ой итерации.

Эта таблица определяет точку (x, y)¹ = (0; 1; -1; 3; 0)    (или точку x¹  = (0;1) ). Эта точка соответствует  решению, которое также является недопустимым, так как y₁ = -1 < 0. Поэтому переходим к следующей точке, т.е. к следующей таблице. Разрешающий элемент a₁₂ = - 1.

Эта таблица определяет точку (x, y)² = (0; 2; 0; 2; 1)    (или точку x²  = (0;2) ).  Полученная точка соответствует допустимому решению, так как в соответствующей таблице все свободные члены b_i   положительны.

1.1.3. Симплекс-метод для отыскания оптимального решения  ЗЛП

Описание второго этапа симплекс-метода

Пусть в результате выполнения первого этапа симплекс-метода получена следующая таблица:

После нескольких шагов жордановых исключений на верх таблицы перешло (m-l) зависимых переменных  y_i , а слева от таблицы появилось (n-k)переменных  x_j; очевидно, что  m-l = n-k.   Так как первый этап симплекс-метода выполнен, в таблице вида