Примеры решения задач по дисциплине "Высшая математика", страница 3

тис А означат, что рассматриваемый экземпляр — бракованный. Заметим, что „0.018182.события В,, 132 и В, образуют полную группу событий. По условию, Р(В1) = ().5,

 По формуле

Из этоГо кугв«та надо сделать такой же вывод, как из замечания после предыду-что взятый наугад экземпляр выпущен на первом щет примера: лучше к экзамену вопросы учить, а не рассчитывать на то, чтоБейеса вероятность того, станке, при условии, что он бракованный, равна удастся хорошо ответить экспромтом.

Приведённых формул и классического определения вероятности достаточно для решения большого класса задач, некоторые из которых разбиракпся в следующих примерах.

Аналомчнб

ПРИМЕР

В первом ящике находится 2 белых и 5 чёрных шаров, а во втором 4 белых и З чёрных. Из первого ящика наугад вытаскивают шар, кладут его во торой,

15

14

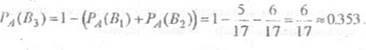
ПРИМЕР З.

 Некоего театрала постигло несчастье он потерял процтаммку с репертуаром местных театров на •гекчщиЙ сезон. 110 лрциции, каждое воскресенье он ходит в театр на спектакль, стараясь подобрать новый для себя. Положившись на волю случая. он решил поехать в титр на первом подошедшем автобусе. Автобус первого маршрута подойдет с вероятностью 0.2 и отвезёт его к первому лсатру, второй — с вероягностью 0.45 — ко второму театру и третий — с вероятностью 035 - в третий теајр. Вероятность того, что в театре сегодня идет новый спектакль. составляет 0.3 для первого театра. 0.2 для второго и 0.4 — для трегьето театра. Какова вероятность того, что театрал всё же попадет на новый

спектакль?

        Решение                                                                                                                                               

Опять воспользуемся формујюй полной вероятности. Полную группу событий составлякп Вь В) и Вз- означающие приход первым автобуса первого, второго и третьего маршрута соответственно- Вероятности этих событий по условию равны ().2, 0.45 и 0.35 соответственно. Пусть событие А также означает 30, что театрал посетит новый спектакль. По условию, РА (А ) = 03, РЛ (А) 0.2 и Рв, (А ) = 04 , так что искомая вероятность принимает значение

Геометрическое определение вероятности.

Несмотря на 10, что классическое определение вероятности позволяет решать достаточно широкий класс задач, надо заметить, что оно становится совершенно неприменимо в тех случаях, когда число элементарных исходов бесконечно. В этих случаях также не имеет смысла поиск вчюяпюсгей событий, заключающихся в одном конкретном исходе. Понятно, что вероятность такого события всегда будет равна нуло. В таких случаях мы будем рассматривать события, заключающиеся в том, что результат испытания принадлежит какому-то подмножеству элементарных исходов.

Такие задачи могут быть сведены посредством отопествления множества элементарных исходов множеству точек некоторй ограниченной фигуры (отрезка, области, тела) к следующей задаче.

Пусть имеется некоторая ограниченная фигура G и в ней содержится другая фигура g. В фигуру С.; наудачу помещается точка. Спрашивается, чему равна вероятность Р того, что точка попадет в g. При этом фраза «наудачу помещастся точка» имеет следующий смысл: точка может попасть в любую точку

16

фтуры причем вероятность ее попадания в какую-то часть этой фигуры пропорциональна „мерс этой части (длине для отрезка, площади для области, объёму для лела) и пс зависит сп формы и расположения •лой части.

Таким образом, по определению,  попадания в фијуру g при помещении наудачу точки в фшуру (Э равна Р = упу_Щ, mes (Э где mes g обозначает меру (длину, ПЛОЩЩЏ, и т.д.) фигуры g. Такое определение 1 јазывают геометрическим опреДелениел вероятности.

ПРИМЕР 1 (Задача о встрече)

Двое договорились встретиться с 1.3^w до 14^W в извесзном им месте. По дотворенности, каждый из них ждет другого не более 20 минут. Какова вероятность того, •гго встреча всё-таки произойдет, если каждый из них независимо

другого может прийти с равной вероятностью в любой момент времени с 13оо до 14⁰⁰?

Решение

Пусть время прихода первого товарища а, а время прихода второго — Ь. Оба значения измеряјся•ся в часах. Нам известно только, что ae[13, 14], и эти величины независимы. Таким образом, можно считать, что исходом испытания является пара вещественных чисел а и Ь. Сопосмавим множеству всех исходов точки на декартовой плоскости, координат которых х = а — 13 и у = Ь - 13 удовлтворяют условию Очевидно, эти точки образуют квадрат, изображенный на рис. 2а. Множество благоприятных исхо-

дов описывается неравенством        . Эл» неравенство эквивалентно системе

из двух неравенств

x-ys-, з   з

1

                                          з              з

Эгой системе неравенст соответствует заштрихованная область на рис. 26.

1

                    о                     о

                                              а)                                     6)

Рис. 2. Иллюстращш к примеру 1.