









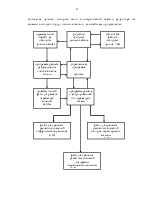



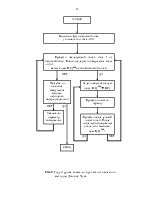


3.3 АЛГОРИТМ ЧИСЛЕННОГО РЕШЕНИЯ СИСТЕМЫ ИНТЕГРАЛЬНЫХ УРАВНЕНИЙ ГАЛЛЕНОВСКОГО ТИПА, СТРУКТУРНАЯ СХЕМА ПРОГРАММЫ.
3.3.1. Общий подход к решению системы интегральных уравнений Галленовского типа.
Полученные в разделе 3.2 интегральные уравнения являются интегральными уравнениями Фредгольма первого рода. Символически эти уравнения можно записать следующим образом:
![]() (42)
(42)
где Z – линейный интегральный оператор;
![]() -
искомая функция тока;
-
искомая функция тока;
J(s) – известная функция, определяемая условиями возбуждения.
Решение уравнений Фредгольма первого рода является очень сложной задачей. Для решения задач такого рода используют численные методы решения.
Область
определения оператора Z,
то есть система функций, на которую данный оператор действует, назовем
пространством ![]() . Систему функций,
порождаемых оператором Zпри его действии на любой элемент
. Систему функций,
порождаемых оператором Zпри его действии на любой элемент ![]() , назовем
пространством
, назовем
пространством ![]() . Будем считать, что
пространства
. Будем считать, что
пространства ![]() и
и ![]() являются
гильбертовыми с нормами, определяемыми скалярным произведениями:
являются
гильбертовыми с нормами, определяемыми скалярным произведениями:
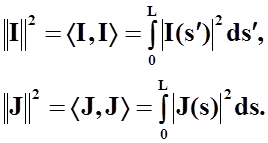
Среди
численных методов отыскания решений интегральных уравнений наиболее общим
является проекционный метод или метод моментов. Предположим, что мы знаем две
системы координатных функций ![]() и
и ![]() , являющихся базисами введенных
пространств
, являющихся базисами введенных
пространств ![]() и
и ![]() ,
такими, что любую функцию из пространств
,
такими, что любую функцию из пространств ![]() и
и ![]() , согласно введенной норме, можно
представить как линейную комбинацию координатных функций.
, согласно введенной норме, можно
представить как линейную комбинацию координатных функций.
Приближенное
решение уравнения (42)будем искать в виде суммы функций ![]() , называемых базисными:
, называемых базисными:
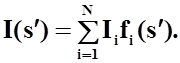 (43)
(43)
Комплексные
коэффициенты ![]() подлежат определению. Подставив
(43)в(42) получим:
подлежат определению. Подставив
(43)в(42) получим:
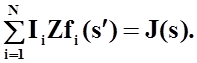 (44)
(44)
Коэффициенты
![]() найдем из условия минимума нормы
невязки ( разности между левой и правой частями ) этого уравнения. Для этого
необходимо и достаточно, чтобы невязка была ортогональна ко всем функциям
найдем из условия минимума нормы
невязки ( разности между левой и правой частями ) этого уравнения. Для этого
необходимо и достаточно, чтобы невязка была ортогональна ко всем функциям ![]() , которые называются проекционными.
Для отыскания приближенного решения количество проекционных функций выберем
конечным. Таким образом, получаем:
, которые называются проекционными.
Для отыскания приближенного решения количество проекционных функций выберем
конечным. Таким образом, получаем:
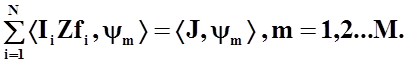 (45)
(45)
Часто
выбираетсяM=N,
однако при использовании уравнений Галленовского типа, когда в интегральные
уравнения включены дополнительные неизвестные коэффициенты, получается M>N. Соотношение (45) представляет собой систему линейных
алгебраических уравнений относительно неизвестных коэффициентов разложения ![]() , которую можно представить в
матричной форме:
, которую можно представить в
матричной форме:
![]() (46)
(46)
Считая, что базисные и проекционные функции являются вещественными элементами матрицы [K] , запишем в виде интегралов:
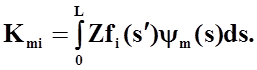
Правая часть системы линейных алгебраических уравнений (46) представляет собой вектор-столбец с компонентами:
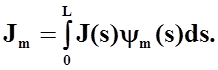
Матрицу коэффициентов и свободные члены в полученной системе уравнений в общем случае необходимо рассчитывать численным интегрированием. Естественно, что при этом требуемый объем вычислений и достаточная точность решения определяется как видом базисных и проекционных функций, так и видом ядра используемого интегрального уравнения.
Решение
интегрального уравнения Фредгольма первого рода относится к классу некорректных
задач в том смысле, что небольшие изменения в правой части ![]() могут привести к значительным
изменениям решения. Неустойчивость задачи может проявиться в том, что возникнет
система линейных алгебраических уравнений с плохо обусловленной матрицей.
могут привести к значительным
изменениям решения. Неустойчивость задачи может проявиться в том, что возникнет
система линейных алгебраических уравнений с плохо обусловленной матрицей.
Решение некорректных задач требует специальных приемов – так называемых методов регуляризации решения. Существует много методов регуляризации решения, подробно они изложены в [2]. Однако при аккуратной формулировке рассматриваемых задач «автоматически» работает так называемый метод саморегуляции [1]. Он состоит в том, что для точного ядра, имеющего логарифмическую особенность, или для приближенного ядра при малом радиусе проводника диагональные элементы матрицы системы линейных алгебраических уравнений преобладают над остальными. Такие матрицы имеют достаточную обусловленность. Обусловленность матрицы определяется [2]:
![]()
если cond(A)>>1 , матрицу называют плохо обусловленной. В противном случае – хорошо обусловленной. В этом случае особое значение приобретает высокая точность вычисления элементов матрицы и уменьшение ее размерности.
3.3.2 Выбор проекционных и базисных функций. Обоснование выбора вида интегрального уравнения.
Выбор базисных и проекционных функций, сказывающихся на размерности задачи, точности вычисления элементов матрицы системы линейных алгебраических уравнений, затратах машинного времени, в значительной мере определяет качество вычислительного алгоритма.
В качестве проекционных функций могут использоваться различные системы линейно-независимых функций. Принято выделять несколько канонических случаев [1]. Так, если функции определяются таким образом:
![]()
то такой метод принято называть методом наименьших квадратов. Если обе координатные последовательности совпадают друг с другом:
![]()
то такой метод принято называть методом Бубнова-Галеркина. В качестве проекционных функций могут быть выбраны дельта-функции Дирака, то есть:
![]()
Этот метод называется по
Л. В. Контаровичу – метод коллокации, или согласование в точках. Такой выбор
проекционных функций равносилен требованию обращений в нуль невязки в
фиксированных точках ![]() .
.
Основным
недостатком первых двух методов является в общем случае необходимость в
вычислении двойных интегралов по переменным ![]() .
Метод коллокации проще в вычислительном отношении, так как лишен отмеченного
недостатка.
.
Метод коллокации проще в вычислительном отношении, так как лишен отмеченного
недостатка.
Выбор той или иной системы проекционных функций, определяющий последующую схему вычислительного процесса, должен быть согласован с видом интегрального уравнения. Численное решение уравнения Поклингтона, основанное на методе коллокации, дает крайне медленную сходимость решений. В основном это объясняется неадекватным описанием в уравнении быстро меняющегося поля в близи источника возбуждения. Поэтому при решении уравнения Поклингтона необходимо использовать процедуру Бубнова-Галеркина, обеспечивающую лучшую сходимость по сравнению с методом коллокации [3].
Другой подход к электродинамическому анализу тонких проводников основан на интегральном уравнении Мея, которое получено на основе рассмотрения электродинамических потенциалов, и, в частном случае прямолинейного проводника, принимает вид уравнения Галлена. Уравнение Мея успешно решается методом согласования в точках, причем имеет следующие особенности:
![]() хорошая сходимость наблюдается
практически независимо от вида базисных функций;
хорошая сходимость наблюдается
практически независимо от вида базисных функций;
![]() правая часть уравнения представляет
собой гладкую функцию даже при сосредоточенном возбуждении проводника, что
делает решение не критичным к выбору модели возбуждения излучателя;
правая часть уравнения представляет
собой гладкую функцию даже при сосредоточенном возбуждении проводника, что
делает решение не критичным к выбору модели возбуждения излучателя;
![]() сравнение систем уравнений,
возникающих при численном решении уравнения Мея (методом согласования в точках
) и уравнения Поклингтона ( метод Бубнова-Галеркина ), показывает, что обусловленность
соответствующих матриц в первом случае значительно лучше.
сравнение систем уравнений,
возникающих при численном решении уравнения Мея (методом согласования в точках
) и уравнения Поклингтона ( метод Бубнова-Галеркина ), показывает, что обусловленность
соответствующих матриц в первом случае значительно лучше.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.