Выражения для передаточных функций разомкнутой и замкнутой систем

Задание: По заданному нулю и пяти полюсам передаточной функции записать выражения для передаточных функций разомкнутой и замкнутой систем. Найти дифференциальное уравнение системы. Нарисовать структурную схему. Найти и построить АЧХ, ФЧХ, АФХ разомкнутой системы. Найти весовую и передаточную функцию разомкнутой системы. Проанализировать устойчивость работы системы методами Рауса-Гурвица, Михайлова, Найквиста. Построить графики ЛАЧХ, ЛФЧХ разомкнутой системы. Построить асимптотическую ЛАЧХ. Определить устойчивость работы системы по ЛАЧХ и ЛФЧХ.

K
300	-3	-0,3	0	0	-0,2	-100

1.1 Выражение передаточной функции разомкнутой системы

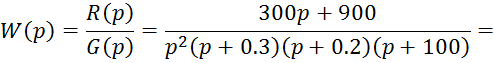
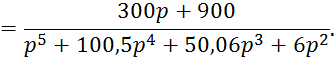
1.2 Выражение передаточной функции замкнутой системы

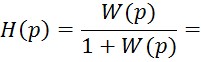
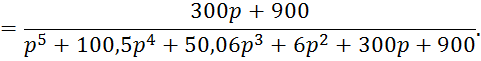
2.1 Дифференциальное уравнение разомкнутой системы

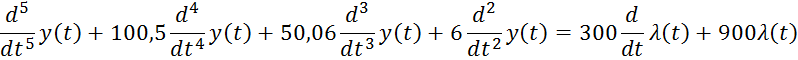
2.2 Дифференциальное уравнение замкнутой системы

(

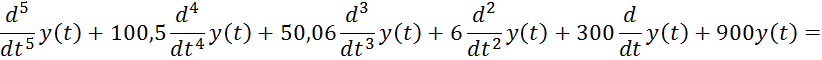
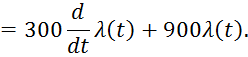
3 Структурная схема

Изобразим структурную схему разомкнутой системы исходя и её передаточной функции:

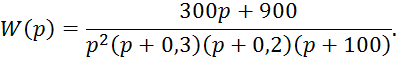
Рис.1 Структурная схема

4 АЧХ, ФЧХ, АФХ разомкнутой системы

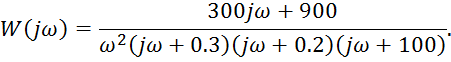
АЧХ:

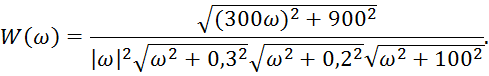
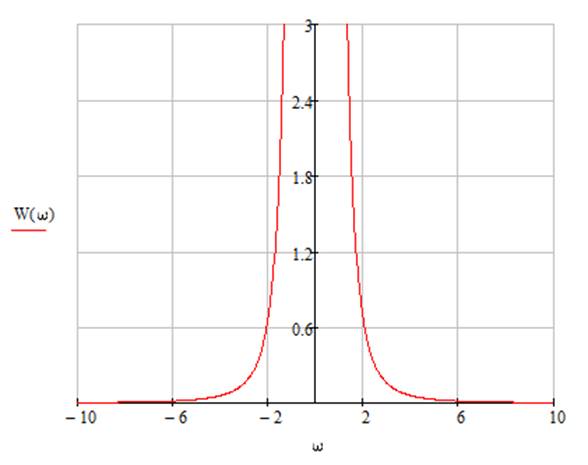
Рис.2 АЧХ

ФЧХ:

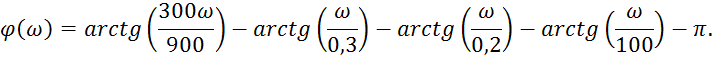
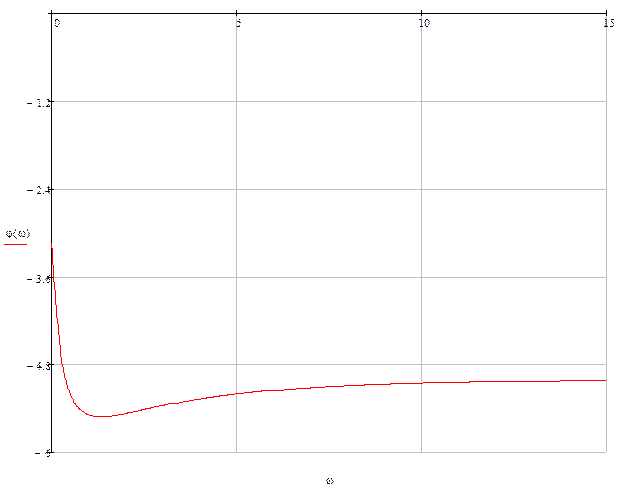
Рис.3 ФЧХ.

АФХ:                               

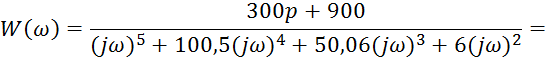
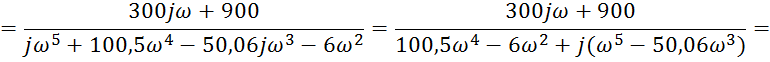
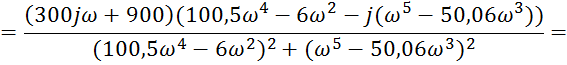
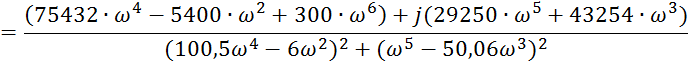
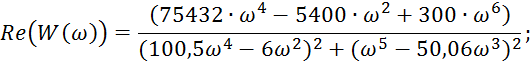
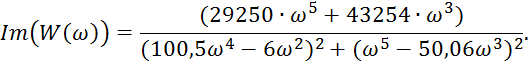
Построим АФХ разомкнутой системы:

:

Рис.4 АФХ разомкнутой системы.

5 Весовая и переходная функции разомкнутой системы

Переходная функция находится как обратное преобразование Лапласа:

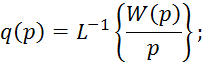
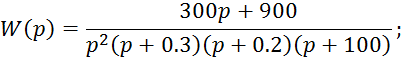
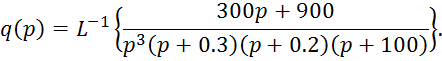
Окончательное выражение для переходной функции:

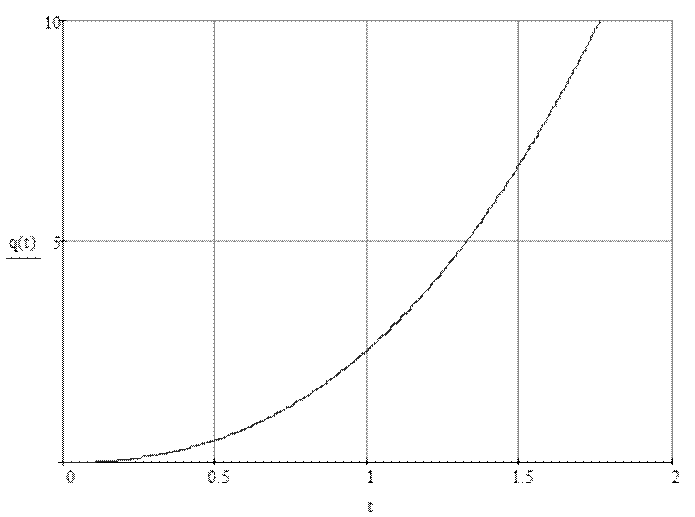
Рис.5 Переходная характеристика.

Весовая функция находится как производная от переходной функции по времени:

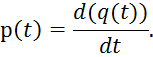
Окончательное выражение для весовой функции:

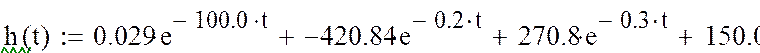
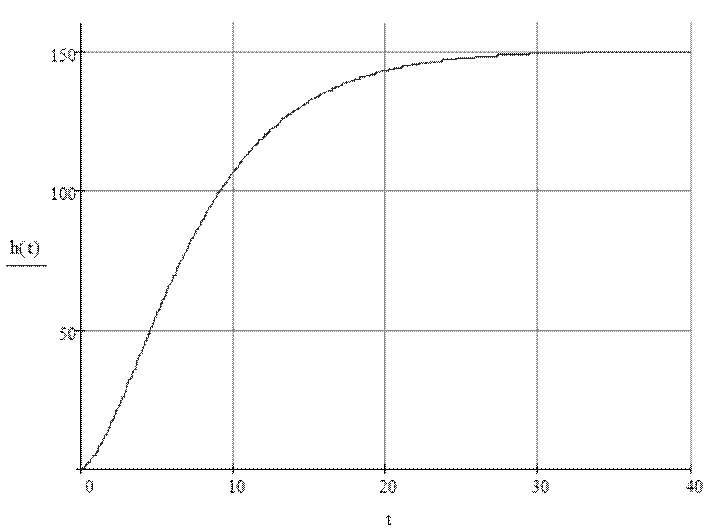
Рис.6 Весовая функция.

6 Анализ устойчивости работы замкнутой системы

6.1Критерий Рауса-Гурвица

Критерий Гурвица:

Для того, чтобы САУ была устойчива, необходимо и достаточно, чтобы все определители Гурвица имели знаки, одинаковые со знаком первого коэффициента характеристического уравнения .

Для этого запишем уравнение для замкнутой САУ:

Из которого найдём коэффициенты:

И составим определители Гурвица:

Так как третий, четвёртый и пятый определители имеют отличный от  знак, значит что система неустойчива.

6.2 Критерий Михайлова

Для того чтобы САУ была устойчива, необходимо и достаточно, чтобы Годограф Михайлова при изменении частоты от нуля до бесконечности, начинаясь при  на вещественной положительной полуоси, обходила только против часовой стрелки последовательно n квадратов координатной плоскости, где n - порядок характеристического уравнения.

Характеристическое уравнение для замкнутой САУ имеет вид:

Положив , выделим действительную и мнимую части характеристического полинома:

Годографом Михайлова является зависимость мнимой части характеристического полинома от его действительной части:

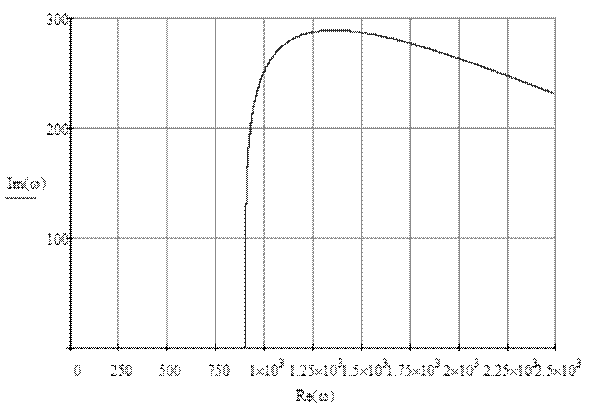
Рис.7 Годограф Михайлова при .

Рис.8 Годограф Михайлова при .

,

Рис.9 Годограф Михайлова при .

Т.к. Годограф Михайлова не обходит поочерёдно против часовой стрелки все квадранты, то из этого можно сделать вывод о неустойчивости системы.

6.3 Критерий Найквиста

Для того чтобы САУ была устойчива, необходимо и достаточно, чтобы АФХ разомкнутой системы при изменении частоты от нуля до бесконечности не охватывала точку с координатой (-1,).

АФХ разомкнутой системы:

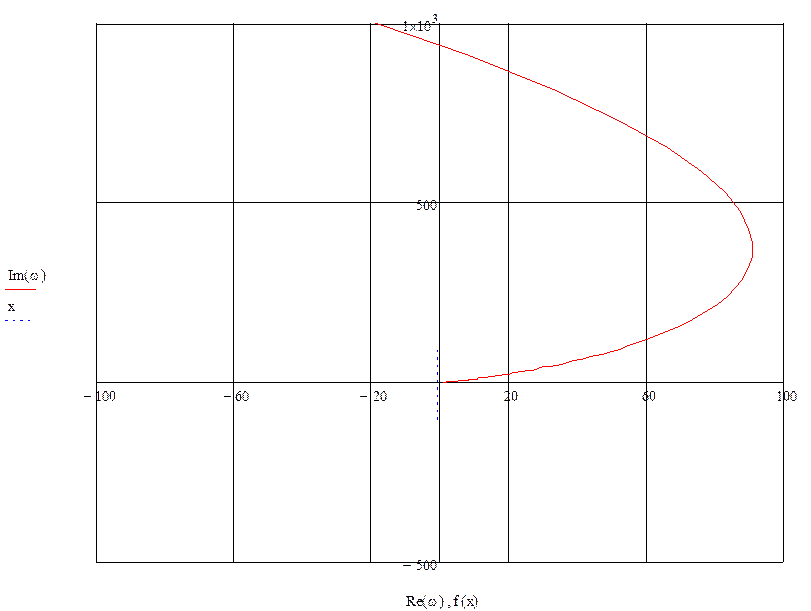
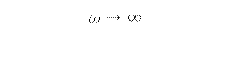
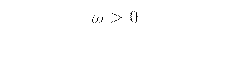
Рис.10 АФХ разомкнутой системы.

При  АФХ стремится к нулю.

Из графика видно, что кривая АФХ охватывает точку с координатой (-1,), из чего следует, что система неустойчива.

7 ЛАЧХ, ЛФЧХ, асимптотическая ЛАЧХ

Анализ устойчивости разомкнутой системы по ЛАЧХ и ЛФЧХ.

Для анализа устойчивости системы с помощью ЛАЧХ  и ЛФЧХ, необходимо определить резонансную частоту и частоту среза. Если частота среза больше значения резонансной частоты, то система будет являться неустойчивой.

ЛАЧХ:

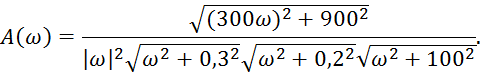
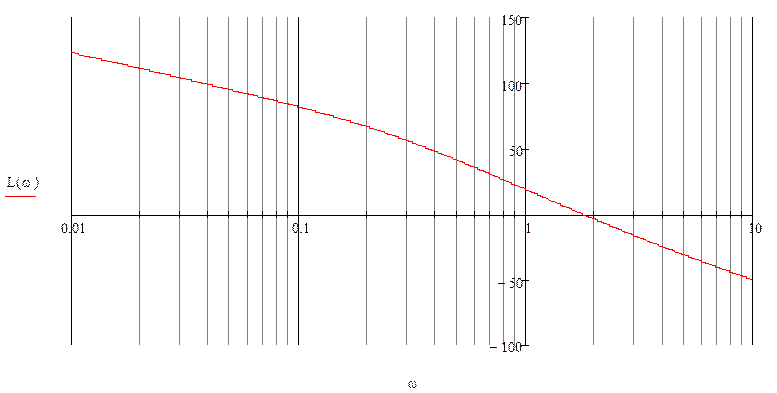
Рис.11 ЛАЧХ

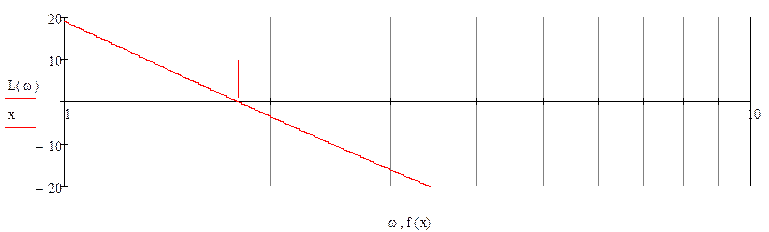
Частотой среза будет та частота, при которой график ЛАЧХ пересекает 0.

ЛФЧХ:

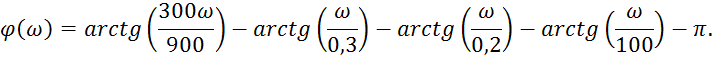
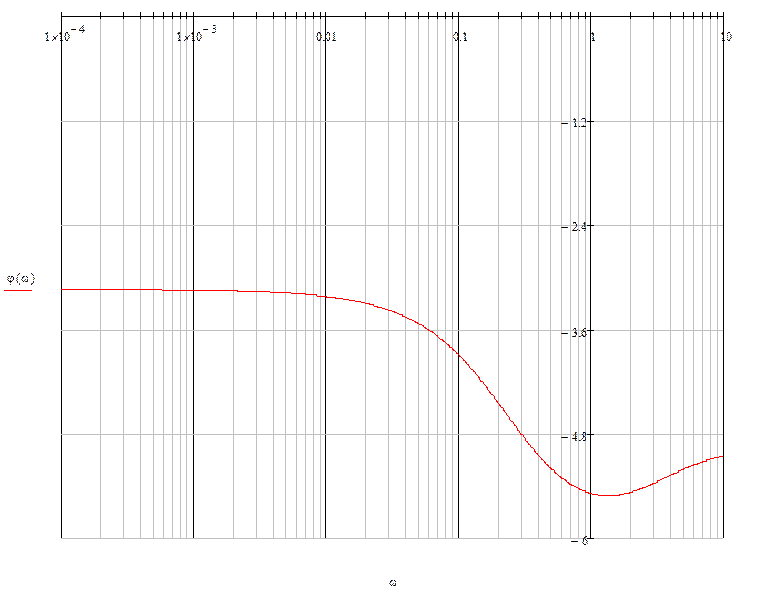
Рис.12 ЛФЧХ.

Из графика ЛАЧХ видно, что резонансная частота бесконечно близка к нулю, что меньше частоты среза, а значит система неустойчива.

Асимптотическая ЛАЧХ

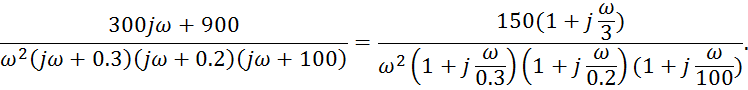
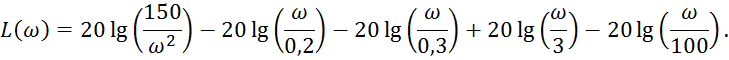
Рис.13 АЛАЧХ.

Вывод: В данной работе была исследована заданная система.

Были построены частотные характеристики системы и переходные характеристики.

Система была проанализирована на устойчивость по методикам Рауса-Гурвица, Михайлова и Найквиста, а так же по логарифмическим частотным характеристикам.

Все методики дали один и тот же результат, система является неустойчивой.