Функции многих переменных. Общие определения. Координатное пространство

случае, когда определитель формы (4) не равен 0, но эта форма не является определенной, стационарная точка  не будет точкой экстремума.

Продолжение примера 1. Вернемся к функции  . Мы нашли стационарную точку . Вычислим второй дифференциал в этой точке:

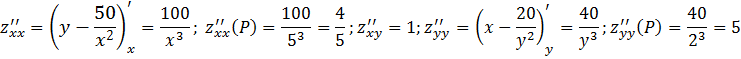
и . Это положительно определенная форма, ибо  и  . Следовательно,  -- локальный минимум. Мы знаем большее :  -- глобальный минимум в области .  Без исследования функции  на границе области , нельзя получить этот факт.

Пример 2. Найти экстремумы функции трех переменных . Частные производные  приравниваем к нулю и находим восемь стационарных точек . Так как второй дифференциал  имеет диагональный вид, то он будет положительно определен если,  и отрицательно определен, если  Следовательно, (2,1,3) – локальный минимум, а  -- локальный максимум. В остальных стационарных точках экстремума нет.

9  Условный экстремум

Пусть нам задана функция двух переменных , которую мы будем называть целевой, а также задано уравнение связи

которое на плоскости Оху задает кривую  Требуется найти локальные экстремумы (максимумы и минимумы) функции  на кривой . Точка , удовлетворяющая уравнению связи (1),  называется локальным условным максимумом  (минимумом) функции , если  найдется окрестность  этой точки такая, что  для любой точки , лежащей на кривой т.е. удовлетворяющей  условию связи (1).

Например, поставим задачу вычисления наибольшего и наименьшего значений функции  при условии связи . Геометрически это значит, что на окружности радиуса  с центром в начале координат мы ищем наибольшее и наименьшее значения функции . В данном случае задачу нетрудно свести к поиску экстремумов функции одной переменной. Действительно, заданная окружность описывается параметрически как ,  и экстремум функция

достигает при значении параметра, удовлетворяющем соотношению

Отсюда либо  , либо . Тем самым либо  либо .  Значение функции  в первой точке  равно 5, а во второй -5. Это и будут наибольшее и наименьшее значения, так как по теореме Вейерштрасса  на окружности, как на ограниченном и замкнутом множестве, любая непрерывная функция достигает своего наибольшего и наименьшего значения в точках  и .  По теореме Ферма, соответствующие им значения  параметра удовлетворяют (2) и тем самым , а

Однако, задать параметрически и тем более разрешить уравнение (1) относительно одной из переменных не всегда удается. Как найти условный экстремум в этом случае? Предположим, что    -- условный экстремум целевой функции  сравнением связи (1). Предположим также, что у нас имеется  теоретическая возможность выразить    через  из уравнения (1) в окрестности точки  в виде    . Тогда  -- локальный экстремум функции   , поэтому, по необходимому условию экстремума имеем:

Кроме того, дифференцируя по  соотношение  находим:

Умножим (4) на неопределённый множитель  λ   и сложим с (3). Получим:

Подберём  λ   так, что выражение   было бы  равно нулю (Заметим, что условие  вместе с непрерывностью частных производных является достаточным для разрешения уравнения (1) относительно ).  Тогда и оставшаяся часть тоже должна быть 0. Получим систему:

Вместе с уравнением связи эта система задает  необходимое условие условного локального экстремума.  Все три уравнения (5) и (1) можно записать единым образом, если рассмотреть функцию Лагранжа    и записать для неё необходимое условие безусловного экстремума:

Первые два уравнения в (6) совпадают с (5), а последнее есть не что иное, как уравнение связи(1).

Описанный выше метод поиска условного экстремума называется методом множителей Лагранжа. В общем случае он формулируется так. Пусть надо найти условный экстремум функции  на множестве точек  удовлетворяющем уравнениям связи

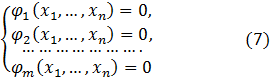
При этом точка  называется условным локальным максимумом (минимумом), если найдется окрестность  этой точки такая, что  (соответственно ) для любого набора , удовлетворяющего соотношениям (7).  Составляем функцию Лагранжа

Теорема. Если  -- условный локальный экстремум функции  при условии (7), то найдутся значения множителей Лагранжа  такие, что

Замечание. Если из уравнений связи все неизвестные можно выразить через одну, скажем   , то задача о условном экстремуме сводится к задаче поиска