Теория функций комплексного переменного. Поле комплексных чисел

1  Поле комплексных чисел

Алгебраической причиной введения комплексных чисел является отсутствие действительного корня уравнения . В самом деле,  для любого действительного , причем лишь если . Но именно это обстоятельство позволяет расширить область действительных чисел  до поля комплексных чисел  

Комплексное число имеет вид , где  -- вещественные числа, называемые действительной и мнимой частью комплексного числа z (записываем так: ), а  -- новое число, называемое комплексной единицей  и обладающее свойством .  Два комплексных числа равны в том и только том случае,  когда совпадают их действительные и мнимые части.  Операции сложения и умножения над комплексными числами определяются следующим образом

 (1)

Нулевое комплексное число  нейтрально по отношению к сложению (т.е.  для всех ), а единица  нейтрально по отношению к умножению.  Противоположное комплексное число  обладает тем свойством, что .  Прямым способом проверяются свойства  ассоциативности и  коммутативности сложения и умножения,  а также дистрибутивность умножения относительно сложения:

Заметим, что равенство  следует из определения (1), а именно

.

Здесь и далее мы отождествляем комплексное число  с действительным числом . Возможность такого отождествления обосновывается тем, что

Заметим, что в этих равенствах знаки сложения и умножения использованы в двух смыслах: как сложение (умножение) действительных чисел  и  и как  сложение (умножение)  двух комплексных числе   и  согласно определению (1).

Если то либо , либо  , и поэтому . В этом случае комплексное число  имеет обратное

Действительно,

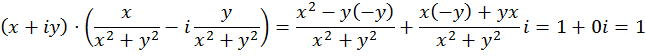
Тем самым совокупность всех комплексных чисел превращается в поле. Поле действительных чисел изоморфно вкладывается в поле   посредством отображения , как это уже было отмечено в равенствах (2).

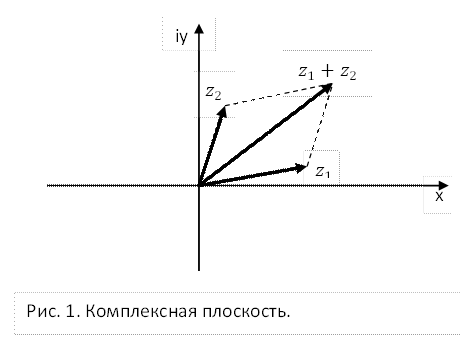Комплексные числа изображаются точками на плоскости Oxy или векторами с начальной точкой в начале координат (см. рис. 1). Горизонтальная ось Ox называется действительной осью, а вертикальная ось Oy называется мнимой осью и обозначается как  ибо по ней откладываются чисто мнимые числа  и.т.д..  При этом сложение двух комплексных чисел можно рассматривать как сложение двух векторов по правилу параллелограмма. Геометрическая интерпретация умножения будет указана позже.

Примеры. А. 

Б.

В. 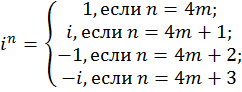. В частности .

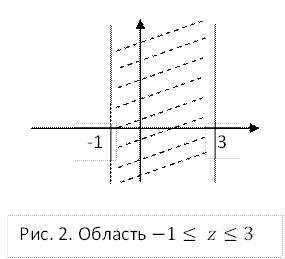Г. Нарисуем область комплексных чисел , удовлетворяющих неравенствам . Ответ см. на рис. 2.

2  Сопряжение комплексных чисел

Комплексное число  называется комплексно сопряженным к , а отображение  называется сопряжением. Сопряжение является биективным отображением комплексной плоскости на себя. С геометрической точки зрения операция сопряжение есть не что иное, как  отражение относительно действительной оси.

Равенство  имеет место тогда и только тогда, когда z – действительное число. Кроме этого, сопряжение обладает свойством гомоморфности по отношению к сложению и умножению:

Эти свойства проверяются непосредственно. Как и всякая симметрия, сопряжение обладает свойством инволютивности:   для любого .

Отметим также свойство  , которое приводит к следующему правилу деления комплексных чисел: для того, чтобы разделить одно комплексное число на другое надо числитель и знаменатель дроби умножить на величину сопряженную знаменателю (см. пример Б, §1).

3  Тригонометрическая форма записи комплексных чисел

Изобразим комплексное число  вектором.  Длина этого вектора, т.е. величина  называется модулем комплексного числа  и обозначается . Если  -- действительное число, то приходим к «школьному»  модулю, ибо . Если , то угол, который образует вектор  с действительной осью называется  аргументом комплексного числа  и обозначается  Пусть  – модуль и аргумент ненулевого комплексного числа. Тогда

 (1)

Выражение называется тригонометрической формой записи комплексного числа.

Свойства модуля.  Для любых комплексных чисел    имеют место соотношения:

а)   ,     б)   (неравенство треугольника);

Докажем первое равенство:

Извлекая квадратный корень, получим равенство . Второе равенство следует из первого, ибо оно эквивалентно следующему соотношению: .

Докажем неравенство треугольника. Обозначая  и возводя в квадрат, заменяем это неравенство на равносильное:

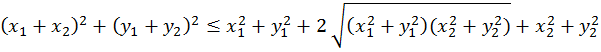
Возводя в квадрат в левой части и сокращая, получаем эквивалентное неравенство

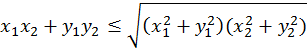
Это неравенство будет следовать из неравенства

которое, после возведения в квадрат и сокращения, превращается в неравенство

Последнее неравенство несомненно верно. □

Следствие. Множество комплексных чисел с единичным модулем (обозначим:   – комплексная единичная окружность) замкнуто относительно умножения и обращения.

Перемножим два комплексных числа в тригонометрической форме записи:

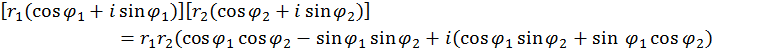
Применяя тригонометрические формулы «косинус суммы» и «синус суммы», приходим к следующему правилу: при перемножении комплексных чисел модули умножаются, а аргументы складываются

(2)

В частности, перемножая число  на себя n раз, получаем  формулу Муавра: