Лабораторная работа 2М
Анализ амплитудного спектра и оценка
среднеквадратического значения сигнала на основе
дискретного преобразования Фурье (ДПФ)
1. Цель работы: Исследование особенностей и возможностей анализа амплитудного спектра на основе ДПФ в задачах определения параметров сигналов, дискретизируемых с помощью быстродействующих АЦП.
2. общие теоретические сведения
Преобразование Фурье -
одна из самых распространенных процедур, применяемых при цифровой обработке сигналов. Дискретизация сигнала приводит к тому, что амплитудный
спектр
сигнала бесконечно повторяется на частотной оси с периодом, равным ![]() =1/Тд. Для того чтобы
дискретизация не привела к потере информации, требуется согласно теореме Котельникова
выбирать интервал дискретизации меньше половины периода наивысшей гармоники
спектра. Математически прямое
и обратное преобразование Фурье для непрерывной функции
=1/Тд. Для того чтобы
дискретизация не привела к потере информации, требуется согласно теореме Котельникова
выбирать интервал дискретизации меньше половины периода наивысшей гармоники
спектра. Математически прямое
и обратное преобразование Фурье для непрерывной функции ![]() определяется
следующими выражениями:
определяется
следующими выражениями:
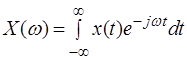 ;
;
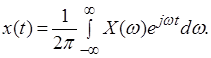
Дискретное преобразование Фурье (ДПФ) отображает дискретные временные последовательности в частотные, и определяются следующим образом:
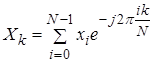 для k = 0,1,2, … , N-1
для k = 0,1,2, … , N-1
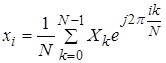 для
i = 0,1,2, … , N-1
для
i = 0,1,2, … , N-1
где x - входная последовательность; X - спектр входной последовательности; N - число выборок в дискретной временной и дискретной частотной областях.
ДПФ формирует дискретный частотный спектр так же, как сигнал во временной области формируется АЦП. Результат ДПФ аналогичен просмотру непрерывного обработанного окном спектра через «штакетник» с щелями в интервалах, соответствующих частотным щелям.
Некоторые свойства ДПФ
1. ДПФ последовательности x приводит к комплексной выходной последовательности X:
F{x} = X = XRe + j XIm = Re{X} + j Im{X}.
Если общее количество выборок N входной последовательности x четно, выходная последовательность X выводится в комплексной форме в формате, представленном в табл. 1. Здесь k = N/2.
Элемент массива |
Интерпретация спектральных компонент сетки частот ДПФ |
|
X0 X1 X2 ….. X k-2 X k-1 Xk = X-k X k+1 = X N-(k-1) = X -(k-1) X k+2 = X N-(k-2) = X -(k-2) ….. XN-3 XN-2 XN-1 |
Нулевой компонент 1-я гармоника (шаг сетки) 2-я гармоника ….. (k-2)-я гармоника (k-1)-я гармоника k-я гармоника (N/2) - (k-1) -я гармоника - (k-2) -я гармоника ….. - 3-я гармоника - 2-я гармоника - 1-я гармоника |
3. Частота и частотный интервал выборки (шаг частотной сетки) определяется через шаг дискретизации следующим образом:
![]() ;
; ![]() ,
,
где N - число выборок в последовательности.
Простой способ увеличить разрешение состоит в том, чтобы увеличить число выборок или увеличить выборочный интервал.
Использование окон
Теорема Котельникова утверждает, что сигнал может быть полностью восстановлен из дискретных, одинаково расположенных отсчетов, если частота выборки по крайней мере вдвое больше самой высокой частоты этого сигнала. Если сигнал не с целым числом периодов в пределах окна выборки, то на границах этого окна будут разрывы, которые приводят к дополнительным спектральным компонентам в частотной области, известные как спектральная утечка или растекание спектра. Для уменьшения дополнительных составляющих спектра принимают специальные меры, основанные на предварительном сглаживании временной последовательности. В частности для минимизации спектральной утечки, выборки данных в начале и конце сигнала сглаживают путем их уменьшения до нуля. Сглаживание временной последовательности заключается в умножении всех отсчетов сигнала на весовые коэффициенты специальной функции, называемой «окном». Разработано большое количество окон, отличающихся по параметрам разрешающей способности, степени сглаживания, влияния на отношение сигнал/шум и т.д.
Наиболее часто при решении практических задач используюся следующие типы окон: Хэмминга (Hamming), Ханна (Hann), Кайзера (Kaiser), Блэкмена (Blackman), Flat Top, - а также комбинированные: Кайзера-Бесселя (Kaiser-Bessel), Блэкмена-Харриса (Blackman-Harris) и др. Известны также окна: гауссово, треугольное, косинусное, Чебышева, Бартлетта-Ханна, Тьюки. Если на последовательность отсчетов не накладывается никакая сглаживающая функция, то такое окно называют прямоугольным (Uniform). Прямоугольное окно эквивалентно отказу от дополнительной обработки временной последовательности, поэтому его целесообразно использовать в случае, когда основные гармонические составляющие анализируемой последовательности совпадают с сеткой частот ДПФ. Прямоугольное окно также целесообразно, когда сигнал представляет собой широкополосный белый шум.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.