Группы гомологий асинхронных систем переходов. Практическое решение задач, страница 2

Лемма 1.1. Отображение, сопоставляющее каждой асинхронной системе  пунктированный полигон , продолжается до функтора из категории  асинхронных систем переходов в категорию пунктированных полигонов.

Доказательство. Каждому морфизму  поставим в соответствие гомоморфизм , определенный на элементах  как  в случае , и  при . Если , то в силу , верно , независимо от того, имеет ли место , ибо  действует на  как тождественное отображение. Отсюда  будет удовлетворять соотношению  и определять морфизм пунктированных полигонов.

2. Группы гомологий асинхронных систем переходов.

Пусть  - произвольный моноид, - правый пунктированный полигон над . Рассмотрим категорию , объектами которой являются элементы , а морфизмами  - такие тройки , что . Композиция морфизмов  равна , ибо . Рассмотрим произвольный функтор  в категорию левых  - модулей над кольцом  с .

Гомологии полигона  с коэффициентами в определим как  - модули гомологий  категории  с коэффициентами в , в смысле [2, Приложение 2]. С этой целью рассмотрим комплекс  - модулей  определим гомоморфизмы , считая, что  при  на слагаемом с индексом  модуля  равен композиции , где  - инъекция слагаемого с индексом , а  при  и  - инъекции  слагаемого с индексом

 . Положим

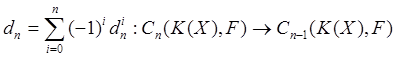 при , и  

Получим комплекс

Модулем -хгомологий будем называть левый  - модуль . В частности . Здесь  обозначает прямой предел (или копредел) функтора в смысле теории категорий.

Пример 2.1. Пусть  пунктированный полигон, принимающий значения

  при  и .

Иными словами, действует на себе посредством правых сдвигов. Тогда для произвольного функтора  принимающего значение  модули гомологий  равны 0 при .

Пространством состояний будем называть асинхронную систему переходов без выделенного начального состояния. Легко видеть, что пространство состояний, с морфизмами, не требующими сохранения начального состояния, составляют категорию, которая будет изоморфна подкатегории категории пунктированных полигонов. Обозначим через  пунктированный полигон, соответствующий пространству состояний .

Определение. Левыми -модулями гомологий  пространства состояний  с коэффициентами в функторе  называются  - модули . В частности .

Пример 2.2. Пусть  - пространство состояний асинхронной системы переходов такой, что . Тогда категория  будет свободной. В этом случае тройки  для которых  будут ребрами графа, который мы обозначим через , имеющего множество вершин . Категория  будет равна категории , морфизмами которой служат ориентированные пути в графе . Обозначим множество его (направленных) ребер через . Пусть  обозначает начало ребра , а  - конец ребра. Потоком на графе  с коэффициентами в  называются семейство  таких элементов , не более чем конечное число из которых равно 0, что для каждой вершины  имеет место равенство . Согласно [3],  будет изоморфен  - модулю потоков на  с коэффициентами в . Хорошо известно, что для свободной категории  модули гомологий  равны 0 при .

Пусть  - произвольный моноид,  - рассматриваемый как функтор правый полигон, определенный по формуле на единственном объекте и сопоставляющий каждому  отображение , где  на  и  на отмеченной точке. Для  любого объекта  категории  определена комма-категория [4]  (или кослой, в терминологии книги [2]), объектами которой служат морфизмы ), а морфизмы  между двумя такими стрелками  и  задаются элементами , удовлетворяющими соотношению .

Лемма 2.1. Категория  для любого , изоморфна категории .

Доказательство. Каждый  определяет  морфизм  правых полигонов над   по формуле . Это дает функтор , обратный к которому определяется с помощью отображения .

Для произвольного моноида ,  пунктированного полигона  и функтора  определим функтор  и действующий на морфизмах  таким образом, что  ограничение  на подмодуле  равно композиции , где  обозначает инъекцию прямого слагаемого. Поскольку этот функтор определен на категории, имеющей единственный объект, то он является правым  -модулем. Следующее ниже утверждение позволяет свести изучение гомологий асинхронных систем к гомологиям моноидов.

Теорема 2.2. Пусть - произвольный моноид,  - пунктированный полигон. Тогда для всех  имеют место изоморфизмы , где  - группы гомологий моноида  с коэффициентами в правом  - модуле .