![]()
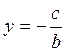
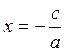
![]()
![]() m
m
![]()
А О у=0 х
Рис.
3.5 Рис. 3.6
Мы
считаем здесь, что ![]() ; если а=0, по условию теоремы
будет
; если а=0, по условию теоремы
будет ![]() и можно взять точку В
и можно взять точку В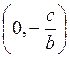 .
.
Пусть
m – прямая, проходящая через точку А перпендикулярно
вектору ![]() . Ее уравнение можно найти по точке А и
нормальному вектору
. Ее уравнение можно найти по точке А и
нормальному вектору ![]() :
: 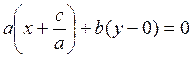 ,
откуда после упрощений
,
откуда после упрощений ![]() .
.
Таким
образом, уравнение линии ![]() и уравнение прямой m
совпадают. Тем самым доказано, что
и уравнение прямой m
совпадают. Тем самым доказано, что ![]() есть прямая и что
вектор
есть прямая и что
вектор ![]() - ее нормальный вектор.
- ее нормальный вектор.
Так
как ![]() , то
, то ![]() и
следовательно,
и
следовательно, ![]() - направляющий вектор прямой
- направляющий вектор прямой ![]() . Теорема доказана.
. Теорема доказана.
Частные случаи общего уравнения прямой.
Если некоторые из коэффициентов уравнения (3.2.1) обращаются в нуль, то уравнение будет неполным, а в расположении прямой относительно координатных осей будут некоторые особенности.
1).
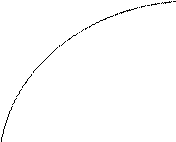
При с=0 прямая имеет уравнение ![]() . Эта прямая проходит
через начало координат.
. Эта прямая проходит
через начало координат.
2).
При а=0 уравнение прямой имеет вид 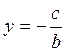 . Прямая параллельна оси
абсцисс.
. Прямая параллельна оси
абсцисс.
3).
При в=0 уравнение прямой имеет вид 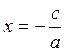 . Прямая параллельна оси
ординат.
. Прямая параллельна оси
ординат.
4). При а=с=0 получаем у=0. Это – ось абсцисс.
5). При в=с=о получаем х=0. Это – ось ординат.
Все эти случаи показаны на рис. 3.6.
Пример.
Найдите уравнения биссектрис углов между прямыми ![]() и
m:
и
m: ![]() .
.
Решение.
а) находим точку А пересечения данных прямых. Для этого решаем систему
уравнений 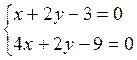 . В результате получаем А(2,
. В результате получаем А(2, ![]() ).
).
б)
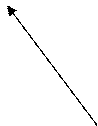
Теперь найдем направляющие векторы биссектрис. По доказанной выше теореме
векторы ![]() и
и ![]() являются
направляющими векторами данных прямых, см. рис. 3.7. Сравнивая длины этих
векторов (
являются
направляющими векторами данных прямых, см. рис. 3.7. Сравнивая длины этих
векторов (![]() ), видим, что длина вектора в 2 раза
больше длины вектора
), видим, что длина вектора в 2 раза
больше длины вектора ![]() :
: 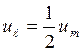 .
.
При сложении векторов по правилу параллелограмма, этот параллелограмм превращается в ромб, если слагаемые векторы имеют равные длины.
![]() Р2
Р2 ![]()
![]()
![]()
![]()
![]() m
m
![]()

![]()

![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()


![]()
![]()
![]() Р1
α
Р1
α
![]()
![]()

![]() А
А ![]()
![]()
![]()
![]()
Рис.
3.7 ![]()
![]()
Рис. 3.8
А так же диагональ ромба делит его углы пополам, то сумма таких векторов направлена по биссектрисе угла между слагаемыми векторами.
Поэтому
направляющие векторы ![]() и
и ![]() биссектрис
Р1 и Р2 таковы:
биссектрис
Р1 и Р2 таковы: 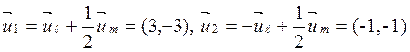 .
.
в)
Уравнения биссектрис находим по точке и направляющему вектору. Имеем: 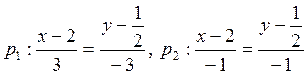 . После упрощений получаем окончательно:
. После упрощений получаем окончательно: ![]()
§ 3.3. Углы между прямыми. Параллельность и перпендикулярность
Две
прямые ![]() и
и ![]() ,
пересекаясь, образуют четыре угла, различными из которых могут быть только два
смежных: на рис. 3.8 они обозначены
,
пересекаясь, образуют четыре угла, различными из которых могут быть только два
смежных: на рис. 3.8 они обозначены ![]() и
и ![]() . Одни из этих углов равен углу между
нормальными векторами
. Одни из этих углов равен углу между
нормальными векторами ![]() и
и ![]() этих
прямых. В обозначениях того же рисунка
этих
прямых. В обозначениях того же рисунка ![]() , так
как
, так
как 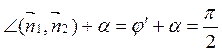 .
.
Задача.
Найти угол между прямыми ![]() и
и ![]() .
.
Решение.
Определяем угол ![]() как угол между векторами
как угол между векторами ![]() и
и ![]() по
формуле (2.7.10):
по
формуле (2.7.10): 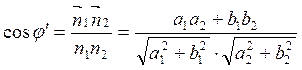 . Далее по формулам привидения
находим косинус второго угла
. Далее по формулам привидения
находим косинус второго угла ![]() :
: ![]() .
.
Окончательно. Введя для углов между прямыми общее обозначение φ, имеем:
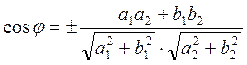 (3.3.1)
(3.3.1)
Задача
решена. Из полученной формулы можно вывести условия параллельности и
перпендикулярности прямых, но предпочтительней независимый вывод этих условий: 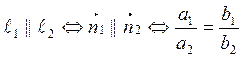 ,
,
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.